
0391_Чащин_Лр7
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физики
Лабораторная работа №7.(1)
по дисциплине «Физика»
Тема: ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЕЛ В ДИССИПАТИВНОЙ СРЕДЕ
Студент гр. 0391 |
Чащин Д. |
|
Преподаватель |
Шейнман И.Л. |
|
Санкт-Петербург
2020
Цель работы: определение вязкости диссипативной среды (жидкости) по установившейся скорости движения в ней шарика, а также исследование процессов рассеяния энергии в диссипативной среде.
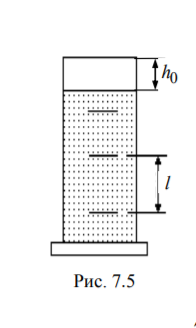
Приборы и принадлежности: цилиндрический сосуд с жидкостью(рис.7.5), металлические шарики, аналитические весы, масштабная линейка, секундомер.
Протокол наблюдений

Основные теоретические положения.
Сила трения направлена по касательной к поверхности соприкосновения слоев и описывается законом Ньютона.

Кинематическая вязкость.
![]()
Число Рейнольдса.
![]()
Определение силы сопротивления при Re<0.5 по формуле Стокса.
![]()
где коэффициент сопротивления при обтекании жидкостью жесткого шара равен
![]()
В случае турбулентного обтекания при Re > 150 сила сопротивления становится пропорциональной квадрату скорости:
![]() 6.
6.
6. При установившемся падении шарика в жидкости сила сопротивления уравновешивается силой тяжести и архимедовой силой:
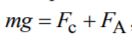
Если сила сопротивления определяется формулой Стокса, то формула для расчета скорости имеет вид:
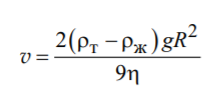 ,
а формула определения времени имеет
вид
,
а формула определения времени имеет
вид
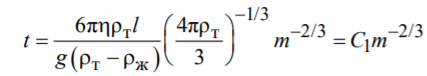 ,
из вышезаписанного уравнения может
быть найдена вязкость
,
из вышезаписанного уравнения может
быть найдена вязкость
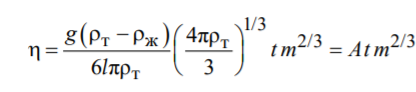
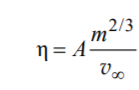
Когда сила сопротивления квадратично зависит от скорости, формулы для расчета времени и скорости:
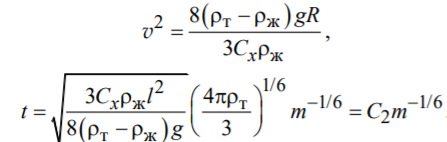
Зависимость v(t) и a(t) определяются как:
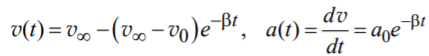 ,
где
,
где
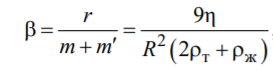
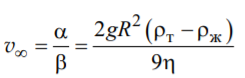
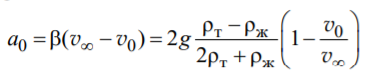
![]()
Временем релаксации процесса перехода движения тела от нестационарного режима к стационарному можно найти как:
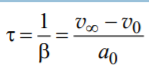
А – константа, зависящая от плотности жидкости и материала шарика:
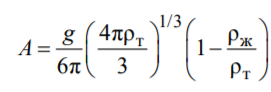
Полная механическая энергия движущегося в жидкости тела в произвольный момент времени определяется выражением:
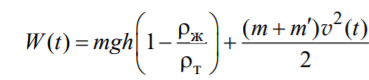
Скорость диссипации энергии (мощность потерь) в установившемся режиме может быть найдена как:
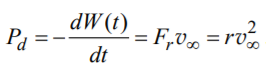
Количество теплоты, выделяющиеся за счет трения шарика о жидкость:
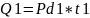
Вопросы
2. Дайте определения динамической, кинематической вязкости и текучести жидкости, а также ее ламинарного и турбулентного течения.
Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.
Текучесть – способность изменять форму за малое время под действием даже малых сил.
Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ и определяется формулой: ν = µ / ρ, где µ - динамическая вязкость, Па·с, ρ - плотность жидкости, кг/м³.
Ламинарное течение — течение, при котором жидкость перемещается слоями без перемешивания и пульсаций (то есть без беспорядочных быстрых изменений скорости и давления).
Турбулентное течение - форма течения жидкости, при которой ее элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущейся жидкости.
30. Напишите аналитическую формулу зависимости скорости движения тела от времени при движении в диссипативной среде в случае, когда начальная скорость нулевая.
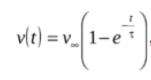 ,
где
τ – время релаксации, которое находится
по следующей формуле:
,
где
τ – время релаксации, которое находится
по следующей формуле:
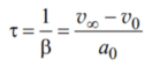
Обработка результатов
1.Сила сопротивления Fc , действующая со стороны жидкости на движущийся в ней со скоростью v шарик радиусом R, может при определенных условиях выражаться формулой:
![]()
При установившемся падении шарика в жидкости сила сопротивления уравновешивается силой тяжести и архимедовой силой:
![]() ,
где масса шарика
,
где масса шарика
![]() .
Тогда имеем равенство:
.
Тогда имеем равенство:
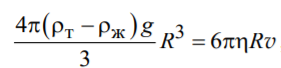
Выразим скорость:
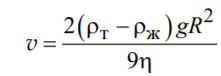
Установившаяся скорость может быть найдена как v=l/t.
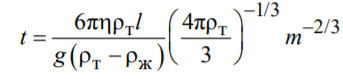
Выразим вязкость
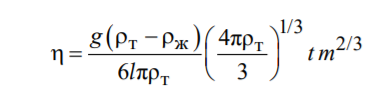
2. Построим графики зависимости ln t от ln m.
Расчеты времени при линейной зависимости силы сопротивления от скорости и значение ln m в опыте 1-10 (рис.2.1):

Рис.2.1
График зависимости ln t от ln m(рис.2.2) (сила сопротивления линейно зависит от скорости)
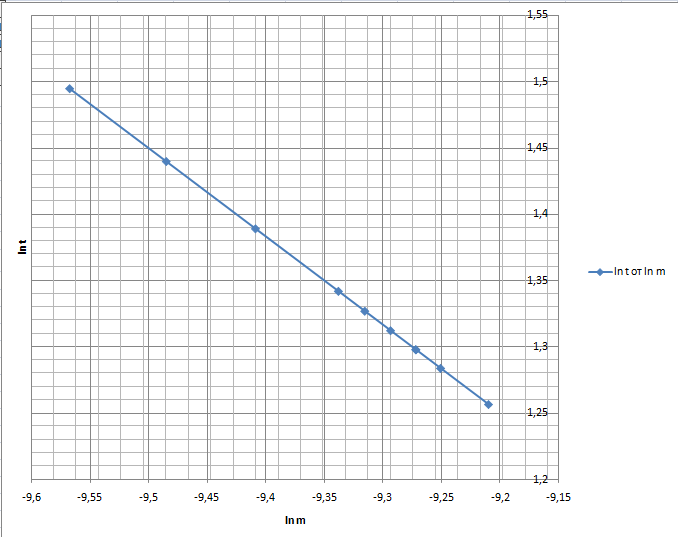
Рис.2.2
Расчеты времени при квадратичной зависимости силы сопротивления от скорости и значение ln m в опыте 1-10 (рис.2.3):

Рис.2.3
График зависимости ln t от ln m(рис.2.4) (сила сопротивления квадратично зависит от скорости)
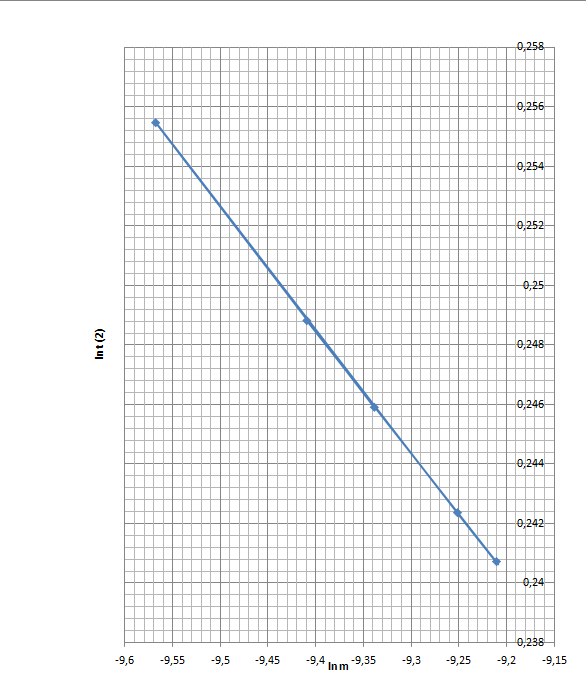
Рис.2.4
Найдем угловой коэффициент аппроксимирующей прямой(рис.2.5)
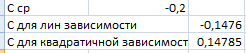
Рис.2.5
Вычислим константу
С=
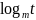 (рис.2.6), где t
и m
– данные с протокола, и сравним ее с
найденными угловыми коэффициентами.
(рис.2.6), где t
и m
– данные с протокола, и сравним ее с
найденными угловыми коэффициентами.
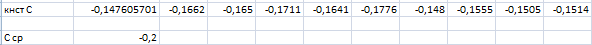
Рис.2.6
Т.к
данная константа (ее среднее значение)
рано угловому коэффициенту аппроксимирующей
прямой графика для линейной зависимости,
можно сделать вывод, что формула
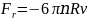 лучше описывает зависимость силы
сопротивления от скорости шариков.
лучше описывает зависимость силы
сопротивления от скорости шариков.
3. Определим константу С1(рис.3.1)
![]()
Рис.3.1
Выполним расчет значения коэффициента вязкости(рис.3.2).
![]()
Рис.3.2
4. Для каждого из диаметров шариков рассчитаем число Рейнольдса (рис.4.1) и сделаем вывод о характере обтекания при падении шарика в жидкости.

Рис.4.1
Число Рейнольдса < 0,5, значит, для коэффициента сопротивления движению шара можно применять Формулу Стокса.
Полученные результаты и выводы пункта 4 совпадают с заключением пункта 2.
5. Рассчитаем константу А в формуле для расчета вязкости жидкости (рис.5.1).
![]()
Рис.5.1
Определим значения вязкости жидкости c 95 %P выборочным методом(рис.5.2).
Выполним проверку на промахи:
Коэффициент
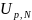 ,
для проверки результатов наблюдений
на наличие грубых погрешностей в
зависимости от объема выборки N=5 для
доверительной вероятности Р = 95 %, равен
=0,64.
,
для проверки результатов наблюдений
на наличие грубых погрешностей в
зависимости от объема выборки N=5 для
доверительной вероятности Р = 95 %, равен
=0,64.
Критерий отсутствия
промахов:

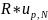 =0,64*0,116=0,07
=0,64*0,116=0,07
Выполнение условия
и значения
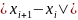 :
:
![]()
Заключение: промахов нет.
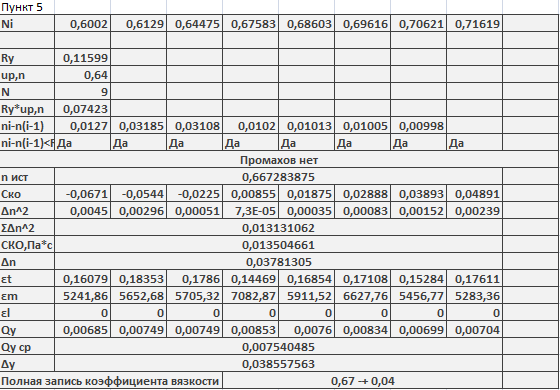
Рис.5.2
 0, 67
0, 67
 0,04 Па*с
0,04 Па*с
Полученное значение коэффициента вязкости с учетом погрешности совпадает с найденным в предыдущем пункте.
6. Рассчитаем для первого опыта начальные скорость, ускорение и время релаксации(рис.6.1).
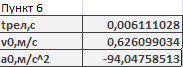
Рис.6.1
Построим графики зависимостей v=v(t) и a=a(t).
Данные для построения a(t).(рис.6.2)
![]()
Рис.6.2
График a(t) (рис.6.3)
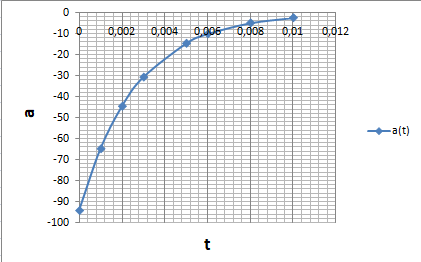
Рис.6.3
Данные для построения v(t). (рис.6.4)
![]()
Рис.6.4
График v(t) (рис.6.5)
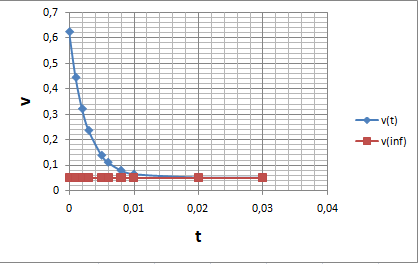
Рис.6.5
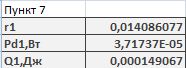
7.Вычислим количество теплоты Q1, выделяющееся за счет трения шарика о жидкость, при его прохождении между двумя метками(рис.7.1).
8. Полученное экспериментальным путем значение коэффициента вязкости: 0,67 0,04.
Табличное значение вязкости: 1,48

Вывод: наблюдая за прохождением шарика пути между двумя метками в жидкости, мы могли изучить свойства диссипативной среды, экспериментально определили значение вязкости среды, исследовали процессы рассеяния энергии в диссипативной среде.
