Контрольные / Маслов / 3 сем Маслов КР 1

Электростатика Вариант № 1

1. Найти дипольный момент системы зарядов с объемной плотностью в сферической системе координат

2. Две бесконечные параллельные проводящие плиты заряжены так, что суммарная поверхностная плотность заряда одной из плит равна ₁, а другой ₂. Найти плотность заряда каждой поверхности обеих плит.

3. Три одинаковых шарика массой m каждый заряжены одинаковыми зарядами q и связаны тремя одинаковыми нитями так, что образуют правильный треугольник со стороной a. Одну из нитей пережигают. Определить максимальную скорость среднего шарика. Внешними силами пренебречь.

Э лектростатика Вариант № 2

1. Найти разность потенциалов между точками A и B, создаваемую двумя бесконечными плоскими взаимно перпендикулярными равномерно заряженными поверхностями (см. рис.). Поверхностные плотности заряда равны: ₁ = 210^–7 Кл/м², ₂ = 4,210^–7 Кл/м². a = 7 см, b = 5 см.

2. Найти емкость цилиндрического конденсатора длины L с радиусами обкладок a и b, левая половина которого заполнена диэлектриком с постоянной проницаемостью ₁, а правая – диэлектриком с постоянной проницаемостью ₂.

3. Эбонитовый шар (=2,7) равномерно заряжен по объему. Во сколько раз энергия электрического поля вне шара превосходит энергию поля, сосредоточенную в шаре?

Электростатика Вариант № 3

1 . В бесконечном плоском слое толщины h вырезана сферическая полость диаметром h (рис.). Определить напряженность электрического поля в точках A и B, если слой равномерно заряжен с объемной плотностью заряда .

2. Металлическая сфера радиусом R₁, заряженная зарядом q, окружена сферическим концентрическим слоем диэлектрика с диэлектрической проницаемостью . Радиусы внутренней и внешней поверхностей слоя равны R₂ и R₃. Найти зависимости напряженности и потенциала электрического поля от расстояния до центра системы.

_{3. Найти энергию заряда q, расположенного в начале координат, если диэлектрическая проницаемость среды}

Электростатика Вариант № 4

1. Найти плотность электрического заряда в атмосфере, если на поверхности Земли напряженность электрического поля равна E₁ = 100 В/м, а на высоте h = 1,5 км – Е₂ = 25 В/м. Считать, что плотность заряда постоянна, а вектор напряженности направлен вертикально вверх.

2 . Точечный заряд q находится в центре сферического слоя диэлектрика с диэлектрической проницаемостью  (рис.). Какую работу надо совершить, чтобы удалить заряд через узкий канал из центра на бесконечность? Внутренний и наружный радиусы слоя равны r и R.

3. Между пластинами плоского конденсатора находится пластина диэлектрика с проницаемостью . Емкость конденсатора C, его заряд q. Какую работу надо совершить, чтобы вытащить пластину из конденсатора? Трения нет, конденсатор отключен от источника напряжения.

Электростатика Вариант № 5

1. Две концентрические сферы находятся одна в другой. Внутреннюю сферу нагрели, и она начала излучать электроны. В секунду вылетает n электронов со скоростью v. Через какое время заряды сфер перестанут изменяться, если радиус внутренней сферы равен r, а радиус внешней на r больше. r << r.

2. Восемь протонов находятся в вершинах куба с ребром l = 10 см. Какова будет их максимальная скорость, если предоставить им возможность свободно двигаться?

3 . С какой силой втягивается диэлектрическая пластина в плоский конденсатор, заряженный зарядом q? Диэлектрическая проницаемость пластины , ее толщина d равна расстоянию между пластинами конденсатора, размеры всех трех пластин a  b, пластина вдвинута в конденсатор на величину x (рис.). Силы трения нет.

Э лектростатика Вариант № 6

1. Две бесконечные плоские параллельные поверхности заряжены равномерно с одинаковой поверхностью заряда . Найти разность потенциалов между точками A и B (рис.). Геометрические размеры указаны на рисунке.

2. Металлический шар радиусом R₁, заряженный до потенциала ₁ окружают тонкой сферической концентрической металлической оболочкой радиусом R₂. Каким будет потенциал шара, если его соединить с оболочкой проволокой?

3. Заряженное тело сжали так, что все его размеры уменьшились в n раз. Во сколько раз изменилась энергия электрического поля этого тела?

Э лектростатика Вариант № 7

1. Две бесконечные плоские равномерно заряженные параллельные пластины дают напряженности электрического поля в точках A и B E_A и E_B соответственно (рис.). Найти поверхностные плотности зарядов пластин ₁ и ₂.

2. Металлический шар радиусом R₁ окружен сферическим слоем диэлектрика с диэлектрической проницаемостью . Внутренний радиус диэлектрика равен R₁, а внешний – R₂. Шар заряжен зарядом q. Найти потенциал шара и связанные заряды, наведенные на поверхностях диэлектрика.

3. Между пластинами плоского конденсатора находится пластина диэлектрика с проницаемостью . Емкость конденсатора C, его заряд q. Какую работу надо совершить, чтобы вытащить пластину из конденсатора? Трения нет, конденсатор отключен от источника напряжения.

Электростатика Вариант № 8

1 . Плоский бесконечный слой толщиной h равномерно заряжен по объему с объемной плотностью заряда =cos(πx/h) (рис.). Определить зависимость напряженности электрического поля в зависимости от расстояния x до среднего сечения слоя.

2. Проводник заряжен электрическим зарядом. Определить давление, которое испытывает поверхность проводника со стороны электрического поля в точке с поверхностной плотностью заряда .

3. Электрическое поле создано длинным металлическим цилиндром, имеющим линейную плотность заряда 1 мкКл/м.

Найти: а) энергию электрического поля, заключенную в объеме диэлектрика с проницаемостью, равной 4.5, ограниченную этим цилиндром и коаксиальной с ним цилиндрической поверхностью в 4 раза большего радиуса и длиной 1 м;

б) плотность зарядов, индуцированных на поверхностях диэлектрика.

Электростатика Вариант № 9

1. Бесконечно длинный цилиндр радиусом R заряжен электрическим зарядом с объемной плотностью ρ = Cr³ где C=const. Определить напряженность электрического поля внутри и снаружи.

2. Точечный диполь с моментом p на расстоянии l от проводящей плоскости. Найти силу, действующую на диполь, если вектор p параллелен плоскости.

3. Между пластинами плоского конденсатора находится пластина диэлектрика с проницаемостью . Емкость конденсатора C, его заряд q. Какую работу надо совершить, чтобы вытащить пластину из конденсатора? Трения нет, конденсатор не отключен от источника напряжения.

Электростатика Вариант № 10

1. Бесконечная тонкая плоская поверхность, заряжена с поверхностной плотностью заряда , где C=const, а r –расстояние от точки O, лежащей на поверхности. Определить напряженность электрического поля в точке, лежащей на перпендикуляре с основанием в точке O, на расстоянии a от поверхности.

2. Одну пластину незаряженного конденсатора емкостью C заземляют, а другую присоединяют длинным проводом к удаленному металлическому шару радиусом r, имеющему заряд q_o. Какой заряд останется на шаре?

3. Электрическое поле создано металлической сферой радиуса 18 см, имеющей поверхностную плотность заряда 2 мкКл/м².

Найти: а) энергию электрического поля, заключенную в объеме диэлектрика с проницаемостью, равной 2, ограниченную этой сферой и концентрической с ней сферической поверхностью в 2 раза большего радиуса;

б) плотность зарядов, индуцированных на поверхности диэлектрика.

Электростатика Вариант № 11

1. Шар радиусом R заряжен по объему с объемной плотностью заряда =Cr³ где C=const. Определить напряженность и потенциал электрического поля внутри шара и снаружи.

2. Металлический шар радиусом R₁ заряженный до потенциала , окружают тонкой сферической концентрической оболочкой радиусом R₂. Каким будет потенциал шара, если оболочку заземлить?

3 . С какой силой втягивается диэлектрическая пластина в плоский конденсатор, заряженный зарядом q? Диэлектрическая проницаемость пластины , ее толщина d равна расстоянию между пластинами конденсатора, размеры всех трех пластин a  b, пластина вдвинута в конденсатор на величину x (рис.). Силы трения нет.

Электростатика Вариант № 12

1 . Электрическое поле образовано внешним однородным электрическим полем и полем заряженной металлической пластины. Напряженность результирующего поля равна (рис.): E₁ = 30 кВ/м, E₂ = 50 кВ/м. Определить заряд пластины, если сила, действующая не нее со стороны поля равна F = 0,7 Н.

2. Два металлических шарика радиусами r₁ и r₂ заряжены до потенциалов ₁ и ₂ и находятся на большом расстоянии друг от друга. Каким будет потенциал шариков, если соединить их тонкой проволокой?

_{3. Система состоит из двух концентрических тонких металлических оболочек с радиусами R1 и R2 и соответствующими зарядами q1 и q2. Найти собственную энергию W1 и W2 каждой оболочки, энергию взаимодействия W12 оболочек и полную электрическую энергию W системы.}

Электростатика Вариант № 13

1. Найти напряженность электрического поля в центре сферы, создаваемую зарядами, равномерно распределенными с поверхностной плотностью  по четверти сферы 0<φ<π, 0<θ<π/2.

2 . Между замкнутыми пластинами плоского конденсатора находится металлическая пластина с зарядом q. Размеры всех трех пластин одинаковы и все они параллельны. Внутреннюю пластину переместили параллельно самой себе на расстояние x (рис.). Какой заряд прошел по проводу замыкания? Расстояние между пластинами конденсатора равно d.

3. Два длинных прямых провода одинакового радиуса сечения a расположены в диэлектрике с проницаемостью . Расстояние между их осями равно b. Найти емкость системы на единицу длины при условии a<<b.

Электростатика Вариант № 14

1 . Квадрат составлен из четырех одинаково и равномерно заряженных стержней (рис.). Если убрать стержень AB, то напряженность электрического поля в центре квадрата станет равна E. Какой станет напряженность в центре квадрата, если убрать еще и стержень BC?

2 . Четыре одинаковые металлические пластаны площадью S = 220 см² расположены на расстоянии d = 1 мм друг от друга и соединены как показано на рис. Найти емкость такой системы.

_{3. Внутри плоского конденсатора находится параллельная обкладкам рластина толщиной =1/2 расстояния между обкладками. Емкость конденсатора в отсутствие пластины C=100 нФ. Конденсатор сначала подключают к источнику посоянного напряжения U=300 В, затем отключают и медлеено извлекают пластину из зазора. Найти работу, совершенную против электрических сил при извлечении пластины, если она металлическая.}

Электростатика Вариант № 15

1 . Три квадратные одинаково и равномерно заряженные пластины из диэлектрика сложены вместе (рис.). При этом в некоторой точке T, расположенной над общей точкой, напряженность электрического поля равна E₁. Когда пластину A убрали, напряженность в этой точке стала равна E₂. Какой станет напряженность в точке T, если убрать и пластину B?

_{2. Определить поляризацию, электрическое поле, электрическое смещение и плотность поляризационных зарядов на поверхностях слюдяной пластинки толщиной d=0.2 мм, служащей изолятором в плоском конденсаторе, заряженном до напряжения 400 В.}

_{3. В центре сферической оболочки, равномерно заряженной зарядом q=5 мкКл, расположен точечный заряд q0=1,5 мкКл. Найти работу электрических сил при увеличении радиуса оболочки от R1= 50 мм до R2= 100 мм.}

Электростатика Вариант № 16

1 . Диполь, состоящий из двух точечных зарядов +q и –q массой m каждый, движется из бесконечности вдоль осевой линии плоского конденсатора (рис.). Расстояние между пластинами конденсатора d, расстояние между зарядами диполя l (l < d). Между пластинами конденсатора поддерживается постоянная разность потенциалов . Какова скорость диполя внутри конденсатора, если на бесконечности она равна ?

_{2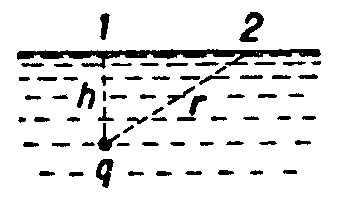 . В керосине на глубине h = 3 см от свободной поверхности находится точечный заряд q = 1.7 нКл (см. рис.). Определить плотность поляризационных зарядов на поверхности керосина:}

_{а) над зарядом;}

_{б) на расстоянии r = 5 см от заряда;}

_{в) определить полную величину поляризационного заряда на поверхности керосина.}

_{3. В цилиндрический конденсатор вводят длинный цилиндрический слой диэлектрика проницаемости , заполняющий практически весь зазор между обкладками. Средний радиус обкладок R, зазор между ними d, причем d << R. Обкладки конденсатора подключены к источнику напряжения U. Найти модуль электрической силы, втягивающей диэлектрик в конденсатор.}

Электростатика Вариант № 17

1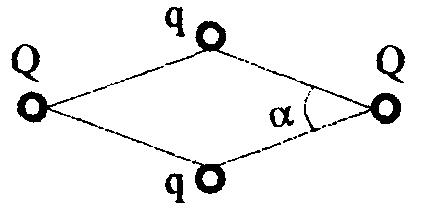 . Четыре положительных заряда q и Q связаны четырьмя одинаковыми нитями (рис.). Определить угол между нитями при вершине Q. Внешними силами пренебречь.

_{2. Две горизонтально расположенные пластинки площадью S = 300 см}² _{несут противоположные по знаку заряды, равные по модулю q = 0.2 мкКл. Пластины расположены так близко, что поле между ними можно считать однородным. Нижняя пластина погружена в жидкий диэлектрик с диэлектрической проницаемостью  = 3. Определить силы, действующие на каждую из пластин и поверхность жидкости.}

_{3. Внутри плоского конденсатора находится параллельная обкладкам пластина толщиной =1/2 расстояния между обкладками. Емкость конденсатора в отсутствие пластины C=100 нФ. Конденсатор сначала подключают к источнику постоянного напряжения U=300 В, затем отключают и медленно извлекают пластину из зазора. Найти работу, совершенную против электрических сил при извлечении пластины, если она фарфоровая.}

Электростатика Вариант № 18

1. По тонкой нити, изогнутой по дуге окружности радиусом R, равномерно распределен заряд с линейной плотностью =10 нКл/м. Определить напряженность Е и потенциал  электрического поля, создаваемого таким распределенным зарядом в точке О, совпадающей с центром кривизны дуги. Длина l нити составляет 1/3 длины окружности и равна 15 см.

2. Небольшое облако с зарядом q = 20 Кл находится на высоте h = 1 км рад поверхностью Земли. Считая Землю проводником, определить напряженность поля, создаваемого этим зарядом на расстоянии s = 3 км от места над которым находится заряд, а также полный заряд, индуцированный облаком. Кривизной поверхности Земли пренебречь.

_{3. В цилиндрический конденсатор вводят длинный цилиндрический слой диэлектрика проницаемости , заполняющий практически весь зазор между обкладками. Средний радиус обкладок R, зазор между ними d, причем d<< R. Заряд конденсатора постоянен и равен Q. Найти модуль электрической силы, втягивающей диэлектрик в конденсатор если длина конденсатора H, а диэлектрик вставлен на длину x.}

Электростатика Вариант № 19

1 . На плоский слой, заряженный равномерно по объему положительным зарядом с плотностью  (см. рис.), падают положительно заряженные частицы с зарядом q и кинетической энергией W. Определить толщину слоя, если известно, что максимальный угол падения, при котором частицы могут пролететь слой, равен .

2. Два проводника находятся на большом расстоянии друг от друга. Первый, емкостью C₁ = 10^–5 мкФ, заряжен до потенциала ₁ = 6 кВ, а второй, емкостью C₂ = 210^–5 мкФ – до ₂ = 12 кВ. Какое количество теплоты выделится, если соединить проводники тонкой проволокой?

3. Два одинаковых шара находятся на большом расстоянии друг от друга. Поле первого шара имеет энергию W₁ = 1610^–4 Дж, а второго – W₂ = 3610^–4 Дж. Какое количество теплоты выделится при соединении этих шаров тонкой проволокой?

Электростатика Вариант № 20

1. Найти плотность электрического заряда в атмосфере, если на поверхности Земли напряженность электрического поля равна E₁ = 100 В/м, а на высоте h = 1,5 км – Е₂ = 25 В/м. Считать, что плотность заряда постоянна, а вектор напряженности направлен вертикально вверх.

2. Восемь протонов находятся в вершинах куба с ребром l = 10 см. Какова будет их максимальная скорость, если предоставить им возможность свободно двигаться?

3. Заряженное тело сжали так, что все его размеры уменьшились в n раз. Во сколько раз изменилась энергия электрического поля этого тела?

Э лектростатика Вариант № 21

1. Две бесконечные плоские равномерно заряженные параллельные пластины дают напряженности электрического поля в точках A и B E_A и E_B соответственно (рис.). Найти поверхностные плотности зарядов пластин ₁ и ₂.

2. Проводник заряжен электрическим зарядом. Определить давление, которое испытывает поверхность проводника со стороны электрического поля в точке с поверхностной плотностью заряда .

3. Между пластинами плоского конденсатора находится пластина диэлектрика с проницаемостью . Емкость конденсатора C, его заряд q. Какую работу надо совершить, чтобы вытащить пластину из конденсатора? Трения нет, конденсатор не отключен от источника напряжения.

Электростатика Вариант № 22

1. Бесконечная тонкая плоская поверхность, заряжена с поверхностной плотностью заряда , где C=const, а r –расстояние от точки O, лежащей на поверхности. Определить напряженность электрического поля в точке, лежащей на перпендикуляре с основанием в точке O, на расстоянии a от поверхности.

2. Металлический шар радиусом R₁ заряженный до потенциала , окружают тонкой сферической концентрической оболочкой радиусом R₂. Каким будет потенциал шара, если оболочку заземлить?

_{3. Система состоит из двух концентрических тонких металлических оболочек с радиусами R1 и R2 и соответствующими зарядами q1 и q2. Найти собственную энергию W1 и W2 каждой оболочки, энергию взаимодействия W12 оболочек и полную электрическую энергию W системы.}

Электростатика Вариант № 23

1. Найти напряженность электрического поля в центре сферы, создаваемую зарядами, равномерно распределенными с поверхностной плотностью  по четверти сферы 0<φ<π, 0<θ<π/2.

2 . Четыре одинаковые металлические пластаны площадью S = 220 см² расположены на расстоянии d = 1 мм друг от друга и соединены как показано на рис. Найти емкость такой системы.

_{3. В центре сферической оболочки, равномерно заряженной зарядом q=5 мкКл, расположен точечный заряд q0=1,5 мкКл. Найти работу электрических сил при увеличении радиуса оболочки от R1= 50 мм до R2= 100 мм.}

Электростатика Вариант № 24

1 . Диполь, состоящий из двух точечных зарядов +q и –q массой m каждый, движется из бесконечности вдоль осевой линии плоского конденсатора (рис.). Расстояние между пластинами конденсатора d, расстояние между зарядами диполя l (l < d). Между пластинами конденсатора поддерживается постоянная разность потенциалов . Какова скорость диполя внутри конденсатора, если на бесконечности она равна ?

_{2. Две горизонтально расположенные пластинки площадью S = 300 см}² _{несут противоположные по знаку заряды, равные по модулю q = 0.2 мкКл. Пластины расположены так близко, что поле между ними можно считать однородным. Нижняя пластина погружена в жидкий диэлектрик с диэлектрической проницаемостью  = 3. Определить силы, действующие на каждую из пластин и поверхность жидкости.}

_{3. В цилиндрический конденсатор вводят длинный цилиндрический слой диэлектрика проницаемости , заполняющий практически весь зазор между обкладками. Средний радиус обкладок R, зазор между ними d, причем d<< R. Заряд конденсатора постоянен и равен Q. Найти модуль электрической силы, втягивающей диэлектрик в конденсатор если длина конденсатора H, а диэлектрик вставлен на длину x.}

Э лектростатика Вариант № 25

1. Найти разность потенциалов между точками A и B, создаваемую двумя бесконечными плоскими взаимно перпендикулярными равномерно заряженными поверхностями (см. рис.). Поверхностные плотности заряда равны: ₁ = 210^–7 Кл/м², ₂ = 4,210^–7 Кл/м². a = 7 см, b = 5 см.

2. Металлическая сфера радиусом R₁, заряженная зарядом q, окружена сферическим концентрическим слоем диэлектрика с диэлектрической проницаемостью . Радиусы внутренней и внешней поверхностей слоя равны R₂ и R₃. Найти зависимости напряженности и потенциала электрического поля от расстояния до центра системы.

3. Между пластинами плоского конденсатора находится пластина диэлектрика с проницаемостью . Емкость конденсатора C, его заряд q. Какую работу надо совершить, чтобы вытащить пластину из конденсатора? Трения нет, конденсатор отключен от источника напряжения.

Электростатика Вариант № 26

1. Две концентрические сферы находятся одна в другой. Внутреннюю сферу нагрели, и она начала излучать электроны. В секунду вылетает n электронов со скоростью v. Через какое время заряды сфер перестанут изменяться, если радиус внутренней сферы равен r, а радиус внешней на r больше. r << r.

2. Металлический шар радиусом R₁, заряженный до потенциала ₁ окружают тонкой сферической концентрической металлической оболочкой радиусом R₂. Каким будет потенциал шара, если его соединить с оболочкой проволокой?