Контрольные / Маслов / 3 сем маслов КР 2

Электродинамика. Ток Вариант № 1

1. Пластины плоского конденсатора имеют форму квадратов со стороной a = 21 см. Расстояние между пластинами составляет d = 2 мм. Конденсатор присоединен к полюсам источника постоянного напряжения U = 750 В. В пространство между пластинами с постоянной скоростью v = 8 см/с вдвигают стеклянную пластинку толщины d = 2 мм. Какой силы ток I пойдет при этом по цепи? Диэлектрическая проницаемость стекла  = 7.

2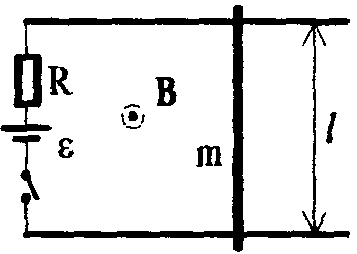 . Две параллельные проводящие рейки расположены в горизонтальной плоскости на расстоянии l друг от друга. Рейки подключены к источнику с ЭДС  через ключ и резистор с сопротивлением R (рис.). По рейкам перпендикулярно им может двигаться проводящая перемычка массой m. Вся система находится в однородном вертикальном магнитном поле с индукцией B. Ключ замыкают. Найти начальное ускорение перемычки и ее максимальную установившуюся скорость движения, если коэффициент трения равен . Сопротивлением всех остальных элементов кроме R пренебречь.

3. Заряженный и отключенный от источника питания плоский конденсатор с круглыми пластинами радиуса R пробивается электрической искрой вдоль своей оси. Считая разряд квазистационарным и пренебрегая краевыми эффектами, вычислить мгновенное значение плотности тока смещения j_см, считая ее независящей от r и магнитного поля H внутри конденсатора как функцию r, где r – расстояния от его оси. Сила тока в искре в рассматриваемый момент равна I.

Э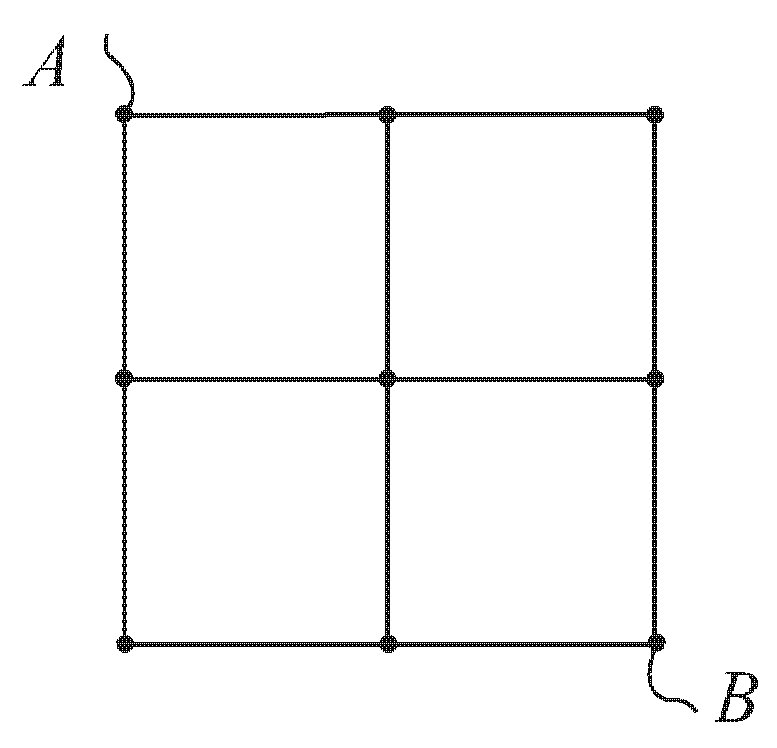 лектродинамика. Ток Вариант № 2

1 В схеме, изображенной на рисунке, определите сопротивление R_AB цепи между точками A и В, если сопротивление каждого звена r.

2. Найти ЭДС индукции, возникающую в бесконечном прямом проводе, если в контуре в виде прямоугольного треугольника течет ток I. Вершина прямого угла лежит на проводе, а гипотенуза параллельна проводу.

3. Пространство внутри длинного соленоида, состоящего из N витков проволоки, заполнено однородным веществом с диэлектрической магнитной проницаемостью  и . Длина соленоида равно l, радиус – R. По обмотке соленоида течет переменный ток силой . Вычислить электрическую и магнитную энергии, локализованные внутри соленоида.

Электродинамика. Ток Вариант № 3

1. Из куска проволоки, имеющей сопротивление R_o = 32 Ом, изготовлено кольцо. К двум точкам этого кольца присоединены подводящие ток провода. а) В каком отношении делят точки присоединения длину окружности кольца, если общее сопротивление получившейся цепи R = 6 Ом? б) Какова максимально возможная величина общего сопротивления R_max между двумя точками проволочного кольца?

2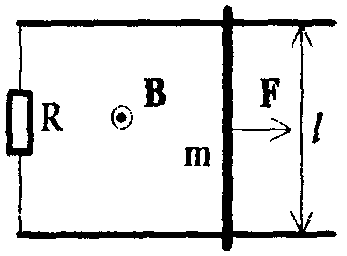 . Две параллельные проводящие рейки расположены в горизонтальной плоскости на расстоянии l друг от друга. По ним без трения может двигаться легкая проводящая перемычка. Рейки соединены друг с другом через резистор с сопротивлением R. Система находится в вертикальном однородном магнитном поле с индукцией B (рис.). Перемычку тянут вдоль реек. Какую горизонтальную силу надо прикладывать к перемычке, чтобы в сопротивлении выделялась постоянная мощность N?

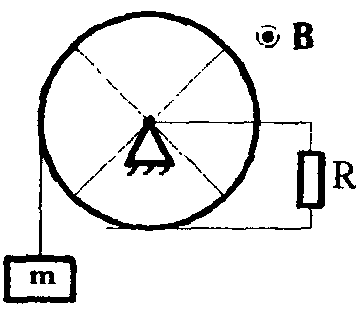
3. Медное кольцо радиусом r соединено проводящими спицами с центром. К центру и кольцу подключен резистор сопротивлением R. На кольцо намотана нить с грузом массой m. Кольцо вращается без трения вокруг оси, проходящей через его центр и находится в однородном магнитном поле с индукцией B, направленной параллельно его оси (рис.). Найти установившуюся скорость опускания груза.

Э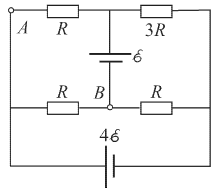 лектродинамика. Ток Вариант № 4

1. В схеме на рисунке внутренние сопротивления источников пренебрежимо малы. Определите силу тока I₁ через резистор сопротивления 3R, силу тока I₂ через источник тока с ЭДС 4ε и разность потенциалов U_AB между точками A и B схемы.

2. На пластины плоского конденсатора подано напряжение U. Отрицательная пластина конденсатора подогрета и излучает электроны, которые вылетают из нее практически без начальной скорости. Между пластинами конденсатора создано однородное магнитное поле, направленное параллельно пластинам. При какой наименьшей величине индукции магнитного поля тока в конденсаторе не будет? Расстояние между пластинами d.

3. В проводнике с проводимостью , помещенном в нестационарное магнитное поле, циркулируют токи Фуко 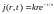. Линии тока представляют собой окружности, центры которых лежат на оси Oz. Определить магнитную индукцию в проводнике, если известно, что в момент времени она была равна нулю во всем объеме проводника.

Электродинамика. Ток Вариант № 5

1 . Определите сопротивление R между точками A и D (см. рис.) Сопротивления резисторов одинаковы и равны r. Сопротивлением соединяющих проводов можно пренебречь.

2. Найти силу взаимодействия между бесконечно длинным тонким прямолинейным проводом, по которому течет ток I₁ и отрезком прямого тонкого проводника длиной l с током I₂, лежащими в одной плоскости. Угол между проводниками равен , ближайший конец отрезка находится на расстоянии a от бесконечного провода.

3. Заряженный до напряжения U₀ и отключенный от источника плоский конденсатор с круглыми пластинами радиуса R медленно разряжается токами, возникающими в диэлектрике из-за наличия слабой проводимости . Пренебрегая краевыми эффектами, вычислите магнитное поле внутри конденсатора.

Электродинамика. Ток Вариант № 6

1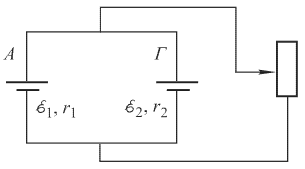 . Источниками электрического тока в системе электрического оборудования автомобиля являются генератор Г постоянного тока и соединенный с ним параллельно аккумулятор A (см. рис.). ЭДС аккумулятора ε₁ = 12 В, его внутреннее сопротивление r₁ = 0,15 Ом. ЭДС генератора ε₂ = 14 В, его внутреннее сопротивление r₂ = 0,05 Ом. Найдите зависимость силы тока I_A, протекающего через аккумулятор, от силы тока I_Н, потребляемого нагрузкой – переменным сопротивлением. Определите при каких значениях силы тока нагрузки I_Н аккумулятор будет заряжаться, а при каких – разряжаться.

2. Шар радиуса R, заряженный равномерно по объему зарядом q, вращается вокруг своей оси с постоянной угловой скоростью . Найти величину и направление магнитного момента шара.

3. Найдите направление и плотность тока смещения j_см в плоском конденсаторе, пластины которого раздвигаются со скоростью , оставаясь параллельными друг другу если: а)заряды на пластинах конденсатора остаются постоянными; б)разность потенциалов U остается постоянной. Расстояние между пластинами остается малым в сравнении с линейными размерами пластин.

Электродинамика. Ток Вариант № 7

1 . Определите сопротивление R между точками A и D (см. рис.). Сопротивления резисторов одинаковы и равны r. Сопротивлением соединяющих проводов можно пренебречь.

2. По бесконечной прямолинейной тонкой полосе шириной l течет постоянный поверхностный ток i. Найти величину и направление индукции магнитного поля в точке, находящейся на расстоянии h от полосы над ее серединой.

3. Ось катушки, имеющей N = 1000 витков, диаметром d = 10 см, расположена горизонтально по магнитному меридиану. По катушке течет ток I = 0.5 А. Горизонтальная составляющая магнитного поля Земли H = 16 А/м. Какую работу нужно совершить, чтобы повернуть катушку на 180?

Электродинамика. Ток Вариант № 8

1 . Каждый из отрезков проволочной конструкции (см. рис.) имеет одинаковое сопротивление r. Ток, протекающий по отрезку DF, равен i. Определите разность потенциалов U между узлами A и B, сопротивление R между этими узлами и полный ток I от A к B.

2. Определить индукцию магнитного поля B внутри бесконечной цилиндрической полости, сделанной в бесконечном цилиндрическом проводе, по которому течет ток с плотностью j, равномерно распределенной по сечению провода. Ось полости получается из оси провода параллельным переносом на вектор a.

3. На катушку, сопротивлением R = 10 Ом и индуктивностью L = 58 мГн подается постоянное напряжение. Через сколько времени ток в катушке достигнет величины, равной половине установившегося тока?

Электродинамика. Ток Вариант № 9

1 . Три одинаковых источника с ЭДС ε = 1,6 В и внутренним сопротивлением r включены в электрическую цепь по схеме, изображенной на рис. Миллиамперметр показывает ток I = 100 мА. Сопротивления резисторов R₁ = 10 Ом и R₂ = 15 Ом, сопротивление резистора R неизвестно. Какое напряжение U показывает вольтметр? Сопротивление вольтметра считать очень большим.

2. Найти ЭДС индукции, возникающую в бесконечном прямом проводе, если он расположен вдоль оси тороида прямоугольного сечения, на который равномерно намотана катушка, содержащая N=500 витков. Внутренний радиус тороида a = 4 см, внешний – b = 10.8 см, высота тороида h = 6 см, магнитная проницаемость материала –  =1000, в катушке течет ток I = I₀cost, I₀= 1 A.

3. Медный цилиндр радиусом r = 1 см и высотой h = 10 см помещен в переменное однородное магнитное поле с индукцией 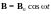, параллельное оси цилиндра. Амплитуда поля 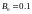Тл, частота f = 50 Гц. Определить среднюю тепловую мощность P, выделяемую в цилиндре из-за токов Фуко.

Э лектродинамика. Ток Вариант № 10

1. Каждый из отрезков двух проволочных конструкций (см. рисунок) имеет одинаковое сопротивление r. Ток, протекающий по отрезку DF, равен i. Определите разность потенциалов U между узлами A и B, сопротивление R между этими узлами и полный ток I от A к B.

2. Соленоид имеет N = 500 витков и обладает сопротивлением R = 5 Ом. Площадь поперечного сечения соленоида равна S = 10 см². Концы соленоида замыкают и вносят его в однородное магнитное поле с индукцией B = 10 мТл, силовые линии которого направлены под углом  = 60 к оси соленоида. Найти заряд, протекший через обмотку соленоида.

3. Заряженный и отключенный от источника питания плоский конденсатор с круглыми пластинами радиуса R пробивается электрической искрой вдоль своей оси. Считая разряд квазистационарным и пренебрегая краевыми эффектами, вычислить мгновенное значение плотности тока смещения j_см, считая ее независящей от r и магнитного поля H внутри конденсатора как функцию r, где r – расстояния от его оси. Сила тока в искре в рассматриваемый момент равна I.

Электродинамика. Ток Вариант № 11

1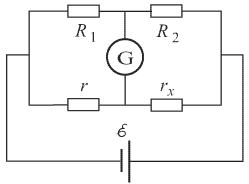 . В мосте Уитстона (см. рис.) сопротивления подбирают таким образом, что чувствительный гальванометр показывает нуль.

а) Считая сопротивления R₁, R₂ и r известными, определите величину сопротивления r_x.

б) Если поменять местами батарею и гальванометр, то снова получится мостовая схема. Сохранится ли баланс в новой схеме?

2. По бесконечной прямолинейной тонкой полосе шириной l течет постоянный поверхностный ток i. Найти величину и направление индукции магнитного поля в точке, находящейся на расстоянии h от полосы над ее серединой.

3. Пространство внутри длинного соленоида, состоящего из N витков проволоки, заполнено однородным веществом с диэлектрической магнитной проницаемостью  и . Длина соленоида равно l, радиус – R. По обмотке соленоида течет переменный ток силой . Вычислить электрическую и магнитную энергии, локализованные внутри соленоида.

Электродинамика. Ток Вариант № 12

1 . Найдите полное сопротивление R между точками A и B бесконечной цепи (см. рис.), состоящей из одинаковых резисторов сопротивлением r каждый.

2. Тонкий тороидальный сердечник составлен из двух половинок, сделанных из различных ферромагнитных материалов с магнитными проницаемостями ₁ и ₂. Общая длина сердечника, включая два небольших зазора величиной d, равна L. По обмотке сердечника, имеющей N витков, течет ток I. Определить величину поля B в зазоре. Рассеянием магнитного поля в зазорах пренебречь.

3. Длинный соленоид (длина L, радиус r, число витков N) подключается к источнику постоянной ЭДС . Через резистор с сопротивлением R (сопротивлением соленоида можно пренебречь). Найти электромагнитную энергию W, втекающую в соленоид за время установления тока.

Э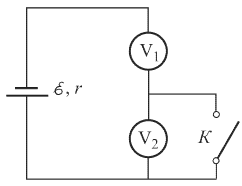 лектродинамика. Ток Вариант № 13

1. При замкнутом ключе K вольтметр V₁ показывает напряжение 0,8ε, где ε – ЭДС источника (см. рис.). Что покажут вольтметры V₁ и V₂ при разомкнутом ключе, если их сопротивления одинаковы?

2. Кольцо радиуса R с током I₁ лежит в одной плоскости с длинным прямым проводом, по которому течет ток I₂. Расстояние от центра кольца до провода a > R. Найти величину и направление силы, действующей на кольцо.

3. Обмотка электромагнита имеет сопротивление R = 10 Ом и индуктивность L = 0.2 Гн и находится под постоянным напряжением. В течение какого промежутка времени t в обмотке выделится количество теплоты, равное энергии магнитного поля в сердечнике?

Электродинамика. Ток Вариант № 14

1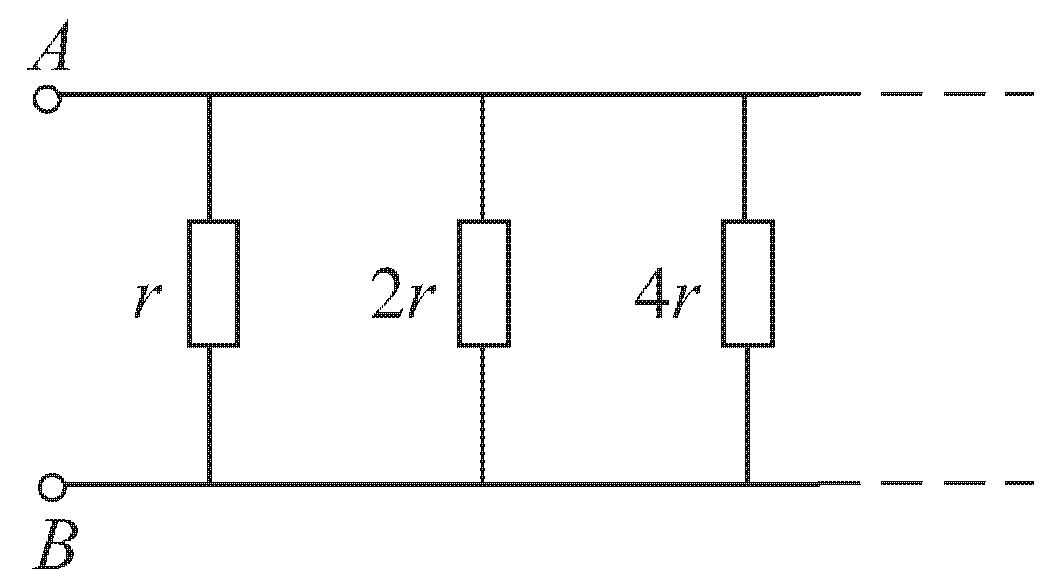 . Определите полное сопротивление R между точками A и B бесконечной цепи, параметры которой указаны на рисунке.

2. Сфера радиуса R, заряженная с поверхностной плотностью заряда , вращается вокруг своего диаметра с угловой скоростью . Найти величину и направление индукции магнитного поля в точках этого диаметра.

3. Проволочный каркас в виде квадрата с перекладиной, сделанной из той же проволоки, находится в однородном переменном магнитном поле, вследствие чего по проволокам идут индукционные токи. Магнитные поля индуцированных токов малы в сравнении с изменением магнитного поля. В каком случае и на какую долю индукционные токи выделяют большее количество теплоты: а) перекладина находится на середине квадрата? б) перекладина сдвинута к одной из сторон квадрата? в) перекладина делит площадь квадрата на части в отношении 1:3?

Электродинамика. Ток Вариант № 15

1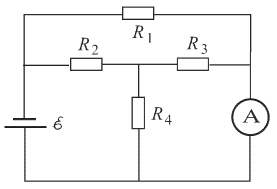 . Какой ток I_A течет через амперметр в схеме, показанной на рисунке 3 ЭДС источника ε = 7, 5 В, R₁ = 15 Ом, R₂ = R₃ = R₄ = 10 Ом.

2. Найти период малых колебаний квадратной рамки массой m с током I, относительно оси, проходящей через одну из ее сторон, если рамка находится в однородном магнитном поле с индукцией B, направленной перпендикулярно этой оси.

3. Цилиндрический электронный пучок радиусом R распространяется в свободном пространстве. Электроны летят с одинаковой скоростью 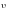, их концентрация равна n. Найдите величину и направление вектора Пойтинга внутри и вне пучка.

Электродинамика. Ток Вариант № 16

1. Присоединение к вольтметру некоторого добавочного сопротивления увеличивает предел измерения напряжения в n раз. Другое добавочное сопротивление увеличивает предел измерения в m раз. Во сколько раз к увеличится предельно измеримое вольтметром напряжение, если включить последовательно с вольтметром эти два сопротивления, соединенные между собой параллельно?

2. Заряженная частица движется в вязкой среде с постоянной скоростью во взаимно перпендикулярных электрическом и магнитном полях. Напряженность и индукция равны E и B. Найти скорость частицы и угол между скоростью и направлением B, если сила сопротивления пропорциональна скорости. Известно, что при движении только в одном электрическом поле скорость частицы равна v_o. Силу тяжести не учитывать.

3. Заряженный до напряжения U₀ и отключенный от источника плоский конденсатор с круглыми пластинами радиуса R пробивается электрической искрой вдоль своей оси. Считая разряд квазистационарным и пренебрегая краевыми эффектами, вычислите полный поток электромагнитной энергии, вытекающей из пространства между обкладками.

Э лектродинамика. Ток Вариант № 17

1. Какой ток I_A будет идти через амперметр в схеме, изображенной на рисунке? ЭДС источника равна ε. Рассмотрите два случая: а) R₁ = R₄ = R; R₂ = R₃ = 2R; б) R₁ = R₂ = R₃ = R; R₄ = 2R.

2 . На наклонной плоскости с углом наклона  лежит небольшая шайба, заряженная зарядом q. Масса шайбы m, коэффициент трения между шайбой и плоскостью ( < tg). Однородное магнитное поле с индукцией B направлено перпендикулярно плоскости (рис.). Шайбу отпускают. Найти установившуюся скорость шайбы.

3. К плоскому конденсатору, заполненным однородным диэлектриком с проницаемостями  = 10 и  =100, обкладки которого имеют форму дисков с зазором шириной d = 1 см, приложено переменное магнитное поле 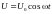с амплитудой 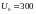В и круговой частотой  = 310⁶ с^-1. Найти амплитуды напряженности и индукции магнитного поля, как функции от расстояния до оси конденсатора.

Электродинамика. Ток Вариант № 18

1 . В схеме (см. рис.) вольтметр показывает напряжение U₁ = 20 В. Напряжение на входе цепи U_o = 100 В. Найдите отношение тока, идущего через вольтметр, к току, идущему через правую часть потенциометра, если отношение сопротивлений, на которые движок делит потенциометр n = 2/3, причем большее сопротивление имеет часть потенциометра, расположенная справа от движка.

2 . Электрон влетает в область однородного магнитного поля шириной l. Скорость электрона равна v и перпендикулярна границам области и вектору индукции B (рис.). Под каким углом к границе электрон вылетит из области?

3. Из материала с проводимостью  = 610⁷ (Омм^-1) изготовлен сплошной цилиндр длиной l = 4 см и радиусом R = 1 см. Цилиндр помещают в нестационарное магнитное поле, вектор индукции которого параллелен оси цилиндра. Величина магнитного поля изменяется по закону где r – расстояние до оси цилиндра, а R₁>R. Найти тепловую мощность, выделяющуюся в цилиндре за счет токов Фуко, если k = 10 Тл/с.

Э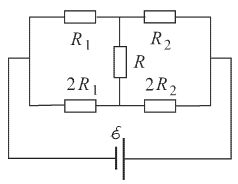 лектродинамика. Ток Вариант № 19

1. Найдите силу тока I₂, идущего через резистор с сопротивлением R₂ в схеме, параметры которой приведены на рис.

2 . Две параллельные проводящие рейки расположены в горизонтальной плоскости на расстоянии l = 1 м друг от друга. По ним без трения может двигаться проводящая перемычка массой m = 10 г. Рейки соединены друг с другом через конденсатор емкостью C = 100 мкФ (рис.). Система находится в вертикальном однородном магнитном поле с индукцией B = 10 Тл. На перемычку начинает действовать горизонтальная постоянная сила F = 0,04 Н, направленная параллельно рейкам. Определить заряд конденсатора через  = 1 с после начала движения перемычки.

3. Обкладки плоского конденсатора имеют форму дисков радиуса R. Пространство между обкладками заполнено однородным диэлектриком с диэлектрической и магнитной проницаемостями  и . Конденсатор включен в цепь переменного тока с силой . Считая разряд квазистационарным и пренебрегая краевыми эффектами, вычислить мгновенное значение плотности тока смещения j_см, считая ее независящей от r и магнитного поля H внутри конденсатора как функцию r, где r – расстояния от его оси.

Электродинамика. Ток Вариант № 20

1 . Цепь (см. рисунок) собрана из одинаковых резисторов и одинаковых вольтметров. Показания первого и третьего вольтметров U₁ = 10 B, U₃ = 8 В соответственно. Найдите показания U₂ второго вольтметра.

2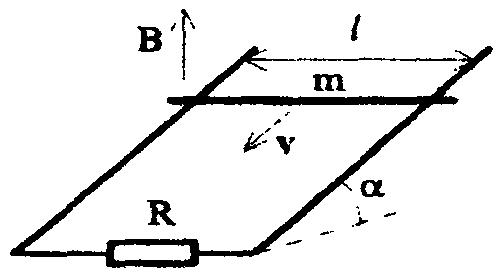 . Проводящие параллельные рельсы, наклоненные под углом  к горизонту соединены через сопротивление R (рис. 3). По ним без трения соскальзывает проводящая горизонтальная перемычка массой m. Расстояние между рельсами равно l. Определить установившуюся скорость движения перемычки, если вся система находится в однородном вертикальном магнитном поле с индукцией B. Сопротивлением всех остальных элементов кроме R пренебречь.

3. Плоский конденсатор, представляющий собой две круглые пластины радиуса R, расположенные на расстоянии d друг от друга, заряжают постоянным током I. Пространство между обкладками заполнено однородным диэлектриком с диэлектрической и магнитной проницаемостями  и . Определить напряженность магнитного поля H, возникающего в зазоре между пластинами, как функцию расстояния до оси конденсатора r и энергию магнитного поля, заключенную в конденсаторе. Плотность тока смещения считать постоянной.

Электродинамика. Ток Вариант № 21

1. Пластины плоского конденсатора имеют форму квадратов со стороной a = 21 см. Расстояние между пластинами составляет d = 2 мм. Конденсатор присоединен к полюсам источника постоянного напряжения U = 750 В. В пространство между пластинами с постоянной скоростью v = 8 см/с вдвигают стеклянную пластинку толщины d = 2 мм. Какой силы ток I пойдет при этом по цепи? Диэлектрическая проницаемость стекла  = 7.

2 . Найти ЭДС индукции, возникающую в бесконечном прямом проводе, если в контуре в виде прямоугольного треугольника течет ток I. Вершина прямого угла лежит на проводе, а гипотенуза параллельна проводу.

3. Медное кольцо радиусом r соединено проводящими спицами с центром. К центру и кольцу подключен резистор сопротивлением R. На кольцо намотана нить с грузом массой m. Кольцо вращается без трения вокруг оси, проходящей через его центр и находится в однородном магнитном поле с индукцией B, направленной параллельно его оси (рис.). Найти установившуюся скорость опускания груза.