2 курс ИТиП лаб 6

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Электроники"

ОТЧЕТ

по дисциплине "Информационные технологии и программирование"

на тему:

"Решение оптимизационных задач численными методами. Вариант 7."

Выполнил

Проверил

Кандидат технических наук, доцент ______________ Т. П. Косичкина

Москва 2023

Цель работы: Изучить самостоятельно по указанной литературе основные понятия теории оптимизации: постановка задачи, условия сходимости, оценка погрешности. Изучить численные методы решения одномерных и многомерных задач оптимизации

Выполнение

Задание 1. Разработайте программы (на языке С++) для нахождения точки минимума (максимума) функции с заданной точностью методами дихотомии и золотого сечения. В основной программе main() производится консольный ввод точности вычисления и вызов функции, выполняющей алгоритм нахождения минимума функции. Каждая из функций должна возвращать число итераций, при которых была достигнута заданная точность. Выбор той или иной функции, а также возможность повторного выполнения программы должен производится в соответствии с меню.

Таблица 1 – 7 Вариант функции для решения задач одномерной оптимизации.

Номер варианта	Целевая функция	Точность
7.	F(x)=x*sin(x+1)-cos(x-5)

Рисунок 1 - График функции варианта 7.

Ниже на рисунке 2 представлена часть программы, где для нахождения точки минимума функции с заданной точностью используется метод дихотомии.

Рисунок 2- Метод дихотомии.

На рисунке 3 представлен метод золотого сечения для нахождения точки минимума.

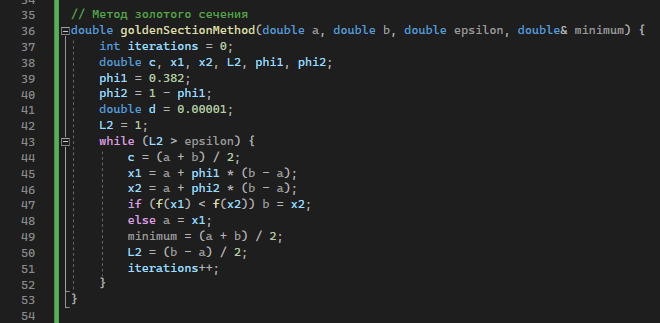
Рисунок 3 - Метод золотого сечения.

В соответствии с заданием создадим меню для выбора необходимой функции.

Рисунок 4 - Меню для выбора необходимой функции.

Рисунок 5 – Результат работы программы.

Задание 2. Написать программу для решения задачи многомерной оптимизации численным методом. Для нахождения координат минимума функции заданным методом с точностью 10-4 напишите на языке С++ функцию, прототип которой задайте самостоятельно. Функция должна предусматривать вывод числа итераций, за которые достигается требуемая 2 точность. Включите данную функцию в меню предыдущего задания. Получите результат и сравните его с результатом, полученным аналитически, сделайте выводы.

Рисунок 6 – Функция 7-го варианта.

Рисунок 7 – Листинг программы.

Рисунок 8 – Результат работы программы.

Вывод: Цель работы была успешно достигнута. Изучение основных понятий теории оптимизации, таких как постановка задачи, условия сходимости и оценка погрешности, позволило углубить знания в этой области. Также были изучены численные методы решения одномерных и многомерных задач оптимизации, что дало возможность практически применить полученные знания. В результате работы были приобретены навыки самостоятельного изучения и применения теории оптимизации, что будет полезно для дальнейшей профессиональной деятельности.