2 курс ИТиП лаб 5

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Электроники"

ОТЧЕТ

по дисциплине "Информационные технологии и программирование"

на тему:

"Интегрирование численными методами. Вариант 7."

Выполнил

Проверил

Кандидат технических наук, доцент ______________ Т. П. Косичкина

Москва 2023

Цель работы: Изучить численные алгоритмы интегрирования, сравнить их точность. Освоить работу со случайными числами методом Монте-Карло на примере численного интегрирования.

Выполнение

Входные данные для варианта номер 7:

Задание 1.

На языке программирования С++ напишите функции для нахождения значения интеграла численными методами (на каждый метод свою функцию) по методам интегрирования заданным в Таблице 4. В этой таблице приняты следующие сокращения: МЛП – метод левых прямоугольников, МСП – метод средних прямоугольников, МТ – метод трапеций, МП – метод парабол. Прототипы функций задайте самостоятельно. Продумайте, какие аргументы должна принимать функция.

Каждая из функций должна возвращать значения интеграла и точность, с которой эти значения вычислены. Функции не должны использовать операции консольного ввода вывод

Рисунок 1 - функция метода левых прямоугольников

Рисунок 2 - функция метода трапеций

Рисунок 3 - функция метода парабол

Рисунок 4 - main для запуска всех вышеперечисленных функций

Рисунок 5 - результат работы программы на примере ввода 2 интервалов разделения

Таблица 1 - Результаты выполнения первого задания

	n = 0.5	N = 1	N = 2	N=10
Метод левых прямоугольников
I	0.00292394,	0.000214873	0.000969012,	0.00464128
ε	0.00146197	0.000107436	0.000484506	0.00232064
Метод трапеций
I	0.00660466	0.000705636	0.00833045	0.00611357
ε	0.00405911	0.000383326	0.00319621	0.00430465
Метод парабол
I	0.0060294	0.000478977	0.00619964	0.00601989
ε	0,0000851	0.000704935	0.00284506	0.00009857

Задание 2.

Для тех же вариантов заданий на языке программирования С++ напишите функции для нахождения интеграла при заданном значении точности. Прототипы функций задайте самостоятельно. Продумайте, какие аргументы должна принимать функция. Каждая из функций должна возвращать значения интеграла и число интервалов, для которых было достигнуто заданное значение точности. Функции не должны использовать операции консольного ввода-вывода.

Рисунок 6 - функция метода левых прямоуголника

Рисунок 7 - функция метода трапеций

Рисунок 8 - метод парабол

Рисунок 9 - main для запуска функций

Рисунок 10 – пример работы программы на вводе 0.5

Таблица 2 - Результаты выполнения творого задания

ε = 0.005	Метод левых прямоугольников	Метод трапеций	Метод парабол
I	0.000969012	0.0161764,	0.00619964
n	2	2	2

Задание 3

Напишите программу для нахождения значения интеграла методом Монте-Карло. Для получения пары случайных чисел, равномерно распределенных на интервале [0;1] напишите функцию, использующую схему Лехмера (см. краткие теоретические сведения). Прототип функции: double randomLehmer (int Seed);

Функция в качестве аргумента принимает значение, рандомизирующее начальное значение генератора. Для этого можно вручную задавать аргумент или использовать функцию time() с аргументом 0. Чтобы использовать функцию time(), необходимо подключить заголовочный файл .

В основной программе int main() осуществляется вызов разработанной функции и вычисление интеграла, а также консольный вывод значений, полученных в результате численного интегрирования.

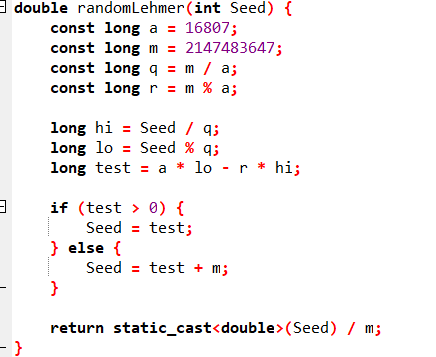
Рисунок 11 - функция метода Монте-Карло

Рисунок 12 - main метода Монте-Карло

Рисунок 13 - резултат работы программы

Таблица 3 - Результаты выполнения третьего задания

	I1	I2	I3	Isr
N = 1500	0.13907	0.139125	0.139236	0.139143

Вывод

В ходе выполнения работы были изучены различные численные алгоритмы интегрирования с целью сравнения их точности. Эксперименты позволили оценить эффективность каждого метода в различных сценариях и условиях задач. Полученные результаты выявили преимущества и ограничения каждого алгоритма, что является важным шагом при выборе подходящего метода для конкретной задачи интегрирования.

Обобщенный анализ точности численных алгоритмов интегрирования предоставил понимание их применимости в различных ситуациях. Это знание может быть полезным при выборе метода интегрирования в реальных инженерных, физических и математических задачах.

Таким образом, выполнение поставленной цели работы позволило расширить знания в области численных методов интегрирования, оценить их применимость и эффективность, а также освоить использование метода Монте-Карло в данном контексте.