2 курс ИТиП лаб 4

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Электроники"

ОТЧЕТ

по дисциплине "Информационные технологии и программирование"

на тему:

"Решение нелинейных уравнений численными методами. Вариант 7."

Выполнил

Проверил

Кандидат технических наук, доцент ______________ Т. П. Косичкина

Москва 2023

Цель работы: Изучить численные алгоритмы нахождения корней нелинейных уравнений, для чего по указанной литературе изучить: постановку задачи численного решения нелинейных уравнений; аналитический и графический методы отделения корней; условия окончания вычислений; вопросы сходимости и оценки погрешности методов. Овладеть принципами создания циклических алгоритмов на языке С++ с применением инструкций цикла.

Выполнение

Входные данные для 7 варианта:

Функция: tg(x/2)-ctg(x/2)+x=0;

Интервал [1;2];

Число итераций N = 12;

Точность ε - 10^-4

Задание 1.

Выберите для выполнения лабораторной работы свой вариант. Для выбранного варианта разработайте подпрограммы (на языке С++) нахождения корня нелинейного уравнения на заданном интервале тремя методами (методом деления отрезка пополам, методом Ньютона и методом простой итерации), каждый для двух вариантов цикла: регулярного (число итераций N задано в таблице) и итерационного (точность ε задана в таблице). Основная программа main() работает следующим образом: сначала делается запрос на ввод начального приближения (это может быть α, β или x0) к тому корню, который надо получить; после того как введены требуемые данные, идет обращение к подпрограмме, выполняющей вычисления, а затем вывод результатов. Различные методы нахождения корня уравнения необходимо оформить в виде отдельных подпрограмм, всего должно быть шесть подпрограмм (функций). Прототипы функций задать самостоятельно. Организовать меню с возможностью выбора метода нахождения корней и вариантов цикла. Для итерационного цикла выполнять вычисления пока не будет достигнута точность, заданная в таблице 1. Предусмотреть вывод числа итераций на экран и сравнить их для разных методов нахождения корней уравнения. Для регулярного цикла, для заданного в таблице 1 числа итераций N, сравнить точность полученных результатов для разных методов нахождения корней уравнения

Рисунок 1 - функция

Рисунок 2 - регулярный метод деления отрезка пополам

Рисунок 3 - итерационный метод деления отрезка пополам

Рисунок 4 - регулярный метод ньютона

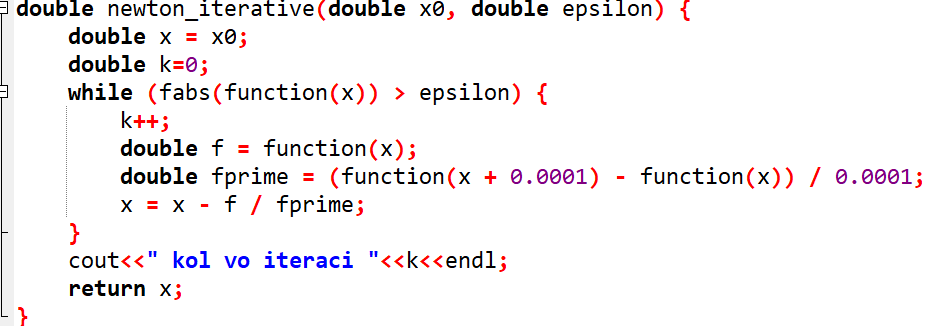
Рисунок 5 - итеративный метод Ньютона

Рисунок 6 - регулярный метод простой итерации

Рисунок 7 - итерационный метод простой итерации

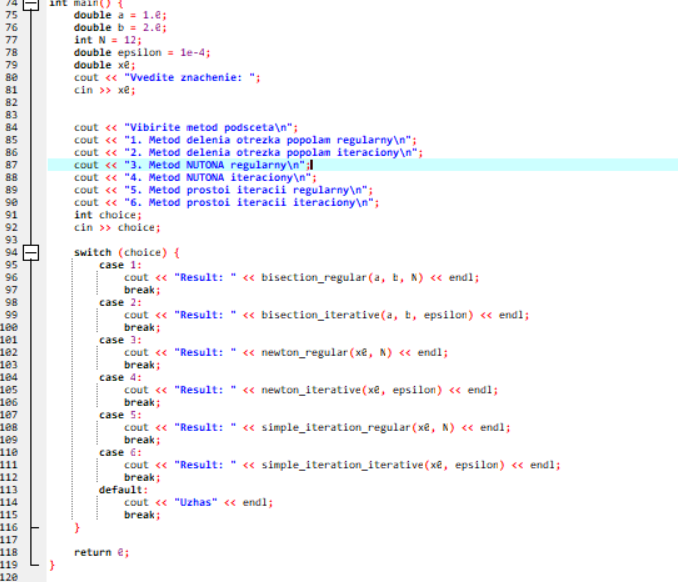
Рисунок 8 - пример цикла main с возможностью выбора метода нахождения корня уравнения

Таблица 1- Результаты выполнения заданий на примере числа (2).

	Точность ε при N=12	Число итераций N при ε = 10^-4
Метод деления отрезка пополам	0.002446	14
Метод Ньютона	0.001007	3
Метод простой итерации	0,00877	243

Задание 2.

Нарисовать график функции, а также график сходимости к указанному корню для первых пяти итераций, для чего предусмотреть в процедуре нахождения корня.

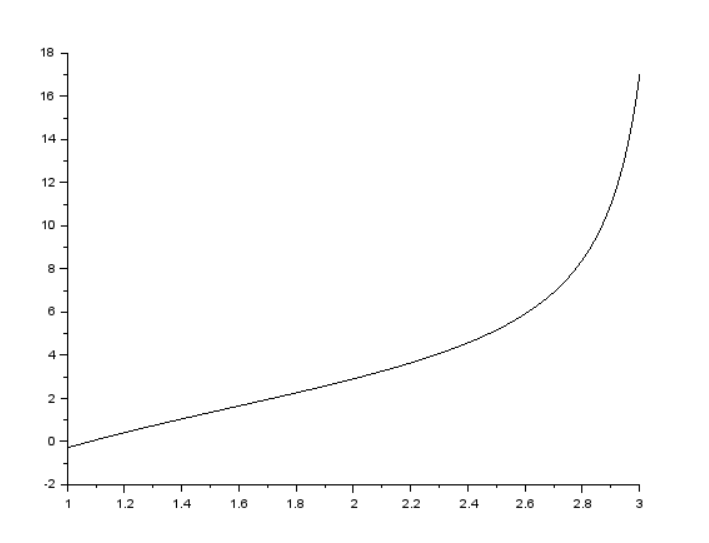
Рисунок 9 - график который наглядно показывает как выглядит функция tg(x/2)-ctg(x/2)+x=0

Вывод

В результате работы были написаны функции для каждого из этих методов, как с использованием фиксированного числа итераций, так и с использованием заданной точности. Кроме того, были проведены вычислительные эксперименты для каждого метода с различными начальными приближениями и заданными параметрами. Таким образом, цель работы была успешно достигнута, и были получены навыки применения численных алгоритмов нахождения корней нелинейных уравнений с использованием языка C++.