1.3. Дублеты щелочных металлов и спин электрона

Линии главных серий щелочных металлов являются дублетными. Хорошо известен пример D-линии натрия, дублетную природу которой обнаруживают даже простейшие спектроскопические приборы. Расщепление линии довольно значительно - оно составляет 6Å; две компоненты ее обозначаются как D₁ и D₂, и длины волн их равны исоответственно.Анализ термов в спектрах щелочных металлов, к которым принадлежит и спектр натрия, совершенно определенно показывает, что в этих спектрах

термы синглетны,

термы дублетны.

Этот экспериментальный факт невозможно объяснить ни с точки зрения теории Бора, ни с точки зрения изложенной до сих пор волновой механики. Рассмотрение движениея электрона в атоме, исходя из его трех степеней свободы приводит к заключению, что движение полностью определяется и описывается тремя квантовыми числами . Любое дальнейшее расщепление термов, помимо обусловленного этими квантовыми числами, необъяснимо до тех пор, пока мы придерживаемся представления, что движение электрона не более чем троекратно периодично.

Учитывая полученные к 1925 г. экспериментальные данные, Уленбек и Гаудсмит выдвинули гипотезу о том, что если бы можно было рассматривать электрон как тело конечной протяженности, то, подобно всякому протяженному телу, он обладал бы, помимо трех поступательных, тремя вращательными степенями свободы. Соответственно он имел бы механический момент и, кроме того, как всякое вращающееся заряженное тело, магнитный момент. Авторы гипотезы предположили, что экспериментальные факты можно понять, приписав электрону механический момент и магнитный момент столь же формальным образом, как приписываются ему масса и заряд. Что же касается величин магнитного и механического моментов, то в первую очередь необходимо измерить их в экспериментах, а впоследствии попытаться вывести эти значения теоретически.

Свойство электрона, вследствие которого он обладает механическим и магнитным моментами, называется его спином. Величина механического момента следует непосредственно из фактов, известных о спектрах щелочных металлов.

Подобно всякому моменту, момент электрона должен, конечно, быть квантованным, причем то же самое справедливо для его компоненты в выделенном направлении (внешнее магнитное поле). Поэтому, если величина механического спинового момента равна (в единицах), то по правилам пространственного квантования для него должны быть возможны ориентации (или наклонов) относительно выделенного направления, в которых значения выбранной компоненты, обозначаемые через, отличаются друг от друга на единицу.

Аналогичные соотношения имеют место в атоме Бора, где плоскость орбиты, отвечающей моменту , имеет в точностивозможных ориентации относительно выделенного направления. Эти ориентации характеризуются компонентамимомента в выбранном направлении. Такая экстраполяция представлений об орбитальном моменте на спиновый момент не только оправдывается тем, что выведенные из нее следствия полностью согласуются с опытом, но и может быть обоснована теоретически.

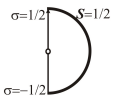
Рис.6. Ориентация спина по отношению к выделенному направлению

Таким образом, спин электрона должен иметьвозможных ориентации относительно выбранного направления. Но опыт показывает, что, за исключениемтермов, все термы натрия дублетны. Этот факт позволяет сделать вывод о том, что спин имеет только две возможные ориентации (Рис.6). Но это только в том случае если верно предположение, что спин определяет расщепление термов. Следовательно, должно быть, или (в единицах ). Две возможные ориентации характеризуются компонентами

На первый взгляд, появление полуцелых «квантовых чисел» противоречит представлениям о квантовании момента. Однако необходимо отметить, что представление о вращающемся протяженном электроне имеет лишь эвристическое значение, и строго говоряневерна. Если например рассмотреть точку на поверхности электрона, то она должна двигаться со сверхсветовой скоростью, чтобы вычисленные по классической теории значения механического и магнитного момента согласовались с экспериментально найденными значениями. Использование полуцелых компонент для спина приводит к результатам, находящимся в полном согласии с экспериментальными данными. С другой стороны, волновая механика обладающего спином электрона в форме, которую ей придал Дирак, приводит к полуцелым значениям спина автоматически вследствие только условий линейности и релятивистской инвариантности без каких-либо дополнительных предположений.

Вращающийся вокруг ядра электрон обладает орбитальным моментом и спиновым моментом. Возникает вопрос о правиле сложения этих двух моментов. Теория Бора ответила бы, что это должно происходить по правилам сложения векторов. То же самое правило сложения дает волновая механика, хотя доказательство этого (Вигнер,Нейман, 1927 г.) требует современных математических методов (теории групп). Таким образом, искладываются векторно, образуя результирующий (или полный) момент(в единицах), так что. Следуя Зоммерфельду, иногда называют«внутренним квантовым числом» которое представляет полный механический момент атома. Допустимые значения должны отличаться на целые числа. Так как, то единственными возможностями будут следовательно, в этом случае значениеполуцелое. Каждомузначению соответствуют два возможных значения полного механического момента, так что соответствующие термы оказываются дублетами. Одни лишь термысоставляют исключение. Они всегда синглетны, поскольку в этом случае допустимо только значение , ибо полный моментвсегдадолжен быть положительным. Двойная возможность ориентации спина электрона относительно его орбиты эквивалентна расщеплению уровней энергии вследствие магнитного взаимодействия спина и орбиты. Величина расщепления прямо равна энергии, необходимой для разворота спина в магнитном поле орбиты из одной орентации относительно в другую.

Рассмотрим в качестве примера линию натрия. Анализ термов показывает, что верхнее состояние представляет собойтерм, а нижнеетерм. Первый из них - дублет, соответственно двум возможным значениям полного момента: и нижний, как и полагаетсяs-терму, является синглетом . Линия соответствуетпереходу с терма (внутреннее квантовое число, линия - переходу с терма для которого с.

Правило векторного сложения можно применять и к случаю нескольких электронов; в этом случае орбитальные моменты отдельных электронов и их спиныскладываются, образуя полный момент. Здесьбудет целым илиполуцелым, в зависимости от того четно или нечетно число электронов. Аналогично и проекция полного момента в выбранном направлении может быть целой или полуцелой.

В заключение упомянем еще тот факт, что по самому смыслу как полного момента система как целое вращается с постоянной угловой скоростью вокруг направления. Это приводит к правилам отборадля испускаемого излучения. Однако теория указывает в полном согласии с опытом, что имеются еще и переходы с. Они соответствуют такому изменению состояния, при котором полный момент не меняется. Что такие переходы разрешены, тогда как переходы сзапрещены, можно объяснить, опираясь на принцип соответствия.