Билет №18-19. Определение локальных экстремумов функции одной переменной. Достаточные условия локального экстремума.

Функция f(x) имеет локальный максимум в точке x_0, если в некоторой окрестности точки x₀, выполняется неравенство .

Функция f(x) имеет локальный минимум в точке x₀, если в некоторой окрестности точки x₀, выполняется неравенство .

Точки локального максимума и локального минимума называют точками локального экстремума.

Слово "локальный" для краткости опускают и говорят максимум и минимум функции.

Функция может достигать экстремума только в тех точках области определения, в которых производная равна нулю или не существует. Такие точки называются критическими.

Замечание. Критическая точка не обязательно является точкой экстремума.

Если функция f(x) определена в некоторой окрестности точки x₀ и её производная при переходе через точку x₀ меняет знак, то точка x₀ является точкой экстремума функции.

Функция может достигать экстремума только в тех точках области определения, в которых производная равна нулю или не существует. Такие точки называются критическими.

Замечание. Критическая точка не обязательно является точкой экстремума.

Если функция f(x) определена в некоторой окрестности точки x₀ и её производная при переходе через точку x₀ меняет знак, то точка x₀ является точкой экстремума функции.

Билет №20. Определение и признаки выпуклости функции, точки перегиба графика функции

Пусть функция f(x) дифференцируема в любой точке промежутка (a;b), тогда существует касательная к графику функции y=f(x), проходящая через любую точку М(x, f(x)) этого графика (a<x<b), причем эта касательная не параллельна оси OY.

выпуклый вверх выпуклый вниз

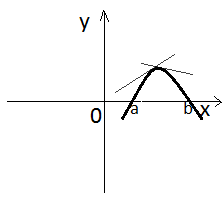График функции y=f(x) является выпуклым вверх (выпуклым) в промежутке (a;b), если в пределах данного промежутка он лежит не выше любой своей касательной.

График функции y=f(x) является выпуклым вниз (вогнутым) в промежутке (b;c), если в пределах данного промежутка он лежит не ниже любой своей касательной.

Точка графика функции, отделяющая части графика, выпуклые в разных направлениях, называется точкой перегиба графика функции

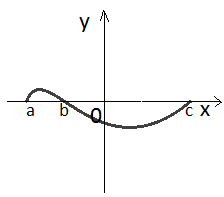(b-точка перегиба)

В точке перегиба касательная пересекает график функции.

• Если во всех точках промежутка (a;b) вторая производная функции f(x) отрицательна (f , то график функции y=f(x) является выпуклым вверх ( выпуклым) в промежутке (a;b).

• Если во всех точках промежутка (b;c) вторая производная функции f(x) положительна ( , то график функции y=f(x) является выпуклым вниз ( вогнутым) в промежутке (b;с).

Для нахождения точек перегиба непрерывной функции нужно:

1. Найти область определения функции.

2. Найти первую производную функции.

3. Найти вторую производную функции.

4. Приравнять вторую производную к нулю, определить её корни.

5. В области определения функции найти точки, в которых вторая производная не существует.

6. Исследовать найденные точки на перегиб, установив знак второй производной слева и справа от этих точек. Если смена знака второй производной происходит, то в данной точке функция имеет перегиб. В противном случае, перегиба нет.

Пример. Определить направление выпуклости и точки перегиба графика функции Решение:

1. Функция определена на промежутке .

2. Найдем первую производную функции

.

3. Найдем вторую производную функции

.

4. Приравняем вторую производную к нулю и найдем корни:

2 .

5. Производная определена на промежутке .

6. При переходе через точку , производная знака не меняет, следовательно, точка x₁ не является точкой перегиба.

При переходе через точку , производная меняет знак, следовательно, точка x₂ является точкой перегиба.

Так как f(x) непрерывна, то на промежутке ее график является выпуклым вверх, а на промежутке выпуклым вниз.

Ответ: точка перегиба, график выпуклый вверх, график выпуклый вниз.