Оглавление

БИЛЕТ №1 Матрицы и их классификации 1

БИЛЕТ №2 Матрицы и действия над ними. 4

Билет №4. Системы линейных уравнений: основные понятия, формы записи. Основная и расширенная матрица системы линейны уравнений. 6

Билет №5. Теорема Кронекера-Капелли. Исследование системы линейных уравнений. 8

Билет №6 (Метод Гаусса решения систем линейных уравнений) 8

Билет № 7 (Числовые множества) 9

Билет №8. Понятие функции 11

Билет№9.Предел функции. Предел функции в бесконечности 12

Билет№10. Основные теоремы о пределах: 14

Билет №11. Непрерывность функции в точке. Непрерывность функции на промежутке. Точки разрыва функции. 15

Билет №12. Производная функции. Теорема о связи дифференцируемости и непрерывности функции. Геометрический, физический, экономический смысл производной. 16

Билет 15. Таблица производных основных элементарных функций. 19

Билет 16. Производные и дифференциалы высших порядков 19

Билет № 17. Монотонность, экстремумы и выпуклость. Функции одной переменной. 21

Билет №18-19. Определение локальных экстремумов функции одной переменной. Достаточные условия локального экстремума. 24

Билет №20. Определение и признаки выпуклости функции, точки перегиба графика функции 25

Билет №21. Асимптоты графика функции. 27

Билет №23 (Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла) 29

Билет №24 (Таблица неопределенных интегралов) 32

Билет №25. Основные методы интегрирования. Табличное интегрирование. 32

Билет №26. Замена переменной в неопределенном интеграле. 34

Билет №27. Интегрирование по частям 36

Билет №28. Определенный интеграл. Площадь криволинейной трапеции. 37

Билет № 29: Свойства определенного интеграла 38

Билет №30: Формула Ньютона-Лейбница 40

Билет №31. Формулы замены переменной и интегрирование по частям в определенном интеграле 42

Билет №32. Вычисление площади с помощью определенного интеграла 43

Билет №1 Матрицы и их классификации

Система 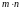элементов, расположенных в виде прямоугольной таблицы из строк и столбцов, называется матрицей размерности и записывается в виде:

Матрицы обозначаются заглавными буквами латинского алфавита, а набор элементов матрицы помещается в круглые скобки.

Элемент матрицы, расположенный на пересечении i-ой строки и j-го столбца, называется i,j-м элементом и записывается  a_i j 

i – номер строки в которой расположен элемент,

j – номер столбца в котором расположен элемент

Матрицы позволяют оперировать с массивами чисел, функций.

Матрица размерности называется квадратной матрицей порядка .

Матрица, состоящая из элементов одной строки, размерности 1×n, называется матрицей-строкой

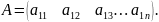
Матрица, состоящая из элементов одного столбца, размерности m×1, называется матрицей-столбцом.

.

Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. a_ij = 0, ∀ i, j.

Д иагональ квадратной матрицы, идущая от левого верхнего угла к правому нижнему, называется главной диагональю.

Диагональ идущая от левого нижнего к правому верхнему углу, называется побочной.

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

   , 

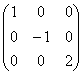Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы нули, называется единичной матрицей и обозначается:

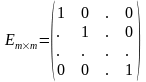
Единичная матрица является диагональной.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

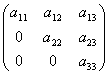Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах.

Пример.

Матрица, полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A^T:

, 

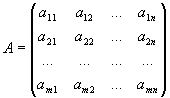Верно соотношение: (A^T )^T =A;

Билет №2 Матрицы и действия над ними.

1. Складывать можно только матрицы одинаковых размеров

(А m n – матрица размера m n)

Если А m n = (a ij ) , B m n= (b ij) , то их сумма равна матрице C m n=(C ij)

где C ij= a ij + b ij ,C=A+B

Суммой матрицы A и B с одинаковыми размерами называется матрица, элементы которой будут равны сумме соответствующих элементов матрицы A и B.

S=A+B S_ij=a_ij+b_ij Пример:

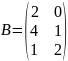
2. Аналогично выполняется разность матриц, тогда C ij= a ij - b ij , т.е. C=A-B

Разностью матриц А и В с одинаковыми размерами называется матрица, элементы которой будут равны разности соответствующих элементов матриц А и В.

R=A-B r_ij=a_ij-b_ij

3. Произведение матрицы А m n = (a ij ) на число k,где k ≠ 0, равно B m n , b ij = k a ij , т.е. B = k A

Произведением матрицы А на скаляр (число) 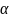называется матрицей, элементы которой получаются из элементов матрицы А, умноженных на .

Матрица -А называется противоположной матрице А.

Произведение матрицы А размерностью m*n на матрицу B размерность n*q называется матрица с размером m*q, каждый элемент которой вычисляется по формуле:

C_iq=a_i1*b_iq+a_i2*b_2q+…+a_in*b_mq

2 матрицы можно перемножить, если количество строк второй матрицы равно количество столбцов 1ой матрицы.

A_m*n*B_n*q=C_m*q

Матрица произведения содержит столько строк, сколько 1ый сомножитель и столько столбцов, сколько второй сомножитель, а элемент C_iq равен сумме парных произведений элементов i-строки и q-столбца.

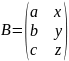
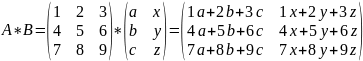
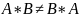Произведение матриц на обладает переместительным законом.

Элементарными преобразованиями над строками матриц называются следующие преобразования строк:

1. умножение строки на ненулевое число;

2. перестановка двух строк;

3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число;

4. удаление из матрицы или приписывание к матрице ряда, целиком состоящего из нулей;

5. Транспонирование матрицы, т.е. элементы каждой строки заданной матрицы А , заменяют столбцом с тем же номером, получают матрицу А^Т

Если от матрицы A к матрице B можно перейти с помощью элементарных преобразований над строками, то такие матрицы называют эквивалентными и обозначают A~B.

Свойства:

1. А+В=В+А

2. 

3. (

4. (А+В)+С=А+(В+С)

5. (

6.