Правила выбора коэффициента взаимосвязи.
Величина коэффициента взаимосвязи рассчитывается с учетом шкалы, использованной для измерений.
Для оценки взаимосвязи, когда измерения производят в шкале отношений или интервалов и форма взаимосвязи линейная, используется коэффициент корреляции Бравэ-Пирсона (коэффициенты корреляции для других шкал измерения в данном пособии не рассматриваются). Обозначается он латинской буквой – r. Вычисление значения r чаще всего производят по формуле:
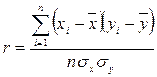, где x
и y
– средние арифметические значения
показателей x и y, и – средние квадратические
отклонения, n – число измерений
(испытуемых).
В некоторых случаях тесноту взаимосвязи определяют на основании коэффициента детерминации D, который вычисляется по формуле:
.
Этот коэффициент определяет часть общей вариации одного показателя, которая объясняется вариацией другого показателя. Например, коэффициент корреляции r = –0,677 (между результатами в беге на 30 м с ходу и тройном прыжке с места). Коэффициент детерминации равен:
.
Следовательно, 45,8 % рассеяния спортивного результата в тройном прыжке объясняется изменением результатов в беге на 30 м. Иными словами, на оба исследуемых признака действуют общие факторы, вызывающие варьирование этих признаков, и доля общих факторов составляет 45,8%. Остальные 100% – 45,8% = 54,2% приходятся на долю факторов, действующих на исследуемые признаки избирательно.
Систематические и случайные ошибки измерений. Способы устранения систематической погрешности.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей.
Это может быть достигнуто следующими путями:
- устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;
- определением поправок и внесением их в результат измерения;
- оценкой границ неисключенных систематических погрешностей.
Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности.