
иксис5
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИС
отчет
по лабораторной работе №5
по дисциплине «Инфокоммуникационные системы и сети»
Тема: Формулы Эрланга
Вариант 169
Студентка гр. |
|
|
Преподаватель |
|
Колбанев М.О. |
Санкт-Петербург
2023
Листинг программного кода
import matplotlib.pyplot as plt
import numpy as np
#первая формула
def erlang1(intensity, devCount):
if devCount <= 0:
return 1
temp = intensity * erlang1(intensity, devCount - 1)
return temp / (devCount + temp)
#вторая формула
def erlang2(intensity, devCount):
temp = erlang1(intensity, devCount)
return temp / (1 - ((intensity / devCount) * (1 - temp)))
def erlang2_queue(intensity, devCount):
temp1 = intensity * erlang1(intensity, devCount)
temp2 = devCount - intensity
return temp1 / (temp2 + temp1) * devCount / temp2
n = 169
# 1 часть
x = np.linspace(0, 30000, 100)
plt.plot(x, [erlang1(i, 2 * n) for i in x])
plt.xlabel("Интенсивность поступающей нагрузки")
plt.ylabel("Вероятность блокировки заявок")
plt.grid()
plt.show()
x = np.linspace(1, 140, 100)
plt.plot(x, [erlang2(n, i) for i in x])
plt.xlabel("Интенсивность поступающей нагрузки")
plt.ylabel("Вероятность блокировки заявок")
plt.grid()
plt.show()
# 2 часть
x = np.linspace(150, 2 * n, 100)
plt.plot(x, [erlang2(i, 2 * n) for i in x])
plt.xlabel("Число обслуживающих устройств")
plt.ylabel("Вероятность ожидания начала обслуживания")
plt.grid()
plt.show()
x = np.linspace(150, 2 * n - 1, 100)
plt.plot(x, [erlang2_queue(i, 2 * n) for i in x])
plt.xlabel("Интенсивность поступающей нагрузки")
plt.ylabel("Средняя длина очереди")
plt.grid()
plt.show()
x = np.linspace(n, 140, 100)
plt.plot(x, [erlang2(n, i) for i in x])
plt.xlabel("Число обслуживающих устройств")
plt.ylabel("Вероятность ожидания начала обслуживания")
plt.grid()
plt.show()
x = np.linspace(n + 1, 140, 100)
plt.plot(x, [erlang2_queue(n, i) for i in x])
plt.xlabel("Число обслуживающих устройств")
plt.ylabel("Средняя длина очереди")
plt.grid()
plt.show()
1 часть
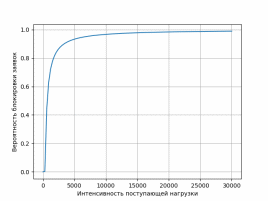
Рисунок 1.1. График зависимости вероятности блокировки заявок от
интенсивности поступающей нагрузки при числе обслуживающих устройств 2*n
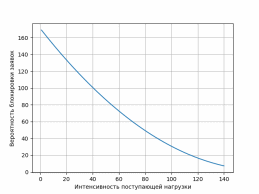
Рисунок 1.2. График зависимости вероятности блокировки заявок от числа
обслуживающих устройств при интенсивности поступающей нагрузки n
2 часть
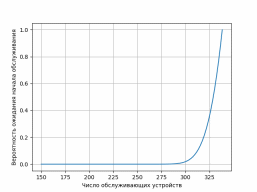
Рисунок 2.1. График зависимости вероятности ожидания начала обслуживания от интенсивности поступающей нагрузки при числе обслуживающих устройств 2*n
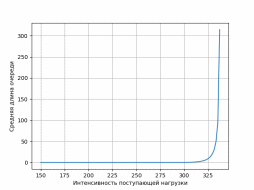
Рисунок 2.2. График зависимости средней длины очереди от интенсивности поступающей нагрузки при числе обслуживающих устройств 2*n
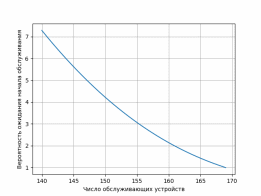
Рисунок 2.3. График зависимости вероятности ожидания начала обслуживания от интенсивности поступающей нагрузки при числе обслуживающих устройств n
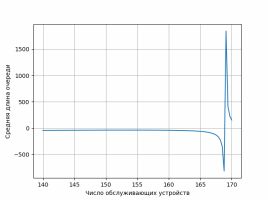
Рисунок 2.4. График зависимости средней длины очереди от интенсивности поступающей нагрузки при числе обслуживающих устройств n
Вывод: в ходе работы были изучение и реализованы на языке Python первая и вторая формулы Эрланга. В самом коде были написаны рекуррентные функции для расчёта, а также построены графики зависимостей, которые показывают поведение системы в различных условиях.
