иксис2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИС

отчет

по лабораторной работе №2

по дисциплине «Инфокоммуникационные системы и сети»

Тема: Потоки заявок и освобождений. Время обслуживания.

Вариант 169

Студентка гр.
Преподаватель		Колбанев М.О.

Санкт-Петербург

2023

Часть 1.

1. Временная диаграмма СМО G/G/3

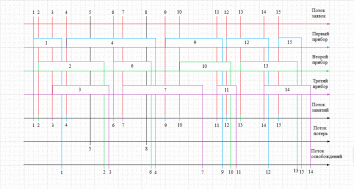
2. Рассчитать среднее время (1 клетка = 1 минута):

• Интервалов времени между поступившими заявками: (1+3+3+5+5+2+5+4+3+8+2+3+5+3)/14 = 3,71 минут

• Занятости всех приборов: (6+19+12+9+5+14+8+11+12+12+17+4+10)/13 = 10,69 минут

• Занятости 1-ого прибора: (6+19+12+9+5)/5 = 10,2 минуты

• Между моментами занятий: (1+3+3+10+2+9+3+8+2+3+5+3)/12 = 4,33 минуты

• Между моментами потерь: 12/1 = 12 минут

• Между моментами освобождений: (9+1+9+1+10+4+2+1+7+6+1+2)/12 = 4,42 минуты

3. Временная диаграмма СМО G/G/3 (потеряно 10 заявок)

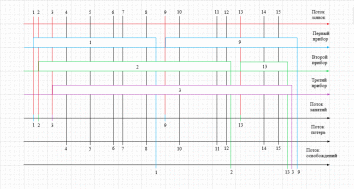
4. Временная диаграмма СМО G/G/3/2

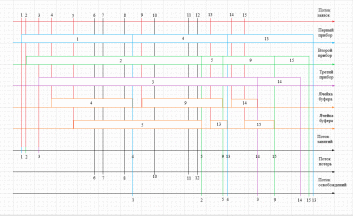
5. Рассчитать среднее время для диаграммы 2(1 клетка = 1 минута):

• Интервалов времени между поступившими заявками: (1+3+3+5+5+2+5+4+3+8+2+3+5+3)/14 = 3,71 минут

• Занятости всех приборов: (26+41+51+28+10)/5 = 31,2 минуты

• Занятости 1-ого прибора: (26+28)/2 = 27 минут

• Между моментами занятий: (1+3+24+16)/4 = 11 минут

• Между моментами потерь: (5+5+2+5+7+8+2+8+3)/9 = 5 минут

• Между моментами освобождений: (16+12+1+1)/4 = 7,5 минут

Рассчитать среднее время для диаграммы 3 (1 клетка = 1 минута):

• Интервалов времени между поступившими заявками: (1+3+3+5+5+2+5+4+3+8+2+3+5+3)/14 = 3,71 минут

• Занятости всех приборов: (26+41+51+22+5+20+12+8+10)/9 = 21,67 минут

• Занятости 1-ого прибора: (26+22+20)/3 = 22,67 минут

• Между моментами занятий: (1+3+22+16+5+1+7+4)/8 = 7,38 минут

• Между моментами потерь: (2+5+7+8+2)/5 = 4,8 минут

• Между моментами освобождений: (16+5+1+7+4+6+2+1)/8 = 5,25 минут

• В очереди: (19+19+6+30+4+7)/6 = 14,17 минут

Часть 2.

1. Построить графики функции и плотности трех экспоненциальных распределений

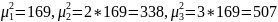
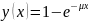– функция экспоненциального распределения

Графики функций экспоненциальных распределений изображены на рис. 1.

Зелёный:

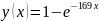
Синий:

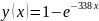
Красный: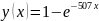

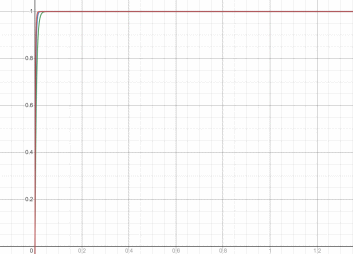
Рисунок 1 – Графики функций экспоненциальных распределений

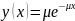– плотность экспоненциального распределения

Графики плотности экспоненциальных распределений изображены на рис. 2.

Зелёный:

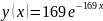
Синий:

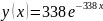
Красный: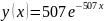

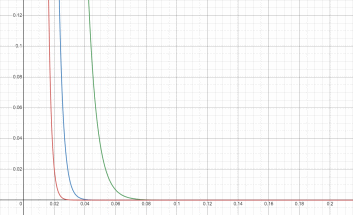
Рисунок 2 – Плотности экспоненциальных распределений

Можем сделать вывод, что чем больше µ, тем больше вероятность

малых значений случайной величины.

2. Построить графики плотности двух гиперэкспоненциальных распределений.

Формула:

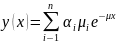
Весовые коэффициенты экспоненциальных распределений для первого и второго гиперэкспоненциальных распределений, соответственно:

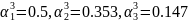
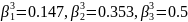
Графики плотности гиперэкспоненциальных распределений изображены на рис. 3.

Зелёный:

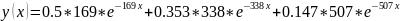
Синий: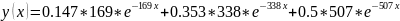

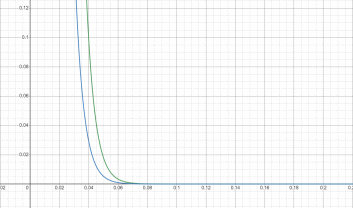
Рисунок 3 – Графики плотности двух гиперэкспоненциальных распределений

3. В этих же осях, что и графики п. 3, построить график плотности экспоненциального распределения

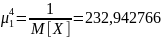
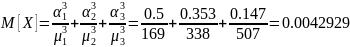
На рис. 4 изображены графики плотности гиперэкспоненциальных распределений.

Зелёный:

Синий:

Красный:

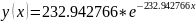
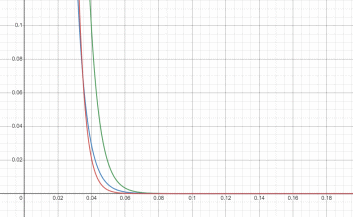
Рисунок 4 – Графики плотности трёх гиперэкспоненциальных распределений

Из полученных результатов можно сделать вывод, что меньше вероятность больших значений случайных величин, когда доля больше больших интенсивностей. Если сравнивать виды распределений, то у гиперэкспоненциального распределения меньше вероятность больших значений случайных величин.

4. Построить графики плотности трех нормированных эргалановских распределений, отличающихся рангом

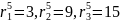
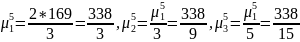
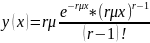– функция нормированного эргалановского распределения

Графики функций нормированных эргалановских распределений, отличающихся рангом, изображены на рис.5

Зелёный:

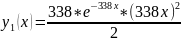
Синий:

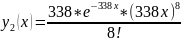
Красный:

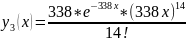
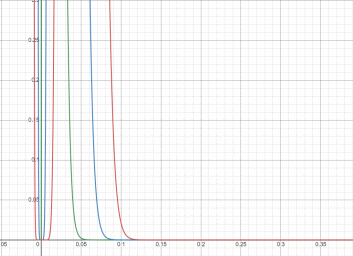
Рисунок 5 – Графики плотности трех нормированных эргалановских распределений

Можно сделать вывод, что с увеличением ранга вероятность больших значений уменьшается.