
Электроника и схемотехника, учебное пособие, Щ.А.С., О.А.Г
..pdf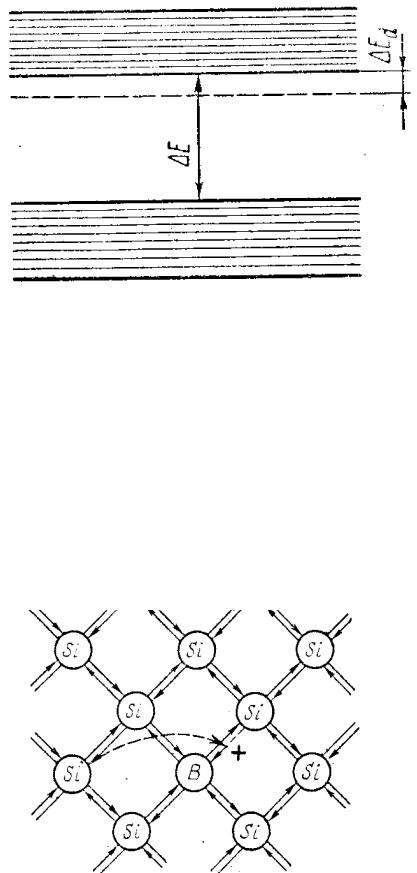
81
Рис. 5.5
Энергия Ed, необходимая для перехода электрона с уровня примеси в зону проводимости, меньше, чем энергия перехода электрона из валентной зоны E. Благодаря этому при невысоких температурах концентрация электронов, поставляемых примесными атомами в зону проводимости, значительно превышает концентрацию собственных носителей и проводимость полупроводника определяется примесными носителями (примесная проводимость). Атомы примеси получили название донорных, или просто доноров.
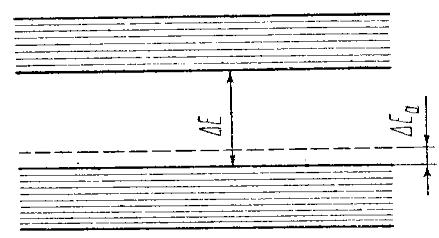
Если четырѐхвалентный атом Si замещѐн атомом элемента III группы периодической системы (например, бором), то трѐх его валентных электронов не хватает для заполнения валентных связей с соседними атомами, образуется валентная связь (рис. 5.6), которая может быть заполнена за счет перехода в вакансию электрона из любой соседней заполненной связи.
Рис. 5.6
82
Переход электрона из заполненной связи в вакантную, с энергетической точки зрения, представляет собой переход электрона из заполненной валентной зоны кристалла на локальный уровень примеси (рис. 5.7).
Рис. 5.7
Этот переход освобождает один из уровней в верхней части валентной зоны, тем самым создавая в кристалле дырку. Переход электронов из валентной зоны на уровни примеси требует меньшей энергии, чем переход их в зону проводимости (ΔEp , E). Атомы примеси такого рода называются акцепторными, или просто акцепторами.
Очевидно, что при наличии в кристалле доноров, кристалл имеет электронную проводимость, так как основной массой носителей заряда в нем будут электроны. При наличии в кристалле акцепторов проводимость кристалла - дырочная.
Те же правила определения знака примесной проводимости что и для полупроводников — элементов IV группы периодической системы, действуют и для полупроводниковых соединений элементов III и V групп периодической системы (соединений AIIIBV).
Примесные носители создаются в кристалле полупроводника не только чужеродными атомами, но и собственными атомами в том случае, если они оказываются в междоузлии. Так, переход атома Si в междоузлие вызывает образование двух локальных энергетических уровней: атом в междоузлии действует как донор, а пустой узел - как акцептор.
В полупроводниковых соединениях избыточные по отношению к стехиометрическому составу атомы тех самых элементов, из которых построена основная решетка, занимающие «неправильные» положения, являются либо донорами, либо акцепторами в. зависимости от того, какой из атомов соединения оказывается «нарушителем». Так, если полупроводник представляет собой соединение металла и металлоида (окислы, сульфиды и др.), то избыток атомов металла (по отношению к стехиометрическому составу) создает в полупроводнике электронную проводимость, избыток же атомов металлоида - дырочную проводимость.
Если в примесный полупроводник, обладающий электронной проводимостью, ввести

83
акцепторные примеси, то они будут захватывать электроны, уменьшая тем самым концентрацию примесных носителей заряда. То же самое происходит и при введении донорных примесей в примесный полупроводник с дырочной проводимостью. В полупроводниках с донорной примесью удельная проводимость вычисляется по формуле
n |
qe n un |
, |
(5.2) |
|
|
|
а в полупроводнике с акцепторной примесью –
p |
qe n u p |
, |
(5.3) |
|
|
|
где un и up - подвижности донорных и акцепторных примесей
5.1.3. РАВНОВЕСНЫЕ КОНЦЕНТРАЦИИ СВОБОДНЫХ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКЕ
В нормальном состоянии T = 0° К в полупроводнике нет свободных носителей заряда: все энергетические уровни в зоне проводимости свободны, а все уровни валентной зоны заняты электронами. Во всех процессах, которые мы будем рассматривать, участвуют электроны, расположенные на нижних уровнях.зоны проводимости, на верхних уровням валентной зоны и на локальных уровнях примеси, лежащих в запрещенной зоне кристалла.
Вероятность заполнения электроном энергетического уровня определяются функцией Ферми
f n (E) |
|
1 |
|
. |
|
|
|
|
(5.4) |
||
|
E E |
|
|||
|
|
|
|
|
|
|
e |
kT |
1 |
|
|
Вероятность того, что энергетический уровень E не занят электроном, определится в соответствии с формулой (5.4) так:
f p (E) 1 f n (E) |
|
1 |
|
. |
|
|
|
|
(5.5) |
||
|
E E |
|
|||
|
e |
|
1 |
||
|
kT |
|
|||
|
|
|
|
|
|
Если рассматривать энергетические уровни вблизи потолка валентной зоны, то вакантный уровень здесь эквивалентен свободной дырке и потому fp (E) в формуле (5.5) следует рассматривать как вероятность того, что энергетический уровень Е занят дыркой.
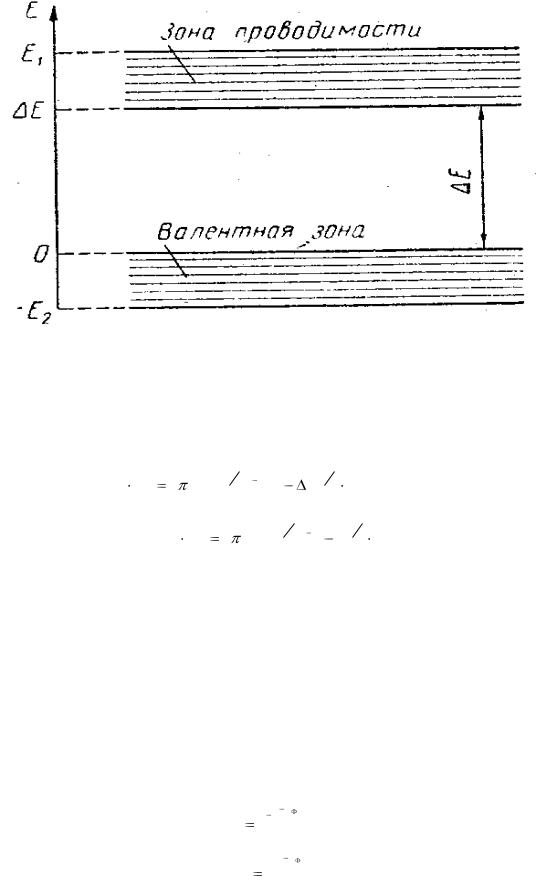
Так как величины функций fn (E) и fp (E) определяются в конечном счѐте разностью энергий (Е-ЕФ ), то для их вычисления не нужны абсолютные значения Е и ЕФ, необходимо только, чтобы обе эти величины отсчитывались от одного начала отсчѐта. За начало отсчѐта энергии будем принимать потолок валентной зоны (рис. 5.8).
84
Рис. 5.8
Распределение энергетических, уровней в нижней части зоны проводимости Rn(E) dE и в верхней части валентной зоны Rp(E) dE и с учетом системы отсчета (рис. 5.8) запишем:
R (E) dE 4 (2m ) 32 h |
3 (E E) 12 dE, |
(5.8) |
||
n |
n |
|
|
|
|
|
|
||
|
R (E) dE 4 (2m ) 32 h 3 ( E) |
12 dE, |
(5.9) |
|
|
P |
P |
|
|
|
|
|
||
где Rn(E) и Rp(E) - число уровней, приходящихся на единичный интервал энергий, в единичном объеме кристалла; mn и mp - массы доноров и акцепторов в объеме кристалла; h - постоянная Планка.
Если ширина запрещенной зоны в полупроводнике E>>kT, то вероятность перехода электрона из валентной зоны в зону проводимости очень мала, а следовательно, очень малы и fn (E) - вероятность заполнения уровней зоны проводимости электронами и fp(E) - вероятность заполнения уровней валентной зоны дырками. Если fn (E)<<1 и fp (E)<<1, то это значит, что в формулах (5.4) и (5.5) можно пренебречь единицей по сравнению с экспонентой и тогда эти выражения превратятся в следующие:
|
|
|
|
|
E |
E |
(5.10) |
||
f |
n |
(E) |
e |
kT |
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E E |
(5.11) |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
f |
p |
(E) |
e |
kT |
, |
|||
|
|
|
|
|
|
|
|
|
|
Полученные равенства (5.10) и (5.11) представляют собой функцию распределения
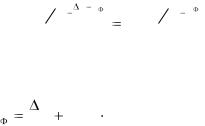
85
Больцмана. Эта функция, как известно, выражает распределение по энергиям частиц классического идеального газа. При небольших концентрациях свободных электронов и дырок, с которыми мы имеем дело в полупроводнике, эти частицы образуют невырожденные электронный и дырочный газ, свойства частиц которых подобны свойствам классического идеального газа.
В собственном полупроводнике концентрация доноров и акцепторов одинакова (ni = pi), поэтому, приравняв правые части выражений (5.6) и (5.7), получим
(m ) 3 |
|
E E |
|
|
) 3 |
|
E |
|
2 e kT |
(m |
p |
2 e kT . |
|||||
n |
|
|
|
|
|
|
|
|
Откуда уровень Ферми в собственном полупроводнике равен
E |
E |
3 |
kT ln |
mp |
. |
|
||
|
|
|
|
(5.12) |
||||
2 |
4 |
mn |
||||||
|
|
|
||||||
|
|
|
|
|||||
При Т=00 К уровень Ферми в собственном полупроводнике проходит точно посередине запрещѐнной зоны. Но эффективные массы электронов и дырок в полупроводнике не равны, как правило, масса дырок выше массы электрона, и поэтому уровень Ферми в собственном полупроводнике расположен ближе к зоне проводимости и при повышении температуры смещается вверх.
Следует подчеркнуть, что понятие эффективной массы удобно и корректно лишь по отношению к кинетике носителей; его нельзя отождествлять с понятием массы в обычном смысле этого слова. Так, различие эффективных масс отнюдь не характеризует различие силы тяжести, Понятие эффективной массы вне зависимости от положения электрона в энергетической зоне) наглядно иллюстрируется функциями W (р), где W - энергия и р =
mv — импульс электрона (обычно вместо импульса используется пропорциональный ему квазиимпульс или волновое число k =2πp/h, где h – постоянная Планка.
Для получения функции W (р) нужно так или иначе смоделировать кристаллическую решетку, отразив наличие внутренних полей и взаимодействия электронов и атомов. В результате зависимость W (р) оказывается набором периодических функций, которые для простейшего одномерного случая показаны на рис. 5.9. Каждый периодический компонент соответствует разрешенной зоне, а «расстояние» между минимумами и максимумами смежных компонентов — запрещенной зоне. С ростом энергии ширина разрешенных зон увеличивается, а ширина запрещенных зон уменьшается, что соответствует интерпретации зон на рис. 5.8.
Каждый периодический компонент соответствует разрешенной зоне, а «расстояние» между минимумами и максимумами смежных компонентов — запрещенной зоне. С ростом энергии ширина разрешенных зон увеличивается, а ширина запрещенных зон уменьшается, что соответствует интерпретации зон на рис. 5.8.
Воспользуемся кривыми W(p) для анализа эффективной массы. Как известно, кинети-

86
ческая энергия электрона может быть записана в виде
W |
mv 2 |
|
p 2 |
. |
|
2 |
|
2m |
(5.13) |
||
|
|
|
|||
|
|
|
|
Рис. 5.9
Если т = const (электрон в вакууме), то W ~ р2, как показано на рис. 5.9 пунктирной параболой. В твердом теле функция W (р) описывается кусочной кривой, показанной жирными линиями; эта кривая отличается от параболы и наличием разрывов. и формой непрерывных участков; следовательно, в твердом теле т ≠ =const. Дифференцируя дважды функцию W (р), можно определить эффективную массу электрона как
|
1 |
|
h |
2 |
1 |
m |
|
|
|||
|
|
|
|
|
|
d 2W / dp2 |
2 |
|
d 2W / dk 2 |
||
|
|
||||
и проследить за еѐ изменениями с помощью кривых W(p). Для всех зон результат будет один и тот же; ограничимся нижней зоной рис. 5.9.
Между точками а и б имеем d2W/dp2>0, т. е. m* >0, что соответствует «обычному» электрону. Между точками б и в имеем d2W/dp2<0, т. е. m* <0, что соответствует электрону с отрицательной массой. Наконец, в точке перегиба б имеем d2W/dp2=0, т. е. m* = ∞, и значит (при конечном импульсе р), скрорость обращается в нуль; это соответствует ранее отмеченному «резонансу» между электронной волной и решѐткой.
В начальной и конечной точках кривой (вблизи минимума и максимума) функция d2W/dp2 близка к квадратичной параболе, поэтому на этих участках значения кривизны почти постоянны, а значит почти постоянны и эффективные массы, однако они различаются не только по знаку, но и по значению.
5.1.4. ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖЕНИЕ СВОБОДНЫХ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКЕ
87
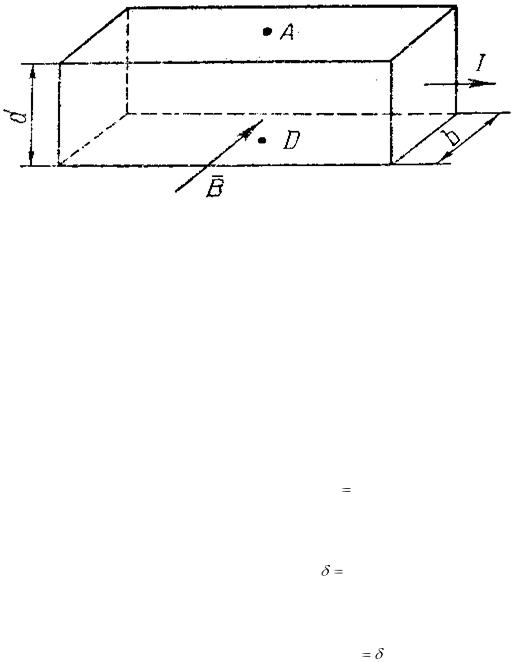
Изучение свойств полупроводника начинается по существу с определения знака и концентрации носителей заряда. Наиболее распространенным методом измерения концентрации и знака носителей заряда в проводнике является метод измерения напряжения Холла. Пусть по проводнику, имеющему форму прямоугольного параллелепипеда (рис. 5.10), протекает электрический ток. В этом случае на противоположных гранях, параллельных направлению тока, всегда можно найти две точки A и D, лежащие на одной эквипотенциальной поверхности. Напряжение между этими точками Ux = 0.. Если же проводник поместить в магнитное поле, вектор индукции которого В перпендикулярном направлению тока и боковым граням образца, то между точками A и D возникает напряжение, т. е. Ux ≠ 0. Причиной этого явления, получившего название эффекта Холла, является сила Лоренца, т. е. сила, действующая на электрический заряд, движущийся в магнитном поле.
Рис. 5.10
В общем случае сила Лоренца F равна
F=e[vB],
где q – заряд носителя, В – магнитная индукция, v - скорость дрейфа носителя. В случае, изображенном на рис. 5.10, под действием, силы Лоренца носители заряда будут смещаться, заряжая верхнюю и нижнюю грани зарядами противоположного знака. В образце появится поперечное электрическое поле. Смещение зарядов будет продол;аться до тех пор, пока сила Лоренца не уравновесится силой поперечного электрического поля, действующей на носители заряда в направлении, противоположном силе Лоренца, т. е.
Ex q qvB, |
(5.14) |
|
Учитывая, что плотность тока
qnv, |
(5.15) |
|
перепишем формулу (5.14) так:
Ex qn B |
(5.16) |
|

88
|
Ex |
|
1 |
|
B. |
|
|||
или |
|
|
|
|
|
(5.17) |
|||
|
qn |
||||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
С другой стороны, |
|
|
|
|
|
|
|
|
|
E |
|
|
|
U x |
. |
|
||
|
x |
|
(5.18) |
||||||
|
|
|
|
d |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
Из выражений (5.17) и (5.18) следует |
|
|
|
|
|
|
|
|
|
U x |
|
1 |
|
Bd. |
|
|||
|
|
|
|
|
|
|
(5.19) |
||
|
|
|
qn |
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Если в формуле (5.31) заменить плотность тока δ величиной тока I, то для холловской разности потенциалов получим
IB |
|
U x Rx b , |
(5.20) |
где Rx= (qn)-1 - коэффициент Холла.
Для полупроводника со смешанной проводимостью (электронной и дырочной) коэффициент Холла равен
Rx |
3 |
|
pu 2p |
nun2 |
|
|
|
|
|
|
|
|
|
|
|
8q |
|
( pu p |
nun ) |
2 . |
(5.21) |
||
|
|
||||||
|
|
|
|
|
|||
Определив из опытных данных коэффициент Холла Rx, можно вычислить концентрацию носителей заряда в полупроводнике. Заметим, что знак холловской разности потенциалов зависит от знака носителей заряда в полупроводнике.
5.1.5. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ПРОВОДИМОСТИ ПОЛУПРОВОДНИКА
Проводимость всякого проводника пропорциональна концентрации свободных носителей заряда в нем и их подвижности. Следовательно, температурный ход проводимости полупроводника определяется температурной зависимостью концентрации и подвижности носителей в нем. Концентрации носителей заряда в полупроводнике зависит от температуры [5]. Подвижность свободных носителей в кристалле определяется рассеянием электронных волн на неоднородностях кристаллической решетки.
В кристалле эти неоднородности могут быть двух типов: дефекты кристаллической решетки (атомы примесей, отклонение от стехиометрии. дислокации, трещины, границы кристаллических зерен н т. п.) и флуктуационные неоднородности, возникающие на тепловых колебаниях решетки. Одни и те же неоднородности по-разному сказываются на рассеянии носителей заряда в металле и в полупроводнике. Так как в металле скорость электронов благодаря вырождению на порядок выше, чем в полупроводнике, длина электронной долин: в металле соответственно на порядок меньше, чем в полупроводнике. Не-
89
однородности атомных размеров вызывают в металле значительное рассеяние, в то время как в полупроводнике это рассеяние очень мало.
В атомных полупроводниковых кристаллах тепловое рассеяние значительно при сравнительно высоких температурах. При низких температурах преобладает рассеяние на примесях. При наличии обоих механизмов рассеяния результирующая подвижность u может быть представлена в виде
|
|
1 |
|
|||
u |
1 |
1 |
|
|
||
|
|
|
|
|
||
uпр |
, |
(5.22) |
||||
|
||||||
|
|
ut |
|
|||
где uпр - подвижность носителей заряда при рассеянии только на примесях, uт - подвижность носителей при рассеянии и только на тепловых колебаниях.
Эти две составляющие подвижности носителей по разному зависят от изменения температуры. Теоретический расчѐт показывает, что
uпр~T3/2, а uт~T-3/2.
Отсюда температурный ход подвижности носителей заряда можно представить в виде
|
3 2 bT |
3 |
|
1 |
|
u aT |
2 |
. |
(5.23) |
||
|
|
|
|
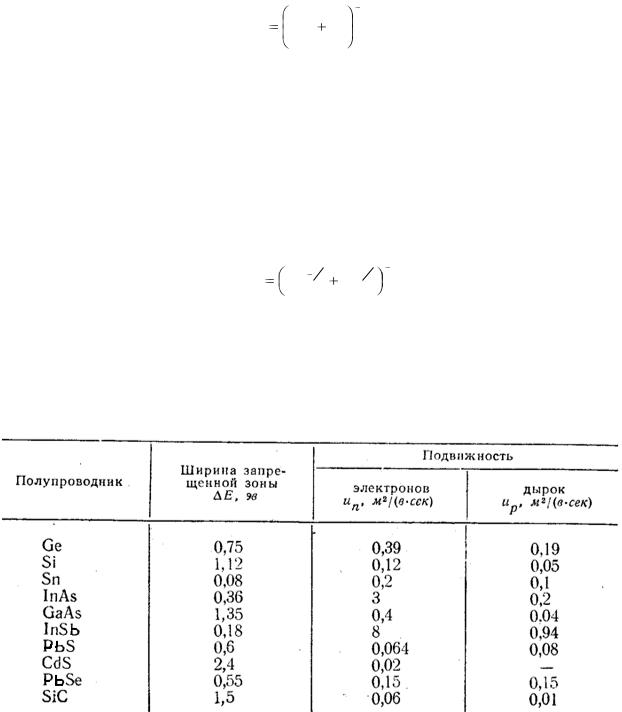
В табл. 5.1 приведены основные величины, характеризующие полупроводники: ширина запрещѐнной зоны E и подвижности носителей заряда un и up . Все эти величины даны для температуры 25 оС.
Таблица 5.1
Зная температурную зависимость концентрации свободных носителей заряда и их подвижности (5.23), можно утверждать, что температурный ход проводимости полупро-
90
водника определяется в основном экспоненциальным множителем в формулах (5.10) и (5.11), поэтому удельная электропроводность полупроводника может быть выражена следующей формулой:
γ = γсоб + γпр =С1е- Е/2kT +C2e- Eпр/2kT, |
(5.24) |
где γсоб и γпр – удельные электропроводности, обусловленные собственными и примесными носителями заряда, E – ширина запрещѐнной зоны полупроводника, Eпр – энергия, необходимая для создания примесного носителя заряда, С1 и С2 – коэффициенты, зависящие от природы полупроводника и очень слабо зависящие от температуры.
При сравнительно низких температурах можно пренебречь первым слагаемым в формуле (5.24), а при высоких, когда наступает примесное истощение, - вторым. В первом случае удельная электропроводность будет равна
- |
E |
/2kT |
(5.24,а) |
γпр = C2e |
пр |
, |
во втором –
γсоб = С1е- Е/2kT. |
(5.24,б) |
Анализировать температурную зависимость проводимости полупроводника удобно с помощью графика этой зависимости, полученного в полулогарифмической системе координат. Прологарифмировав формулы (5.38,а) или (5.38,6), мы получим выражение типа
lnγ = lnC - E/2kT. |
(5.25) |
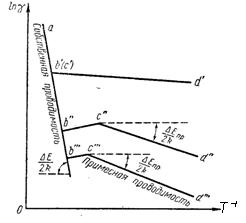
Если по оси абсцисс отложить обратную температуру Т-1, а по оси ординат –lnγ, то график зависимости проводимости полупроводника от температуры будет иметь вид ломаной линии (рис. 5.11).
Рис. 5.11
В области низких температур в полупроводнике имеет место примесная проводимость (участки d’’’- c’’’ и d’’- c’’) увеличение которой в зависимости от температуры определяется возрастанием концентрации примесных носителей заряда. Участки c’’’- b’’’и c’’-
