Электроника и схемотехника, учебное пособие, Щ.А.С., О.А.Г

391

чтобы выбранный функционал принимал минимальное значение. Здесь - множество состояний предельного цикла периодического решения уравнения (8.127).

Поставленную задачу оптимального управления для вырожденных автоколебательных систем можно будет считать решенной, если будут определены условия существования, период и число интервалов оптимального предельного цикла, определена его область притяжения, а также дано решение задачи синтеза, т. е. определено управление в функции

положения фазовой точки g(t) f (u) .

Если оптимальный предельный цикл существует в вырожденной автоколебательной системе, то он имеет два интервала знакопостоянства управления независимо от структуры системы.. Для выделения этих двух интервалов введем дискретную перемев-

шую s , принимающую значение «1» во время подпитки РГН от источника питания, и значение «0» -в.режиме диссипации электрической энергии.

Выбор оптимального закона управления во время подпитки РГН от источника питания сделать нетрудно. Любая система стремится к минимуму потребления мощности на управление и к минимальной разности между заданным режимом и действительным значением фазовой координаты. Учитывая, что наша автоколебательная система вырожденная, запишем искомый функционал в скалярной форме

где f , q и r - в общем случае некоторые функции времени, но для упрощения будем их считать постоянными.

Как уже указывалось ранее, работа коммутирующего устройства, управляющего процессом заряда конденсатора, начинается в момент времени, равный нулю, и заканчивается

в момент времени t 1 . Этим обусловлен выбор пределов интегрирования в формуле

(8.128).

Найдя решение уравнения (8.128), определим оптимальную форму переходного процесса во время заряда конденсатора. Определение основных параметров предельного цикла (частоты, амплитуды, формы сигнала и т.д.) требует нахождения минимума функционала вида

где Т – период автоколебаний РГН.

394

Определим параметры оптимального предельного цикла [21]. Для чего воспользуемся методом припасовывания (точечных отображений) L3IJ. Определим переходные процессы заряда-разряда конденсатора С (рис. 8.23), если рассматривать РГН как устройство, оптимальное по быстродействию, установившимся режимом которого будет предельный цикл вырожденной автоколебательной системы [21].

Для нахождения параметров оптимального по быстродействие переходного процесса воспользуемся принципом максимума Л.С.Понтрягина [18]. Используя дискретную переменную s, можно записать следующую систему уравнений:

где s – дискретная переменная.

Найдѐм минимум функционала (8.129) для вырожденной автоколебательной системы, описываемой, описываемой системой уравнений (8.138). Решением поставленной задачи будет закон изменения управляющего воздействия s во времени, который бы удовлетворяло ограничениям, накладываемым на параметры предельного цикла, и обеспечивал пе-

ревод системы (8.138) в область за минимальное время.

Если оптимальное управление s существует, то этому управлению должен соответствовать вектор сопряжѐнных переменных. Гамильтониан для рассматриваемой системы (8.138) представим в виде

где p1 - сопряжѐнная переменная, которую можно определить, решив дифференциальное уравнение

После соответствующих подстановок и интегрирования уравнения (8.140), получим

где p10 const .

396

ными интегральными формулами. Далее будем рассматривать функцию модуля, причѐм будем пользоваться квадратом модуля, а не самим модулем, так как это проще. Очевидно, если функция модуля дана, еѐ можно возвести в квадрат. Мы полагаем, что квадрат модуля задан в виде рациональной функции от s, а, не в виде кривой, для которой нужно найти приближенное выражение.

Допустим теперь, что дана рациональная функция от ω, скажем, G( j ) , удовлетворяющая необходимым условиям, при которых она является квадратом модуля функции цепи. Эти условия таковы: функция должна быть чѐтной функцией от ω, а степень числителя еѐ не выше степени знаменателя больше, чем на два, так как передаточная функция не может иметь больше одного простого полюса в бесконечности. Кроме того, если

G( j ) имеет конечные полюсы на оси j, они должны быть двукратными, так как полюсы

Будем разлагать числитель и знаменатель функции G ( s ) на множители. Некоторые из них нужно включить в F(s), а другие в F(-s). Сначала найдем, какое будет расположе-

ние нулей и полюсов функции G(s). Напомним, что G ( s ) есть отношение, двух четных многочленов.

Теперь возникает вопрос, как выбрать полюсы и нули функции F(s) из полюсов и ну-

лей функции G(s). Для полюсов ответ простой. Мы знаем, что F(s) должна быть регулярна в правой полуплоскости. Поскольку полюсы функции F(-s) равны полюсам функции F(s) с противоположным знаком, то функция F(-s) регулярна в левой полуплоскости. Следовательно, распределение полюсов функции G(s ) может быть однозначным : п о -

люсы G(s ) в левой полуплоскости

луплоскости принадлежат F(-s). Полюсы на оси j распределены равномерно. Они явля-

ются двукратными в функции G ( s ) и простыми в функциях F(s), и F(-s). Распределение

397

нулей приведено на рис. 8.13. Такая симметрия распределения нулей называется квадратной симметрией. Говорят, что полюсы и нули передаточной функции G(s ) или квадра-

та модуля функции распределены симметрично по квадратам.

Что касается выбора нулей, то он не столь прост. Если F(s) не является входной функцией, то условие, что она не должна иметь нулей в правой полуплоскости, не обязательно. Поэтому не обязательно приписывать функции F(s) все нули функции

G ( s ) , расположенные в левой полуплоскости. Но если задано, что F(s) должна быть функцией минимальной фазы, то все нули функции G(s), расположенные в левой полу-

плоскости, следует приписать F(s). Если это условие не задано, то функции F(s) можно приписать некоторые нули правой полуплоскости. Однако надлежит помнить, что пара комплексных нулей должна быть объединена, так как F(s) должна быть действительной функцией от s. Итак, F(s) однозначно определяется функцией G(s) только в том случае, если F(s) должна быть функцией минимальной фазы.

Наконец, нули на оси j следует разделить поровну между F(s) и F(-s), так же как полюсы.

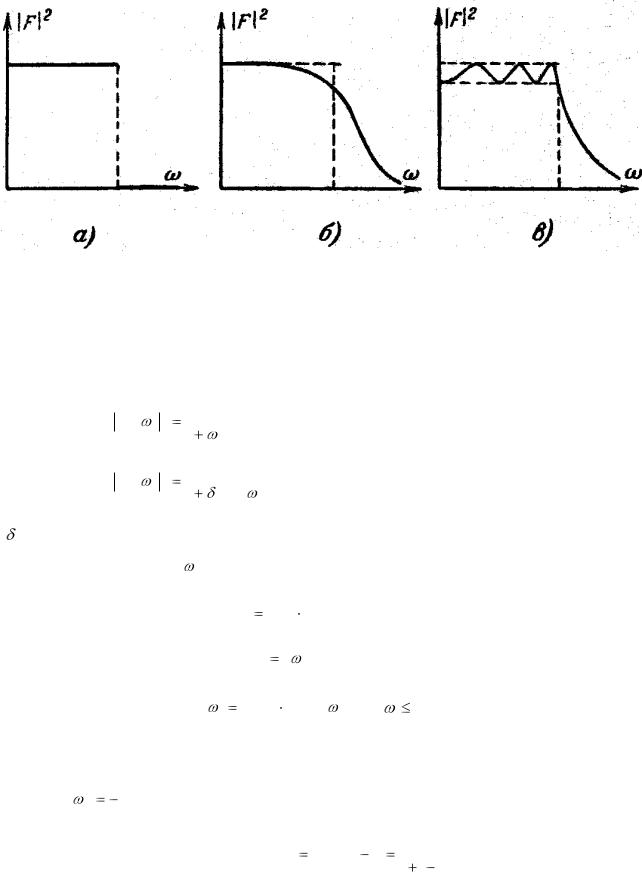
Разберем теперь для пояснения этого метода несколько примеров; имеющих практическое значение. Для обычных электрических фильтров требуются передаточные функции, имеющие совершенно постоянные модули на оси j в данном интервале частот, который называется полосой пропускания, и в точности равные нулю на остальной оси j , в так называемой полосе задерживания. Модуль рациональной функции на оси j не может иметь такую идеальную форму. Однако можно найти передаточные функции, модули которых на оси j так или иначе приближаются, к желаемой функции.

' Рассмотрим передаточную функцию идеального фильтра нижних частот, изображенную на рис. 8.24, а. На рис. 8.24, б, в показаны два способа приближенной реализации этой идеальной функции. Первый способ называется максимально гладкой аппроксимаци-

ей или аппроксимацией Баттерворта, а второй; способ - равноволновой аппроксимацией

или аппроксимацией. Чебышева. Максимально гладкая аппроксимация монотонна в полосе пропускания и в полосе задерживания, причем максимальная ошибка получается вблизи границы полосы пропускания. Аппроксимация Чебышѐва является осциллирующей в полосе пропускания, причѐм пики волн одинаковы. Благодаря этому ошибка распределена в полосе пропускания более равномерно.

399

тель. В данном случае это выполняется сравнительно просто. Нули знаменателей находятся из выражения

Передаточная функция F(s) в этом случае принимает следующий вид:

Найденная функция F(s) имеет вид, представленный на рис. 8.24, б.

Рассмотрим реакцию, вызванную аппроксимацией Чебышѐва (8.150). Чтобы найти полюсов, заменим j на s и приравняем знаменатель нулю. Получим

Если в последнем уравнении раскрыть ch(n·w) и приравнять вещественные и мнимые части этого выражения нулю, то получатся значения х и у, удовлетворяющие этому урав-

Последние выражения можно объединить, произведя обычные операции