
Электроника и схемотехника, учебное пособие, Щ.А.С., О.А.Г
..pdf
311
X ( j 1) AX( j) . |
(7.4) |
Отсюда после m тактов новое состояние будет
X ( j 1) Am X ( j) . |
(7.5) |
Учитывая периодичность генерируемого сигнала, то при m = N (периоду генерируемой последовательности), должно выполняться следующее условие:
Am E , |
(7.6) |
где E - единичная матрица.
Обычно последовательность описывают характеристическим уравнением или характеристическим полиномом. Характеристическое уравнение определяется следующим образом:
|
F( |
) |
|
A |
E |
, |
|
|
(7.7) |
|
где - двоичная переменная. |
|
|
|
|
|
|
|
|
|
|
Следовательно, характеристическое уравнение имеет вид: |
|
|||||||||
|
|
n |
|
|
|
|
|
|
|
|
F ( |
) |
c |
k |
n k , c |
0 |
c |
1. |
(7.8) |
||
|
|
|
|
|
|
1 |
|
|
||
|
k |
0 |
|
|
|
|
|
|
|
|
Характеристический полином |
|
f ( |
) определяется по формуле |
|
||||||
|
|
n |
|
|
|
|
|
|
|
|
f ( |
) |
|
c |
k |
k , c |
0 |
c |
1. |
(7.9) |
|
|
|
|
|
|
1 |
|
|
|||
|
|
k 0 |
|
|
|
|
|
|
|
|
Решение широкого круга задач в области схемотехники связано с использованием множества сигналов, обладающих следующими свойствами:
-каждый из сигналов данного множества легко отличим от своей сдвинутой во времени копии, то есть должен иметь автокорреляционную функцию (АКФ) с малыми значениями боковых выбросов;
-каждый из сигналов данного множества легко отличим от любого другого сигнала этого множества, то есть взаимно-корреляционная функция (ВКФ) любой пары несовпадающих сигналов множества должна быть минимальной;
-множество используемых сигналов должно составлять достаточно обширный ан-
самбль.
Этими свойствами обладают последовательности Голда, используемые для широкополосных сетей связи. Основой для построения последовательности Голда являются М- последовательности, обладающие хорошими автокорреляционными свойствами [9-12]. М- последовательности – это линейные рекуррентные двоичные последовательности n -ного
порядка, которые имеют максимальное значение минимального периода T 2n |
1. Число |
|||
элементов в периоде T (длина N М-последовательности) определяется по формуле (7.1). |
||||
Число М-последовательностей LN |
степени n совпадает с числом примитивных |
|||
многочленов степени n. Число LN можно найти по формуле [1]: |
|
|||
LN |
(N ) |
, |
(7.10) |
|
|
||||
log 2 (N 1) |
||||
|
|
|
||
где (N ) - функция Эйлера, определяемая, как число взаимно простых чисел с N |
2n 1; |
|||
Каждая М-последовательность имеет свой номер [9, 11]. Максимально возможный период М-последовательности равен 2n -1. Примитивным называется многочлен, степени которого образуют все элементы М-последовательности. Номер М-последовательности совпадает с номером примитивного многочлена, являющегося характеристическим многочленом М-последовательности. Из соответствующих таблиц [9.11] для многочлена степени n =6 имеются многочлены с номерами 1, 3 и 5, для которых указаны характеристические многочлены: 103F=1000011, 127B=1010111 и 147Н=1100111. Для определения неприводимых многочленов, соответствующих ненулевым элементам начальной ячейки

312
сдвигового регистра, использованы буквы E, F, H, буквы A, B, C и D указывают на то, что указанные многочлены являются непримитивными.
Чтобы получить М-последовательность с другим номером используют децимацию исходной М-последовательности. Децимация последовательностиэто циклическая пере-
становка номеров элементов исходной m-последовательности i |
по правилу [9]: |
j (q i) mod N , |
(7.11) |
где q - индекс децимации, j .- номер элемента результирующей m-последовательности. Если индекс децимации q исходной М-последовательности взаимно прост с еѐ
длиной N , то длина результирующей М-последовательности будет равна исходной. В противном случае результирующая М-последовательность будет состоять из фрагментов меньшей длины [9]. При этом номер результирующей М-последовательности r находится из выражения:
r (q p) mod N , |
(7.12) |
где p - номер исходной М-последовательности.
Если в качестве исходного значения взять полином с номером 1 (103F), который является примитивным, то взяв индекс децимации q =3, получим М-последовательность,
соответствующую полиному с номером 3, т. е. 127В.
Заметим, что полином 127В является непримитивным, а НОД(63,3)=3≠1. Следовательно, длина результирующей последовательности будет N 63/ 3 21.
Если взять индекс децимации q =5, получим m-последовательность, соответствующую полиному с номером 5, т. е. 147Н. Так как НОД(63,5)=1, то длина результирующей последовательности будет равна исходной, т. е. N 63, а полученная последовательность будет максимальной длины, т. е. М-последовательностью.
Для описания выходной последовательности сдвигового генератора используют производящую функцию. Определим выходную последовательность в виде
am |
a0 , a1 , a2 ,... |
, |
(7.13) |
где индекс m означает момент времени; то есть, a0 |
появляется вначале, затем a1 |
и так да- |
|
лее. |
|
|
|
Отметим, что начальные условия не влияют на выходную последовательность сдвигового регистра, поскольку начало предполагается, как время, когда начальные условия уже будут выведены из регистра сдвига. Тогда производящая функция выходной последовательности G(x) задается в виде
G(x) |
ak x k , |
(7.14) |
k |
0 |
|
Начальное состояние регистра сдвига определяется как a 1 , a 2 , a 3 ,..., a n 1 , a n . То- |
||
гда выходная последовательность a0 , a1 , a2 ,... определяется линейным рекуррентным соотношением
|
n |
|
am |
ci am i , m 0,1,2,..., |
(7.15) |
|
i 1 |
|
Так что последовательность определяется начальными условиями при синхронизации регистра. Подставляя (7.14) в формулу (7.13), получим
|
|
n |
|
|
G(x) |
|
|
ci ak i x k , |
(7.16) |
|
k 0 |
i |
1 |
|
Изменяя порядок суммирования, получим |
|
|
|
|
n |
|
|
|
|
G(x) |
ci xi |
|
ak i x k i |
или |
i |
0 |
k |
0 |
|
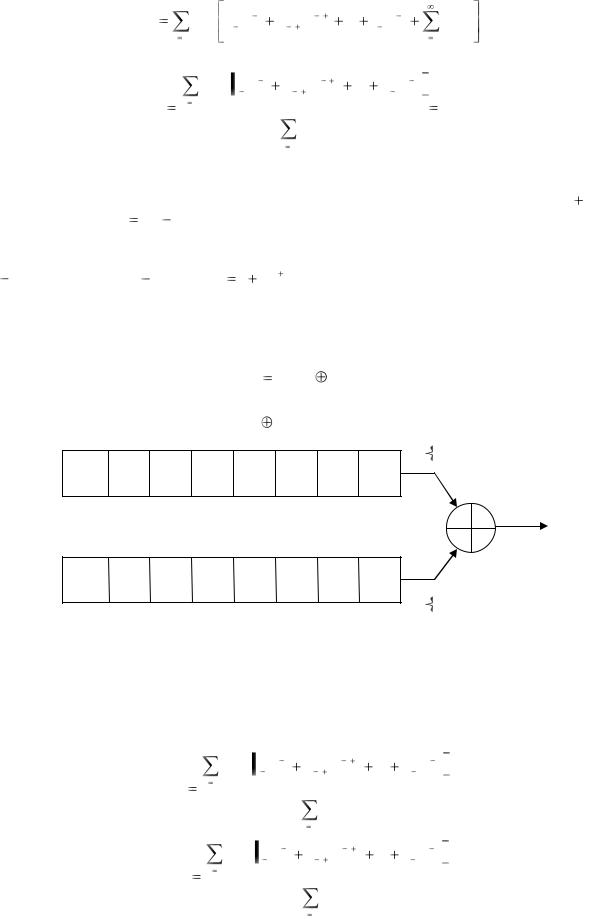

314
|
n |
|
|
|
|
|
|
ci xi (a i |
b i )x i (a i 1 |
b i 1 )x i 1 ... (a 1 |
b 1 )x 1 |
|
|
G1 (x) |
i 1 |
|
|
|
. |
(7.22) |
|
n |
|
||||
|
|
|
ci xi |
|
|
|
|
|
i |
0 |
|
|
|
Врезультате получается та же самая М-последовательность, но начальные условия определяются как поразрядная сумма по модулю 2 их начальных условий. Поэтому два сдвиговых регистра в этом случае можно заменить одним, но начальные условия формируются по первоначально сформулированному правилу.
Вслучае использования различных М-последовательностей для формирования кода Голда, то необходимо найти предпочтительные пары. Первую М-последовательность выбирают, исходя из условия, что она описывается примитивным двоичным полиномом степени n . Для выбора предпочтительных пар существуют следующие правила. Если для формирования последовательности Голда используются сдвиговые регистры длины N , то
предпочтительная пара выбирается из М-последовательностей длины N 2n 1 . Одним из способов получения М-последовательностей является децимация исходной М- последовательности.
При выборе предпочтительных пар следует придерживаться следующих правил:
1. |
n 0 mod4, т. е., n либо нечетно, либо n 2 mod4; |
2. |
элементы второй последовательности b выбираются по правилу b a[q] ,, где q - |
индекс децимации. Для нечетного q любой, а для четного q индекс децимации выбирают, исходя из альтернативы:
q 2k 1, либо q 22k 2 , НОД n, k |
1, n |
2 j 1 |
, |
j 1,2,3,.... |
(7.23) |
|
2, n |
2 mod4 |
|
|
|
Необходимо найти предпочтительные пары М-последовательностей, представимых характеристическими полиномами степени n =10. При этом длина М-последовательности будет N 1023.
Из таблиц полиномов, приведенных в [9,10], выделим полиномы степени 10. Для удобства расположим указанные полиномы в виде диаграммы (рис. 7.31).
Выберем в качестве исходного полином с номером 1 – 2011E=10000001001. Этот полином примитивный, ему соответствует некоторая М-последовательность длиной
N 1023. Следовательно, можно сформировать 1025 последовательностей Голда. Выберем индекс децимации q =5. Для этого случая НОД(1023,5)=1. Следовательно,
последовательности Голда будут максимальной длины. В результате децимации по индексу q =5 полином с номером 1 переходит в полином с номером 5, т. е. 2415Е. Децимация
полинома с номером 5 по индексу 5 дает полином с номером 25, т. е. 2443F. А децимация полинома с номером 125 по индексу 5 дает полином с номером 625.
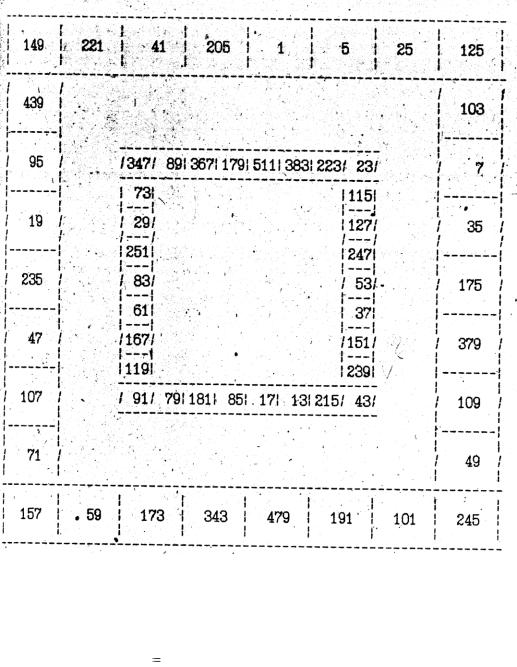
315
Рис. 7.31. Диаграмма расположения номеров полиномов для последовательности, генерируемой 10-разрядным сдвиговым регистром.
.Полином с номером 625 не существует [9.11]. Тогда поступают таким образом. Необходимо подобрать такое целое k , чтобы получился номер существующего в таблицах [9.10] полинома с номером r ( p  2k ) mod N . Для этого необходимо последовательно
2k ) mod N . Для этого необходимо последовательно
произвести вычисления, начиная с k =1, следующего вида: 625·2 mod1023=227, 227·2 mod1023=454, 454·2 mod1023=908, 908·2 mod1023=793, 793·2 mod1023=563, 563·2 mod1023=103.
Полином с номером 103 имеется в таблицах [9, 10]. Он равен 3575G=11105111105. Поэтому он будет составлять предпочтительную пару с полиномом с номером 125 для получения последовательности Голда.
Далее будем искать предпочтительный полином для полинома с номером 103. Умножив его номер на 5, получим 515. Полинома с таким номером нет в таблицах. Поэтому производим следующую операцию:
515·2 mod1023=7.

316
Полином с таким номером существует в таблицах [1,2]. Продолжая выполнять умножения, получим последовательно номера полиномов: 35, 175, … Последовательность найденных полиномов приведена на рисунке 3. Наконец, полином с номером 205 переходит в полином с номером 1025 mod1023=2. Такого полинома в таблицах [1,2] нет. Но если этот номер умножить на девятую степень 2, то получим 512·2 mod1023=1. А это номер исходного полинома. Следовательно, круг номеров полиномов, образующих предпочтительные пары, замкнулся. Следует отметить, что номера полиномов, различающихся на степени 2 по модулю длины последовательности, образуют один смежный класс. Поэтому полиномы с номерами 1 и 2 образуют один смежный класс, а перейти от номера 2 к номеру 1 можно было бы простым делением на два
Согласно формуле (7.2), число примитивных полиномов степени n =10 должно быть 60. Согласно рис. 7.31 найдено 30 полиномов. Но существуют как прямые, так и обратные полиномы. Причем все примитивные прямые полиномы имеют примитивные обратные полиномы. То же относится и к непримитивным полиномам.
Обратные полиномы к приведенным во внешнем квадрате указаны во внутреннем квадрате. Поэтому прямому полиному с номером 1 соответствует обратный полином с номером 511. Следовательно, следующим номером полинома по индексу децимации q =5 будет полином
511·5·28 mod1023=383.
Далее номера многочленов определяются аналогичным образом. В таблицах обычно приводится не все номера многочленов, но у каждого многочлена есть обратный. Поэтому следует постоянно проверять, есть ли в таблице обратный многочлен. В табл. 7.9 приведены все прямые и обратные многочлены степени 10.
|
|
|
Таблица 7.9 |
Прямые |
Обратные |
Прямые |
Обратные1 |
1 |
511 |
53 |
175 |
5 |
383 |
59 |
79 |
7 |
127 |
71 |
119 |
13 |
191 |
73 |
439 |
17 |
479 |
83 |
235 |
19 |
251 |
85 |
343 |
23 |
125 |
89 |
221 |
25 |
223 |
91 |
157 |
29 |
95 |
101 |
215 |
35 |
247 |
103 |
115 |
37 |
379 |
107 |
167 |
43 |
245 |
109 |
151 |
41 |
367 |
149 |
347 |
49 |
239 |
179 |
205 |
47 |
61 |
173 |
181 |
Не все получающиеся последовательности Голда обладают желаемыми спектрами. Голд [14] показал, что коды Голда можно разделить на три класса по балансу. Балансный код - это код, в котором число «единиц» превышает число «нулей» на единицу. Два других класса имеет превышение и недостаток «единиц». Голд показал, что для n нечетного число «единиц» и количество кодов с этим числом «единиц» эти случаи можно представить табл.7.2. Из данных табл. 7.2 видно, что в первом классе число «единиц» составляет 2n 1 , а число «нулей» на единицу меньше, что означает, что первый класс сбалансирован. Второй и третий классы явно несбалансированны. Чтобы сгенерировать сбалансированный код Голда, необходимо выбрать относительный сдвиг по фазе между исходными вы-

317
бранными m-последовательностями, т. е. предпочтительными парами.
Таблица 7.10
Класс |
Число «единиц» в последо- |
Число «нулей» в после- |
|
вательности |
довательности |
1 |
|
2n 1 |
2n 1 1 |
|
2 |
2n 1 |
2(n 1) / 2 |
2n 2 |
2(n 3) / 2 |
3 |
2n 1 |
2(n 1) / 2 |
2n 2 |
2(n 3) / 2 |
Определим характеристическую фазу последовательности. Особенностью характеристической фазы m-последовательностями является то, что когда она квантуется на каждом другом элементе исходной последовательности, то в результате получается та же m- последовательность. Пусть f (x) является характеристическим полиномом степени n не-
которой m-последовательности. Соотношением (17) можно представить любую фазу m- последовательности, где числитель g(x) является производящей функцией степени
меньшей, чем n .
В результате деления f (x) / g(x) получается формальный многочлен, двоичные коэффициенты которого являются элементами последовательности, генерируемой сдвиговым регистром. Формула для полинома g(x) , что определяет характеристическую фазу М-последовательности получена Голдом
g(x) |
d xf (x) |
, если f (x) нечетной степени; |
(7.24, а) |
||
|
|||||
|
dx |
|
|
|
|
g(x) |
f (x) |
d x f (x) |
, если f (x) четной степени. |
(7.24, б) |
|
|
|||||
dx
Дифференцирование производится обычным способом с учетом, что коэффициенты берутся по модулю 2.
Найдем относительную фазу, с которой должна суммироваться предпочтительная пара М-последовательностей, чтобы попасть в первый класс. Пусть a и b составляют предпочтительную пару М-последовательностей в их характеристической фазе. Если характеристический полином f (x) нечетной степени, то производящий полином имеет вид
G(x) |
|
1 c(x) |
, |
(7.25) |
|
1 d (x) |
|||||
|
|
|
|||
где степень d (x) составляет n , а степень c(x) |
- не выше n |
1 |
|||
Первым символом частного от деления по формуле (7.25) будет 1. Схема формирования последовательности Голда из двух М-последовательностей приведена на рис. 7.30. Далее опишем процедуру генерации сбалансированных кодов Голда.
|
1. Сначала выбирают предпочтительную пару М-последовательностей a . и b дли- |
|||||||
ной |
N 2n 1 , выбрав характеристические полиномы |
f |
1 |
(x) |
и |
f |
2 |
(x) из таблиц [9,10]. |
|
|
|
|
|
|
|
||
2.Начальные условия для регистра 2 аналогичны начальным условиям для m- последовательности b , которые определяют характеристическую фазу согласно выражениям (7.24, а и б). Они определяются деление по формуле (7.18). При этом учитываются только первые n членов частного, которые определяют начальные условия сдвигового регистра 2..
3.Начальные условия для регистра 1 (последовательность a ) с соответствующим
характеристическим полиномом f1 (x) устанавливаются таким образом, чтобы в: крайней правой ячейке устанавливалась «единица», а начальные условия остальных ячеек регистра
– произвольны. Всего возможных комбинаций начальных условий регистра 1 будет 2n 1 . Рассмотрим пример получения сбалансированного кода Голда для 10-разрядного
регистра, имеющего период 1023. Выберем из таблиц [9,11] полиномы 1 и 5 (индекс де-
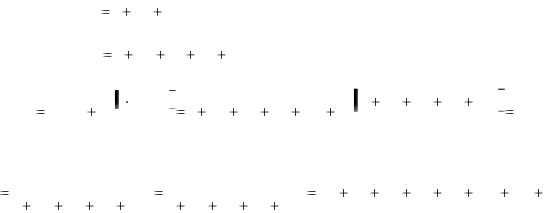
318
цимации q =5). Это полиномы 2011F и 2415Е. Эти два характеристических полинома
можно представить двоичными кодами с соответствующими полиномами:
10,000,001,001
1 2011F |
|
f1 (x) |
1 |
x3 |
x10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10,100,001,101 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 2415Е |
|
f 2 (x) |
1 |
x 2 |
x3 |
x8 |
|
x10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для четной степени полинома f 2 (x) |
получим |
|
|
|
|
|
|
||||||||||||||
g(x) f |
|
(x) |
d x f 2 (x) |
1 x |
2 |
x |
3 |
x |
8 |
x |
10 d x1 |
x3 |
x 4 |
x9 |
x11 |
x |
3 |
||||
2 |
|
dx |
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Характеристическая последовательность, генерируемая сдвиговым регистром 2, соответствующая полиному 2415Е, представима выражением
G(x) |
g(x) |
|
|
x3 |
|
x3 |
x5 |
x6 |
x7 |
x9 x10 x11 ... |
|
1 x 2 x3 x8 x10 |
1 x 2 |
x3 x8 |
x10 |
||||||||
|
|
|
|
|
|
||||||
Начальные условия характеристической фазы для сдвигового регистра 2 будут [1011101000]. Следовательно, в трѐх крайних правых ячейках сдвигового регистра 2 должны устанавливаться нулевые начальные условия. Таких сбалансированных последовательностей Голда для n =10 можно получить 512.
Использование несбалансированных последовательностей Голда ухудшает корреляционные и частотные характеристики генерируемого сигнала, что приводит к снижению вероятности доведения информации. Этим вопросам уделяется большое внимание в науч- но-тезнической литературе [10].
7.8.7.Устройства индикации цифровой аппаратуры
Для визуального определения состояния логических схем, счетчиков, распределителей н других узлов широко используется световая индикация. Она может производиться с
помощью миниатюрных ламп накаливания (например, НСМ-6,3-20), которые могут включаться на выход цифровых микросхем через эмиттерный повторитель. Пример включения
лампы накаливания на выход микросхемы 2ЛБ172 показан на рис. 7.32, а. В некоторых сериях имеются специальные схемы, предусматривающие подключение устройств индикации. Пример включения лампы накаливания на выход микросхемы 1ЛБ337 с открытым
коллектором показан на рнс. 7.32, б.
Индикация может осуществляться с помощью светодиодов, которые начинают светиться при подаче напряжения 3-5 В. Такие низкие напряжения позволяют легко согласовывать светодиоды с выходными сигналами цифровых микросхем.
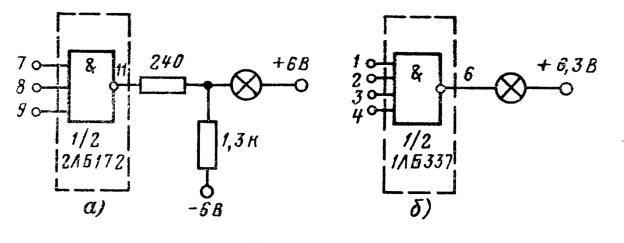
319
Рис. 7.32
Маломощные светодиоды можно включать вместо нагрузки инверторов микросхем. Более мощные светодиоды включаются через простейшие усилители, которые питаются от того же источника, что и сами микросхемы. Для считывания информации со счетчиков применяют цифросинтезирующие индикаторы на светодиодах. Они содержат набор светодиодов, зажигающихся в комбинациях, обеспечивающих высвечивание контуров цифр. Кроме того, устройства для индикации счетчиков широко используют газоразрядные цифровые индикаторные лампы (ИН-1, ИН-2, ИН-4, ИН-8, ИН-12), которые имеют один или два анода и десять катодов, выполненных в виде цифр от 0 до 9. При подаче на анод и соответствующий катод напряжения последний начинает светиться. Для управления цифровыми индикаторами требуется дешифратор и согласующее устройство по напряжению. (Оно необходимо, поскольку рабочее напряжение индикаторов около 200 В.)
7.9. Конструирование радиоэлектронных устройств на микросхемах
Рассмотрим теперь более подробно те элементы конструкции н процессы создания аппаратуры, которые являются специфичными, для микроэлектронных устройств, в частности многослойные печатные платы, а также вопросы компоновки узлов, субблоков, блоков, и обеспечения необходимого теплового режима.
Печатные платы служат основанием для монтажа микросхем и обеспечивают коммутацию всех элементов в соответствии с принципиальной схемой. Применение печатных плат позволяет на одиндва порядка повысить плотность компоновки по сравнению с объемным монтажом и на порядок снизить массу.
В устройствах малой сложности н в аппаратуре, к которой не предъявляются очень высокие требования к плотности монтажа применяются однослойные и двухслойные платы. В аппаратуре средней и большой сложности часто используются многослойные печатные платы.
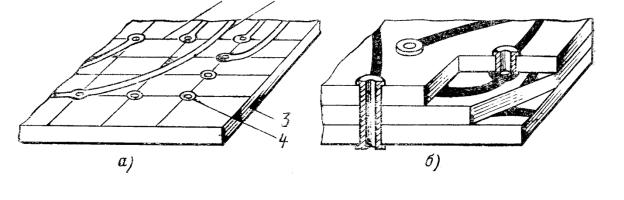
320
Однослойные и двухслойные платы (рис. 7.33, а) состоят иа основания, на которое с одной или двух сторон наносятся печатные проводники. Основания плат должны обладать достаточной механической прочностью, малыми диэлектрическими потерями, высокой нагревостойкостью и хорошей адгезией (сцепляемостью) материалов платы и печатных проводников. При изготовлении печатных плат широко используют стеклотекстолит, стеклоткань, керамику, фторопласт-4 и некоторые другие диэлектрики. Толщина плат
0,06—2 мм, а их габариты 70×110, 110×140, 110×170, 220×240 мм. Печатные проводники выполняются чаще всего из меди, алюминия, никеля или золота толщиной 35-70 мкм.
При выборе сечения, конфигурации и расстояния между проводниками исходят из допустимой плотности тока, рабочего напряжения, условий теплоотвода и прочности сцепления проводников, с основанием. Ширина проводников печатных плат обычно состав-
ляет 1,5-2,5 мм, а расстояние между ними 0,3-1 мм. Для плат с повышенной плотностью монтажа ширина проводников и зазоры между ними уменьшают до 0,25—0,4 мм. Во избежание короткого замыкания припоем во время пайки минимальное расстояние между проводниками у мест соединения берется равным 1,5 мм.
Рис. 7.33
Для установка микросхем и навесных деталей на плате просверливают и металлизируют отверстия, которые располагаются в углах координатной сетки (рис. 7.33, а). В большинстве случаев шаг сетки равен 2,5 мм, но иногда он может быть уменьшен до 0.5 мм. При шаге в 2,5 мм допуск на точность размещения отверстии составляет 0,13 мм, что сравнительно легко достигается с помощью современной технологии. Если сделать шаг меньше, точность размещения отверстий возрастает, но увеличивается стоимость плат. Например, при шаге 1,25 мм цена платы увеличивается вдвое.
Диаметр отверстия исходя из условий пайки должен быть больше диаметра вывода микросхемы на 0,15—0,25 мм и в 3 раза меньше толщины платы. Вокруг монтажного отверстия создается контактная площадка на 0,6—1,5 мм больше диаметра отверстия.
Конфигурация проводников выбирается такой, чтобы исключить отслаивания от основания, в частности не допускается образование прямых или острых углов, радиус за-


