Филлипов, решение ряда задач / 4. Однородные уравнения. / 113

№113

Для приведения уравнения к однородному определим точку пересечения прямых  и :

Вычтя из второго уравнения первое, получим . Подставив  во второе уравнение находим

Сделаем замену

Сделав подстановку в исходное уравнение, получим

Получили однородное уравнение. Делаем замену

Проверим, является ли решением . Подставляем это решение в исходное уравнение:

.

Последнее равенство не является тождеством. Следовательно  не является решением. Поделим обе части уравнения на , после раскрытия скобок и приведения подобных получим

Проверим, является ли  решением:

Подставляем найденное решение  в исходное уравнение:

0=0

Таким образом, получили тождество. Значит  является решением исходного уравнения

Проверим, является ли  решением уравнения.

Подставляем найденное решение  в исходное уравнение:

0=0

Таким образом, получили тождество. Значит  является решением исходного уравнения.

Делим обе части уравнения  на . Получаем

Для нахождения интеграла справа разложим дробь  на простые дроби методом неопределенных коэффициентов

Раскрыв скобки и приведя подобные получим

. Приравнивая коэффициенты при одинаковых степенях, получаем систему

Решив которую получим ,

Таким образом

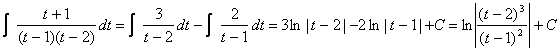
Таким образом получаем

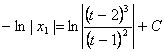
или

Попробуем из этого соотношения выразить  через . Подставим :

Переходя от  к  по формулам , получим

Отметим, что в ответ можно не включать найденное ранее решение , поскольку оно входит в серию решений  при .

Ответ: ,  _.