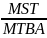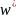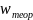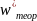3 лаба
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
Моделирование СМО с «нетерпеливыми» заявками
Отчет по лабораторной работе №3
по дисциплине «Моделирование автоматизированных информационных систем»
Вариант №4
Студент гр.:
_______
__.__.2024
Руководитель
преподаватель каф. КИБЭВС
_______ Е.А. Прозорова
__.__.2024
Томск 2024
Введение
Цель работы – Исследовать систему массового обслуживания (СМО) М/М/1 с нетерпеливыми заявками: построить имитационную модель системы и получить значения параметров ее функционирования. Проверить тождественность полных входного и выходного потоков в системе с ограничением очереди и «нетерпеливыми» заявками. Проверить основные теоретические формулы, в том числе преобразования Лапласса-Стилтьеса.
2 ХОД РАБОТЫ
Была собрана модель, соответствующая системе массового обслуживания (СМО) М/М/1 с ограниченным временем ожидания (с «нетерпеливыми» заявками) (рисунок 2.1).
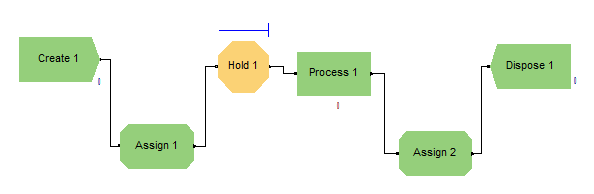
Рисунок 2.1 – Модель в программе
Была установлена длительность одного запуска (репликации) Trep и число запусков – Nrep в соответствии с вариантом 4: Количество повторений эксперимента с моделью равно 4, а длительность одного запуска (репликации) равно 60 часов (рисунок 2.2).
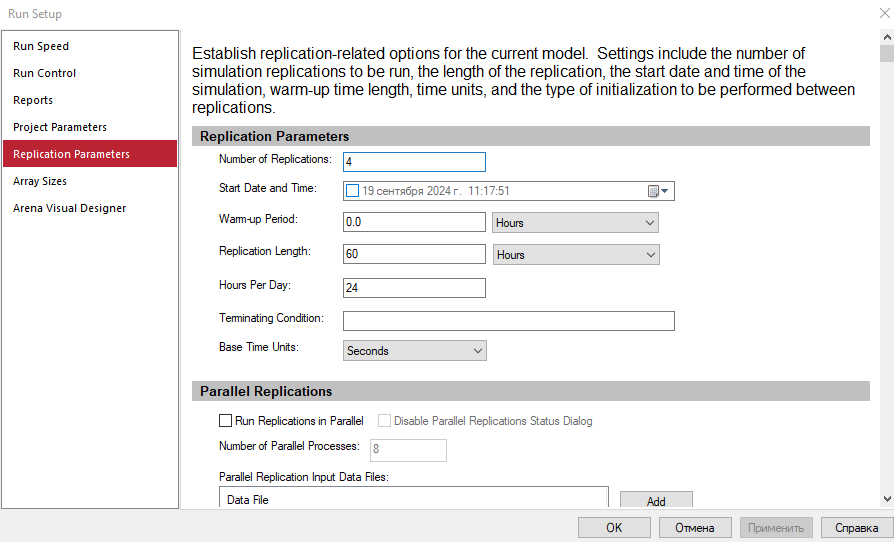
Рисунок 2.2 – Параметры репликации
Для блока Create в соответствии с вариантом было задано время между поступлениями заявок и время поступления первой заявки как экспоненциально распределенную случайную величину со средним значением равным MTBA (рисунок 2.3).
В блоке Process был создан ресурс, для которого время обслуживания заявки будет представлять собой экспоненциально распределенную случайную величину со средним значением MST (рисунок 2.4).
Блоке Assign было задано время ожидания для каждой заявки (в виде атрибута), как случайное число, распределенное экспоненциально со средним значением MWT, согласно варианту 4 (рисунок 2.5).

Рисунок 2.3 – Блок Create
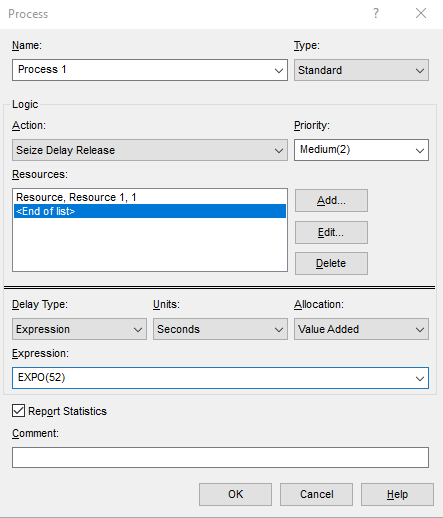
Рисунок 2.4 – Блок Process
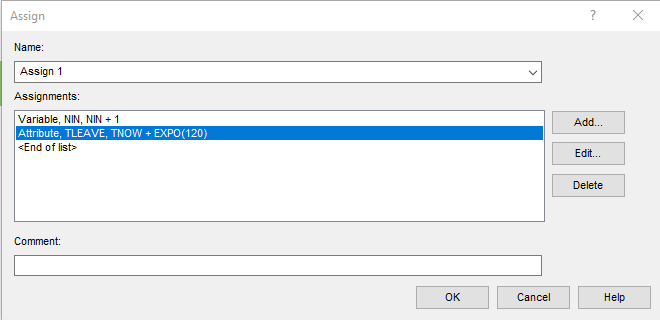
Рисунок 2.5 – Блок Assign
После чего было произведено моделирование работы СМО, с изменением значения MTBA в пределах 0.5-1.5 от заданного по варианту.
По завершению моделирования в таблицу 2.1 были внесены следующие показатели:
средний размер очереди;
среднее время ожидания в очереди;
среднее время пребывания заявки в системе;
процент заявок, не дождавшихся обслуживания.
Затем были построены графики зависимости указанных величин от интенсивности поступления заявок (рисунки 2.6 – 2.9)

Рисунок 2.6 – Зависимость среднего размера очереди от интенсивности поступления заявок
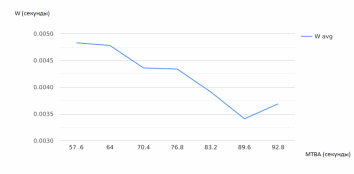
Рисунок 2.7 – Зависимость среднего времени ожидания в очереди от интенсивности поступления заявок
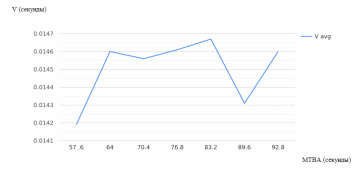
Рисунок 2.8 – Зависимость среднего времени пребывания заявки в очереди от интенсивности поступления заявок
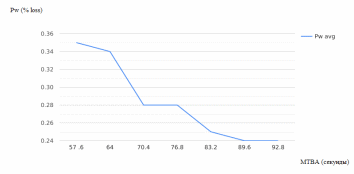
Рисунок 2.9 – Зависимость процента заявок, не дождавшихся обслуживания, от интенсивности поступления заявок
Таблица 2.1 – Моделирование с изменением MTBA
Nrep=3, Trep=60 |
MTBA, сек |
|
|
w, сек |
wтеор, сек |
v, сек |
vтеор, сек |
PW |
PW теор |
MST=52 MWT=120 |
57 .6 |
0.30266 |
0.3 |
0.00483 |
0.00457 |
0.01419 |
0.014 |
0.35 |
0.35 |
64 |
0.27014 |
0.27 |
0.00478 |
0.00457 |
0.01460 |
0.0145 |
0.34 |
0.34 |
|
70.4 |
0.22144 |
0.21444 |
0.00436 |
0.0042 |
0.01456 |
0.0145 |
0.28 |
0.28 |
|
76.8 |
0.20574 |
0.20546 |
0.00434 |
0.0042 |
0.01461 |
0.0146 |
0.28 |
0.28 |
|
83.2 |
0.16880 |
0.15674 |
0.00391 |
0.00385 |
0.01467 |
0.0146 |
0.25 |
0.25 |
|
89.6 |
0.13692 |
0.12759 |
0.00341 |
0.0032 |
0.01431 |
0.0125 |
0.24 |
0.24 |
Далее было проедено моделирование работы СМО, с изменением значения MST в пределах 0.5-1.5 от заданного по варианту. По завершению моделирования, полученные значения были добавлены в таблицу 2.2, а также построены графики зависимостей (рисунки 2.10 – 2.13).
Таблица 2.2 – Моделирование с изменением MST
Nrep=3, Trep=60 |
MTBA, сек |
|
|
w, сек |
wтеор, сек |
v, сек |
vтеор, сек |
PW |
PW теор |
MTBA=64 MWT=120 |
46.8 |
0.23122 |
0.22 |
0.00409 |
0.004 |
0.01319 |
0.013 |
0,248 |
0,25 |
52 |
0.27014 |
0.26759 |
0.00478 |
0.005 |
0.01460 |
0.014 |
0,335 |
0,34 |
|
55.64 |
0.28277 |
0.27859 |
0.005 |
0.005 |
0.01504 |
0.015 |
0,338 |
0,34 |
|
57.2 |
0.2985 |
0.285 |
0.00528 |
0.005 |
0.0156 |
0.1555 |
0,350 |
0,35 |
|
58.5 |
0.31652 |
0.3 |
0.0056 |
0.0056 |
0.01605 |
0.016 |
0,364 |
0,36 |
|
61.88 |
0.31598 |
0.31222 |
0.00559 |
0.00534 |
0.01621 |
0.016 |
0,368 |
0,37 |

Рисунок 2.10 – Зависимость среднего размера очереди от интенсивности поступления заявок
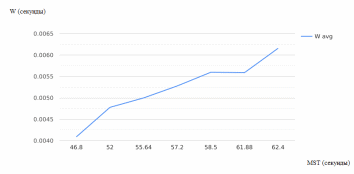
Рисунок 2.11 – Зависимость среднего времени ожидания в очереди от интенсивности поступления заявок

Рисунок 2.12 – Зависимость среднего времени пребывания заявки в очереди от интенсивности поступления заявок
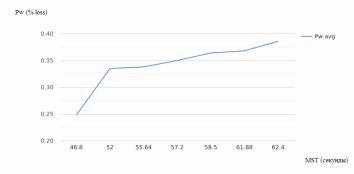
Рисунок 2.13 – Зависимость процента заявок, не дождавшихся обслуживания, от интенсивности поступления заявок
Далее было проведено моделирование работы СМО, с изменением значения MWT в пределах 0.5-1.5 от заданного по варианту. По завершению моделирования, полученные значения были добавлены в таблицу 2.2, а также построены графики зависимостей (рисунки 2.14 – 2.17).
Таблица 2.3 – Моделирование с изменением MWT
Nrep=3, Trep=60 |
MTBA, сек |
|
|
w, сек |
wтеор, сек |
v, сек |
vтеор, сек |
PW |
PW теор |
MTBA=64 MST=52 |
108 |
0.25555 |
0.25555 |
0.00456 |
0.0044 |
0.01433 |
0.015 |
0,338 |
0,34 |
120 |
0.27014 |
0.27 |
0.00478 |
0.0045 |
0.0146 |
0.0145 |
0,335 |
0,34 |
|
132 |
0.27109 |
0.27 |
0.0048 |
0.0047 |
0.01477 |
0.014685 |
0,34 |
0,34 |
|
144 |
0.28008 |
0.27569 |
0.00495 |
0.0049 |
0.01476 |
0.146 |
0,33 |
0,33 |
|
156 |
0.27816 |
0.2685 |
0.00499 |
0.0049 |
0.01487 |
0.01485 |
0,32 |
0,32 |
|
168 |
0.2942 |
0.29567 |
0.00522 |
0.005 |
0.01506 |
0.15 |
0,328 |
0,33 |
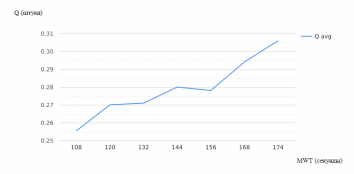
Рисунок 2.14 – Зависимость среднего размера очереди от интенсивности поступления заявок
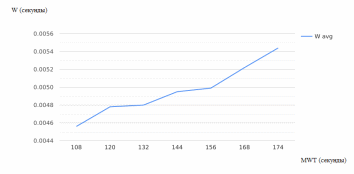
Рисунок 2.15 – Зависимость среднего времени ожидания в очереди от интенсивности поступления заявок
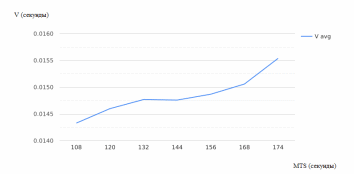
Рисунок 2.16 – Зависимость среднего времени пребывания заявки в очереди от интенсивности поступления заявок
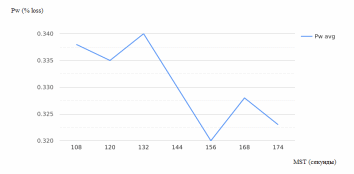
Рисунок 2.17 – Зависимость процента заявок, не дождавшихся обслуживания, от интенсивности поступления заявок
На основании проделанных моделирований и полученных значений можно сделать выводы:
Для эффективного функционирования СМО необходимо тщательно подбирать значения MTBA и MST, чтобы поддерживать оптимальное соотношение ρ. Ведь если соотношение ρ = MST / MTBA близко к 1, это указывает на высокую нагрузку на систему, что приводит к увеличению времени ожидания;
Оптимизация MWT требует балансировки между MTBA и MST для достижения желаемого уровня обслуживания.
Далее была проверена справедливость следствия из формулы Литтла, результаты проверки занесены в таблицу 2.4. Смысл формулы Литтла заключается в том, что она позволяет понять, как различные параметры системы взаимодействуют друг с другом:
Увеличение количества заявок при фиксированной интенсивности входящего потока приведёт к увеличению времени ожидания;
Это также указывает на то, что для поддержания эффективной работы системы необходимо оптимальное управление количеством задач в процессе.
Таким образом, формула помогает менеджерам и специалистам по оптимизации процессов предсказывать и управлять поведением систем, обеспечивая более высокую эффективность и предсказуемость.
Таблица 2.4 – Проверка формулы Литтла
№ п/п |
|
w, сек |
v, сек |
PW’ |
PW |
1 |
64 |
0,00457 |
0,0145 |
0,364 |
0,35 |
2 |
89,6 |
0,0032 |
0,0125 |
0,167 |
0,24 |
3 |
64 |
0,00409 |
0,01319 |
0,418 |
0,25 |
4 |
57,6 |
0,00457 |
0,014 |
0,457 |
0,35 |
5 |
76,8 |
0,0042 |
0,0146 |
0,201 |
0,28 |
6 |
64 |
0,00559 |
0,01621 |
0,32 |
0,368 |
7 |
64 |
0,005 |
0,0149 |
0,368 |
0,32 |
8 |
83,2 |
0,00391 |
0,01467 |
0,105 |
0,25 |
Затем в модель системы M/M/1/r был добавлен поток «терпеливых» контрольных заявок, которые занимают место в очереди и ожидают обслуживания, но дождавшись не занимают сервер, а покидают систему. Время между поступлением «терпеливых» заявок было задано экспоненциально распределенным в соответствии с таблицей 2.5.
Значения MTBA, MST, MWT были заданы согласно варианту. Среднее время ожидания в очереди для «терпеливых» заявок было определено, а результаты эксперимента были сведены в таблицу 2.5
После заполнения таблицы были построены графики (рисунки 2.18 – 2.25) зависимостей среднего времени ожидания в очереди (для нетерпеливых заявок), среднего времени ожидания в очереди (для терпеливых заявок) от
• MST (при постоянных MWT, MTBA);
• MTBA (при постоянных MWT, MST);
• MWT (при постоянных MTBA, MST);
• MST/MTBA (при постоянном MWT).
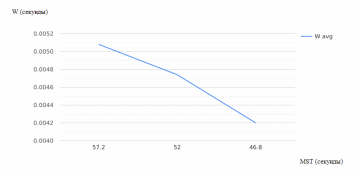
Рисунок 2.18 – Зависимость среднего времени ожидания в очереди (для нетерпеливых заявок) от MST
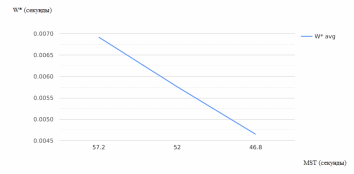
Рисунок 2.19 – Зависимость среднего времени ожидания в очереди (для терпеливых заявок) от MST

Рисунок 2.20 – Зависимость среднего времени ожидания в очереди (для нетерпеливых заявок) от MTBA
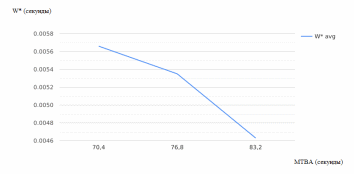
Рисунок 2.21 – Зависимость среднего времени ожидания в очереди (для терпеливых заявок) от MTBA
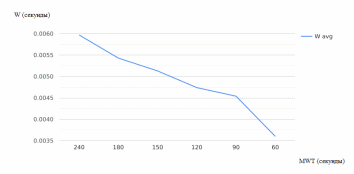
Рисунок 2.22 – Зависимость среднего времени ожидания в очереди (для нетерпеливых заявок) от MWT
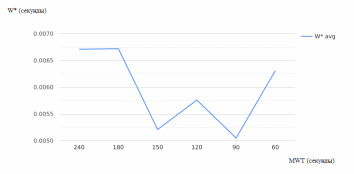
Рисунок 2.23 – Зависимость среднего времени ожидания в очереди (для терпеливых заявок) от MWT

Рисунок 2.24 – Зависимость среднего времени ожидания в очереди (для нетерпеливых заявок) от MST/MTBA

Рисунок 2.25 – Зависимость среднего времени ожидания в очереди (для терпеливых заявок) от MST/MTBA
На основании результатов эксперимента можно сделать выводы:
Увеличение среднего времени между прибытием заявок (MTBA) приведет к уменьшению средней загрузки системы, что снизит среднее время ожидания в очереди для обеих категорий заявок;
Для нетерпеливых заявок это может привести к меньшему количеству отказов из-за превышения времени ожидания;
Снижение MTBA создаст более высокую нагрузку на систему, что увеличит среднее время ожидания как для нетерпеливых, так и для терпеливых заявок;
Увеличение среднего времени ожидания (MWT) в системе может привести к увеличению общего времени ожидания в очереди для нетерпеливых заявок, так как они могут покидать систему раньше;
Для терпеливых заявок увеличение MWT может не оказать значительного влияния на их среднее время ожидания, так как они готовы ждать дольше;
Если отношение среднего времени обслуживания к среднему времени между прибытием заявок увеличивается, это может указывать на то, что система становится менее эффективной. В результате среднее время ожидания в очереди будет расти для обеих категорий заявок. Снижение этого отношения может указывать на более эффективное использование ресурсов системы, что приведет к уменьшению среднего времени ожидания в очереди.
Далее была собрана модель, соответствующую СМО М/М/1/r с ограниченным временем ожидания (рисунок 2.26).
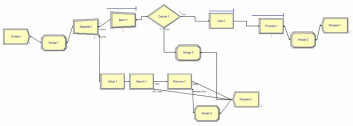
Рисунок 2.26 – СМО М/М/1/r с ограниченным временем ожидания
Затем была проведена серия экспериментов с изменением размера очереди, по завершению которой в таблицу 2.6 были занесены следующие показатели:
процент заявок, потерянных из-за заполнения очереди;
процент заявок, не дождавшихся обслуживания;
На основании полученных показателей были построены графики зависимости этих показателей от размера очереди (рисунки 2.27 – 2.28).
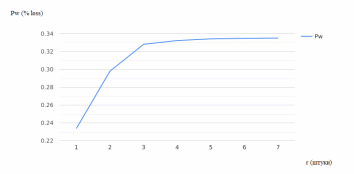
Рисунок 2.27 – Зависимость процента заявок, потерянных из-за заполнения очереди, от размера очереди
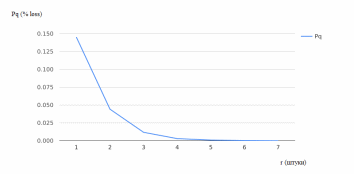
Рисунок 2.28 – Зависимость процента заявок, не дождавшихся обслуживания, от размера очереди
Затем была проведена серия экспериментов с изменением времени «терпения» заявок от 0.5 до 1.5 MWT, по завершению которой в таблицу 2.7 были занесены следующие показатели:
процент заявок, потерянных из-за заполнения очереди;
процент заявок, не дождавшихся обслуживания;
На основании полученных показателей были построены графики зависимости этих показателей от размера очереди (рисунки 2.29 – 2.30).
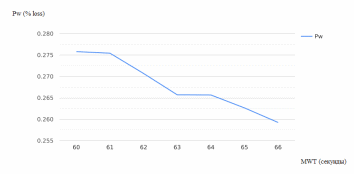
Рисунок 2.29 – Зависимость процента заявок, потерянных из-за заполнения очереди, от размера очереди
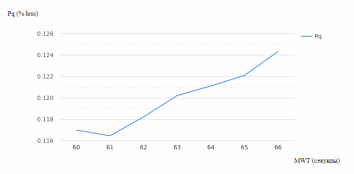
Рисунок 2.30 – Зависимость процента заявок, не дождавшихся обслуживания, от размера очереди
Затем были построены гистограммы (рисунки 2.31 – 2.33) для времени между заявками, покидающими систему по причинам:
а) по причине успешного завершения обслуживания;
б) по причине отсутствия мест в очереди;
в) по причине истечения времени ожидания.
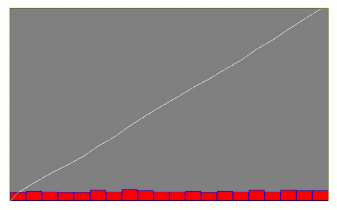
Рисунок 2.31 – Успешное завершение обслуживания
Рисунок 2.32 – Отсутствие мест в очереди

Рисунок 2.33 – Истечение времени обслуживания
На рисунках 2.34 – 2.35 представлены графики интенсивности входного и входного потока заявок.
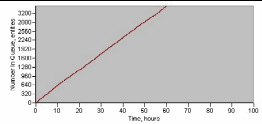
Рисунок 2.34 – Интенсивность входного потока заявок
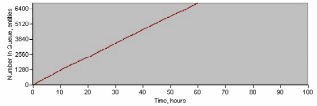
Рисунок 2.35 – Интенсивность выходного потока заявок
После были сделаны выводы о влиянии параметров распределений поступления заявок, обслуживания и времени ожидания на параметры функционирования СМО:
средняя длина очереди: Увеличение интенсивности поступления заявок при фиксированной интенсивности обслуживания приводит к увеличению средней длины очереди. Это также связано с вероятностью отказа в обслуживании, которая возрастает при высокой загруженности системы;
время ожидания: Как показано в исследованиях, параметры распределений напрямую влияют на среднее время ожидания. Например, увеличение коэффициента вариации времени обслуживания (например, переход от экспоненциального к гиперэкспоненциальному распределению) может значительно увеличить среднее время ожидания;
вероятность отказа: При высокой загрузке системы вероятность отказа (когда все каналы заняты и очередь заполнена) становится критически важной. Это можно оценить через формулы для вероятности отказа в зависимости от числа каналов и интенсивностей потоков.
Таблица 2.5 – Вторая часть задания
Для обеспечения лучшей точности увеличено время моделирования: 3·Trep = …, Nrep = 5. |
|||||||||
MTBA |
MST |
MWT |
|
1024 |
256 |
Теоретические значения (без учёта MTBC) |
|||
|
|
|
|
|
|
||||
64 |
57,2 |
120 |
0,89375 |
0.00508 |
0.00692 |
0.00593 |
0.0065 |
0.0055 |
0.006758 |
52 |
0,8125 |
0.00474 |
0.00576 |
0.00533 |
0.00631 |
0.0051 |
0.006 |
||
46,8 |
0,73125 |
0.0042 |
0.00465 |
0.00417 |
0.00464 |
0.0041 |
0.0046 |
||
70,4 |
52 |
0,738636364 |
0.00458 |
0.00566 |
0.00507 |
0.00597 |
0.00475 |
0.0054769 |
|
76,8 |
0,677083333 |
0.00441 |
0.00535 |
0.00439 |
0.00531 |
0.00485 |
0.0052 |
||
83,2 |
0,625 |
0.00383 |
0.00463 |
0.00476 |
0.0058 |
0.00425 |
0.0044 |
||
64 |
240 |
0,8125 |
0.00597 |
0.00671 |
0.00643 |
0.00668 |
0.00623 |
0.0064965 |
|
180 |
0,8125 |
0.00543 |
0.00672 |
0.0056 |
0.00599 |
0.005764 |
0.006 |
||
150 |
0,8125 |
0.00513 |
0.00521 |
0.00517 |
0.00607 |
0.005567 |
0.00556 |
||
120 |
0,8125 |
0.00474 |
0.00576 |
0.00533 |
0.00631 |
0.005 |
0.006167 |
||
90 |
0,8125 |
0.00454 |
0.00505 |
0.00458 |
0.00558 |
0.005123 |
0.00524 |
||
60 |
0,8125 |
0.0036 |
0.00631 |
0.00404 |
0.00593 |
0.003865 |
0.006 |
||

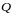
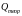
 ,
сек-1
,
сек-1