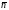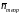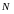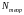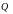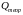2 лаба

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

Моделирование СМО М/М/n/r

Отчет по лабораторной работе №2

по дисциплине «Моделирование автоматизированных информационных систем»

Вариант №4

Студент гр. :

_______

__.__.2024

Руководитель

преподаватель каф. КИБЭВС

_______ Е.А. Прозорова

__.__.2024

Томск 2024

Введение

Цель работы - Исследовать систему массового обслуживания (СМО) М/М/r/n: построить имитационную модель системы и получить значения параметров ее функционирования. Проверить основные теоретические формулы. Исследовать способы повышения пропускной способности системы и последствия их применения.

2 ХОД РАБОТЫ

Была собрана модель, соответствующая системе массового обслуживания (СМО) М/М/n/r (рисунок 2.1).

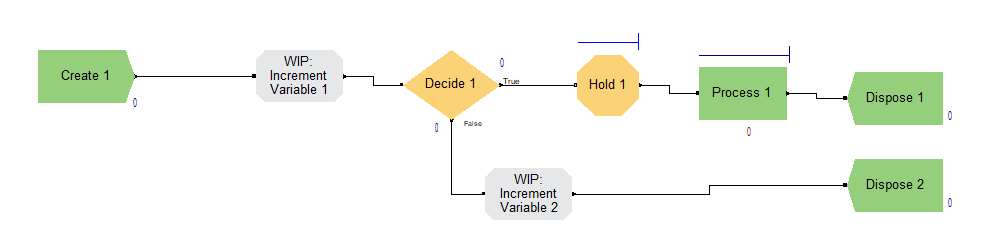
Рисунок 2.1 – Модель в программе

Была установлена длительность одного запуска (репликации) T_rep и число запусков – N_rep в соответствии с вариантом 4: Количество повторений эксперимента с моделью равно 3, а длительность одного запуска (репликации) равно 50 (рисунок 2.2).

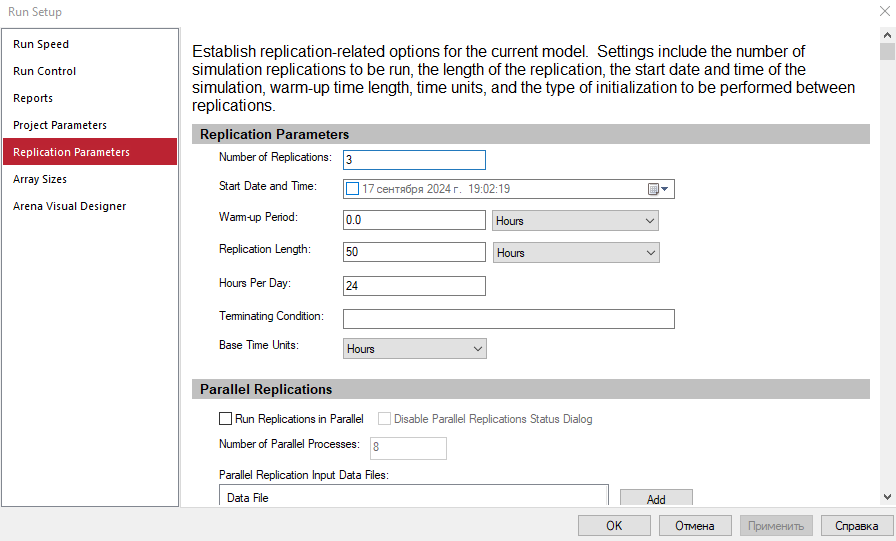
Рисунок 2.2 – Параметры репликации

Для блока Create в соответствии с вариантом было задано время между поступлениями заявок и время поступления первой заявки как экспоненциально распределенную случайную величину со средним значением равным MTBA (рисунок 2.3).

В блоке Process был создан ресурс, для которого время обслуживания заявки будет представлять собой экспоненциально распределенную случайную величину со средним значением MST, чтобы величина ρ была равна 0.8 (рисунок 2.4).

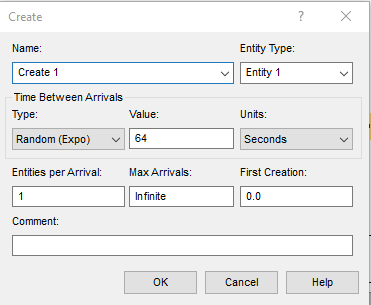
Рисунок 2.3 – Блок Create

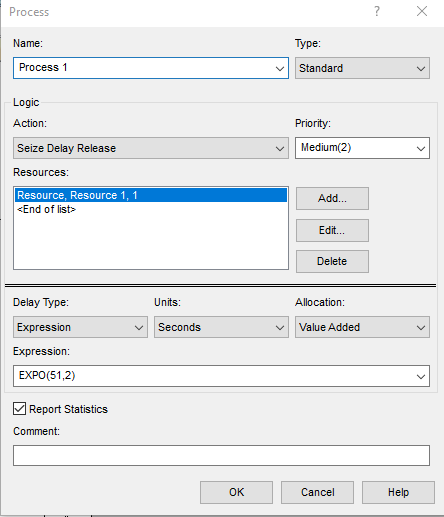
Рисунок 2.4 – Блок Process

По завершению этапа моделирования в таблицу 2.1 были внесены следующие показатели:

• среднее время ожидания в очереди;

• процент потерянных заявок;

• среднюю загрузку ресурса (сервера).

ρ – Параметр нагрузки на систему;

r – Размер очереди в блоке Hold 1;

w – Среднее время ожидания обслуживания;

w_avg – Среднее время ожидания обслуживания (теоритическое);

w_max – Среднее время обслуживания (максимальное);

 – Вероятность потери заявки (доля потерянных заявок);

_теор – Вероятность потери заявки (доля потерянных заявок) (теоритическая);

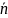– Среднее число занятых серверов;

_теор – Среднее число занятых серверов (теоритическое).

Таблица 2.1 – Первая часть задания

Nrep=3, Trep=50	r	w, сек	Wavg, сек	wmax, сек		теор
ρ=0.8	0	0	0	0	1	1	0	0
	1	0.00592759	0.00657	0.09473	0.288342	0.26846342	0.59926	0.21477074
	3	0.01631358	0.01822	0.12921	0.135063	0.1260063	0.71377	0.10080504
	5	0,02400515	0.02680	0.17308	0.065323	0.06055303	0.76169	0.04844242
	7	0.03193135	0.03536	0.23354	0.04184	0.03675184	0.78706	0.02940147
	10	0.03845814	0.04228	0.28109	0.02647	0.02345117	0.80462	0.01876094

Ниже представлены графики зависимостей рассмотренных показателей от величины r (рисунки 2.5 – 2.7).

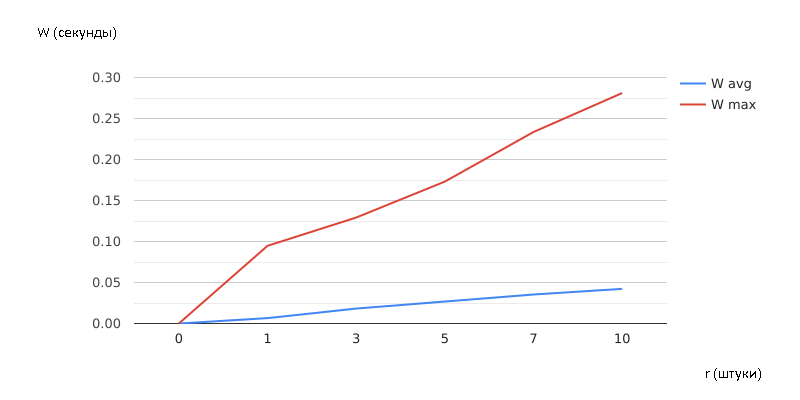
Рисунок 2.5 – Зависимость w и w_max от MTBA

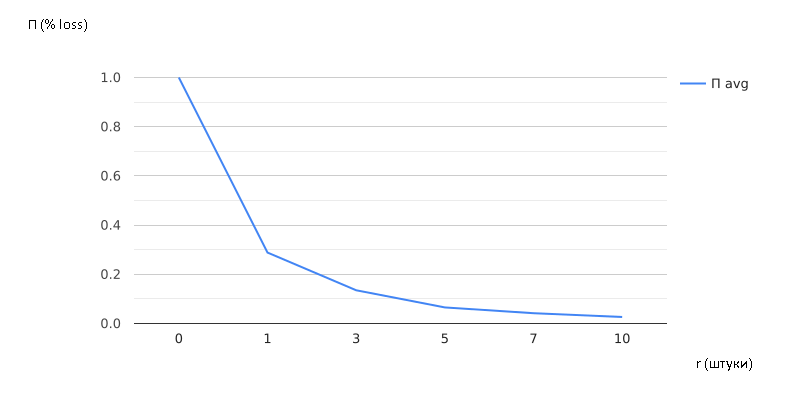
Рисунок 2.6 – Зависимость от r

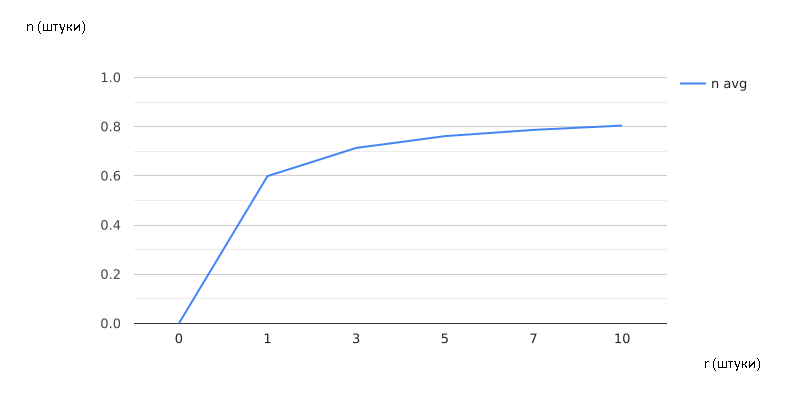
Рисунок 2.7 – Зависимость от r

Для ρ=0.8 и заданного времени моделирования было подобрано значение r равное 15, при нем исследуемая система будет идентична системе M/M/1 (доля потерянных заявок будет меньше 0.5%).

Затем на основании одной репликации для ρ=0.8 и произвольного ограничения размера очереди (3 ≤ r ≤ 5):

• был построен график зависимости для доли потерянных заявок от времени (рисунок 2.8);

• среднее время между отработанными заявками, уходящими из системы = 0.03386 (сек);

• среднее время между потерянными заявками = 0.0129 (сек);

• среднее время между заявками, уходящими из системы (отработанными и потерянными) = 0.02309 (сек).

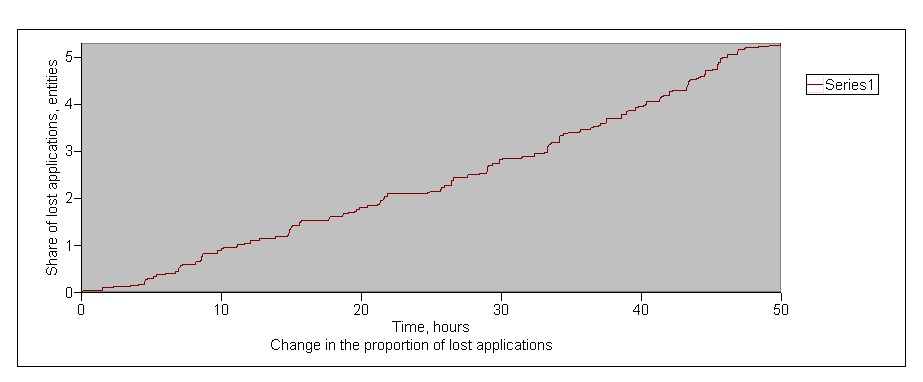
Рисунок 2.8 – Зависимость доли потерянных заявок от времени

Далее была собрана модель, соответствующая системе массового обслуживания (СМО) М/М/2/0 с равномерной загрузкой серверов (рисунок 2.9).

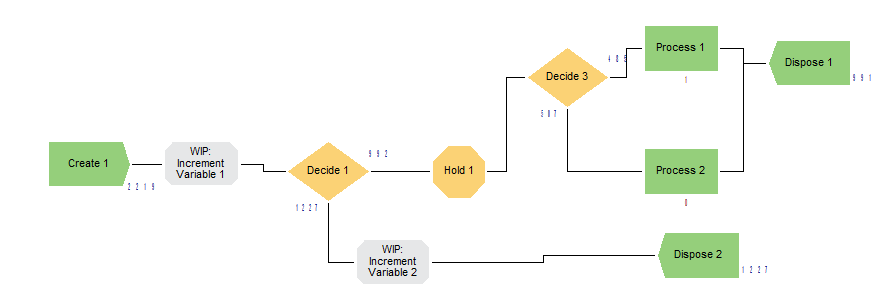
Рисунок 2.9 – Модель М/М/2/0

Была установлена длительность одного запуска (репликации) T_rep и число запусков – N_rep в соответствии с вариантом 4: Количество повторений эксперимента с моделью равно 3, а длительность одного запуска (репликации) равно 50 (рисунок 2.10).

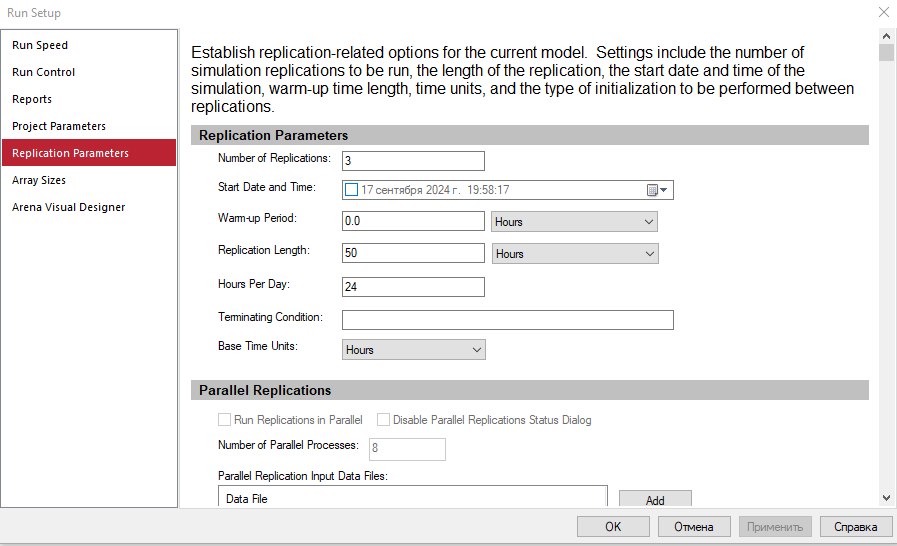
Рисунок 2.10 – Параметры репликации

Для блока Create в соответствии с вариантом было задано время между поступлениями заявок и время поступления первой заявки как экспоненциально распределенную случайную величину со средним значением равным MTBA (рисунок 2.11).

В блоке Process был создан ресурс, для которого время обслуживания заявки будет представлять собой экспоненциально распределенную случайную величину с таким средним значением MST, чтобы величина ρ была равна 0.75 (рисунок 2.12).

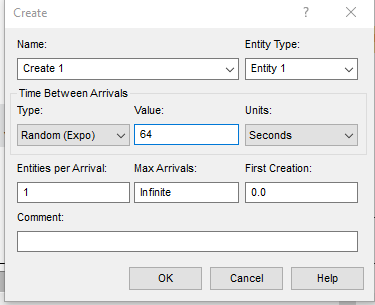
Рисунок 2.11 – Блок Create

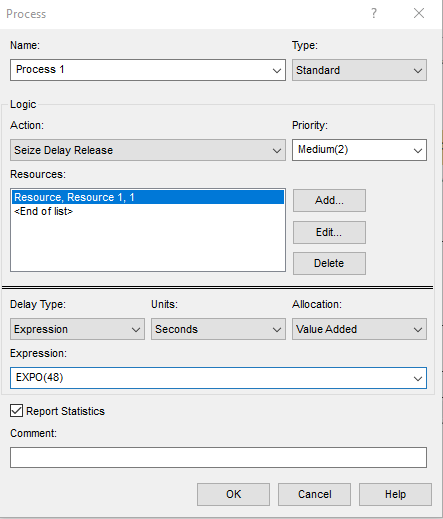
Рисунок 2.12 – Блок Process

По завершению моделирования были сведены в таблицу 2.2 следующие показатели:

a. средний размер очереди;

b. среднее количество заявок в системе;

c. среднее время пребывания заявки в системе;

d. среднее время ожидания в очереди;

e. процент потерянных заявок;

f. средняя загрузка ресурсов (серверов).

Затем было повторено моделирование, с применением среднего значения времени такого, что величина ρ принимала значения: 1, 1.5, 1.95. После чего были построены графики зависимостей для показателей a, d, e, f от величины ρ (рисунки 2.13 – 2.16).

Затем для системы M/M/2 были определены стационарные вероятности присутствия в системе k заявок (k =1,2, ..,7). Величина MTBA была взята равной 50 секунд. Величины Nrep, Trep и MST были определены в соответствие с таблицей 3 из методического пособия. Результаты сведены в таблицу 2.3.

Таблица 2.3 – Стационарные вероятности

	Теоретическое значение	По числу наблюдений		По доле времени
		Число наблюдений	Вероятность	Доля времени	Вероятность
p0=	0.173	362	0.1678	16.777	0.16777
p1=	0.42	617	0.4198	41.980	0.4198
p2=	0.18	394	0.182	18.201	0.18201
p3=	0.0922	217	0.0966	9.6634	0.096634
p4=	0.0555	111	0.0556	5.5561	0.055561
p5=	0.03	53	0.03	3.0037	0.030037
p6=	0.0185	33	0.0184	1.8383	0.018383
p7=	0.0112	22	0.0106	1.0640	0.01064
p>7=	0.0196	8	0.0191	1.9147	0.019147
Всего	1	1817	0.9999	99.9982	0.999982

Различие между результатами связано с тем, что:

• системы могут иметь различные конфигурации (например, M/M/1, M/M/2 и т.д.), что влияет на результаты. В системах с различным количеством каналов обслуживания результаты будут различаться из-за изменения коэффициента загрузки;

• если интенсивность поступления заявок (λ) или интенсивность обслуживания (μ) изменяются, это напрямую влияет на стационарные вероятности. Например, увеличение λ может привести к более высокой загрузке системы и, следовательно, к изменению вероятностей;

• стационарные вероятности являются теоретическими значениями, основанными на предположениях о бесконечном числе заявок и бесконечном времени наблюдения. В реальных системах могут возникать статистические колебания из-за конечного числа наблюдений или временных интервалов.

Таблица 2.2 – Вторая часть задания

Nrep=3, Trep=50	ρ					w, сек	wтеор, сек	v, сек	vтеор, сек		теор
MTBA=64	0.75	0.67193	0.625	0.12332	0.12	0.00602	0.00268111	0.01177	0,011899465	0.31561	0.28131561	0.27479	0.53901329
	1	0.81507	0.8	0.17728	0.155	0.00947	0.00414349	0.01480	0,013215591875	0.383162	0.33148212	0.31614	0.6685178
	1.5	1.2188	1.2	0.38093	0.3765	0.02426	0.01076016	0.02166	0,019714055	0.5084559	0.44684559	0.40553	0.82973682
	1.95	1.9894	1.825	0.98422	0.9625	0.06695	0.03065822	0.03515	0,0223977418	0.598311	0.49839113	0.52122	0.9781373

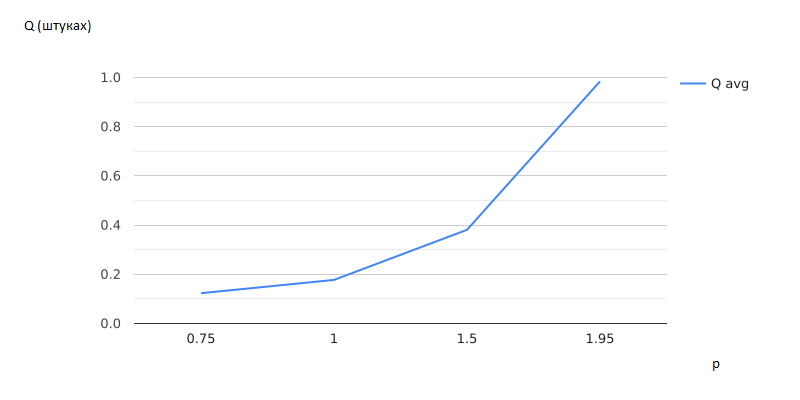
Рисунок 2.13 – Зависимость среднего размера очереди от ее размера

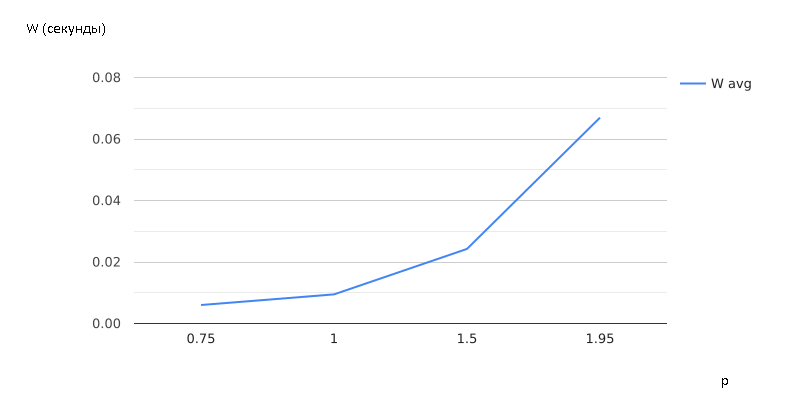
Рисунок 2.14 – Зависимость среднего времени ожидания очереди от размера очереди

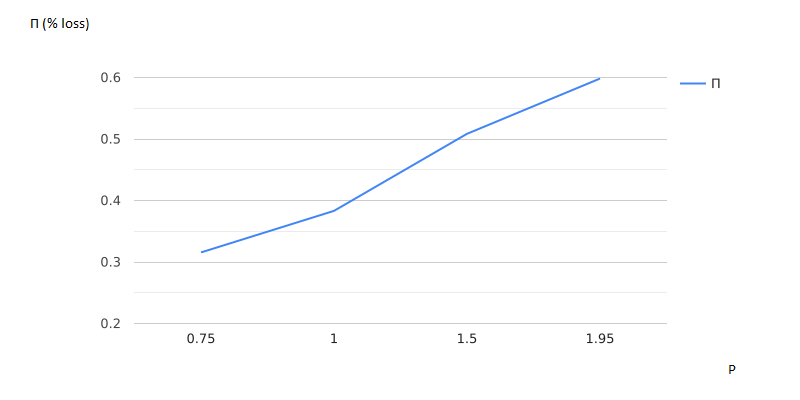
Рисунок 2.15 – Зависимость процента потерянных заявок от размера очереди

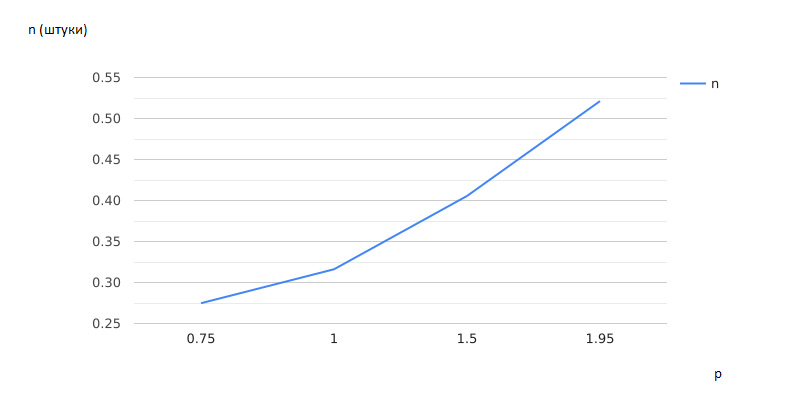
Рисунок 2.16 – Зависимость средней загрузки ресурсов (сервера) от размера очереди

Заключение

В ходе лабораторной работы были исследована система массового обслуживания (СМО) М/М/n/r: построена имитационная модель системы и получены значения параметров её функционирования, а также проверены основные теоретические формулы.

Отчет составлен согласно ОС ТУСУР 2021.