
1 лаба
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
Моделирование СМО М/М/1
Отчет по лабораторной работе №1
по дисциплине «Моделирование автоматизированных информационных систем»
Вариант №4
Студент гр. :
_______
__.__.2024
Руководитель
преподаватель каф. КИБЭВС
_______ Е.А. Прозорова
__.__.2024
Томск 2024
Введение
Цель работы – Исследовать систему массового обслуживания (СМО) М/М/1: построить имитационную модель системы и получить значения параметров её функционирования. Проверить основные теоретические формулы.
2 Ход работы
Собираем модель, соответствующую системе массового обслуживания (СМО) М/М/1 (рисунок 2.1). И заполняем таблицу 2.1 по данным из отчёта программы.

Рисунок 2.1 – Модель в программе
Таблица 2.1 – Первая часть задания
Nrep=…, Trep=… |
MST, сек |
|
|
|
|
|
|
w, сек |
wтеор, сек |
wmax, сек |
v, сек |
vтеор, сек |
vmax, сек |
|
|
MTBA=64 |
32 |
1,5143000
|
1 |
15 |
0,91807
|
0,5 |
14 |
0,01621
|
0,015625
|
0,19261
|
0,02674
|
0,03125
|
0,19864
|
0,59628
|
0,5
|
38,4 |
1,4927000
|
1,5 |
14 |
0,88302
|
0,9
|
13 |
0,01541
|
0,0140625
|
0,21287
|
0,02605
|
0,0390625
|
0,21874
|
0,60976
|
0.6
|
|
48 |
3,6650000
|
3
|
37 |
2,8966000
|
2,2500000
|
36 |
0,05055
|
0,046875
|
0,54135
|
0,06398
|
0,0625
|
0,5512
|
0,76839
|
0,75
|
|
57,6 |
12,613
|
9 |
51 |
11,701
|
8,1
|
50 |
0,20430
|
0,140625
|
0,89868
|
0,22027
|
0,15625
|
0,90574
|
0,91277
|
0,9
|
|
64 |
26,537
|
98,01
|
84
|
27,493
|
99 |
85 |
0,4618
|
1,546875
|
1,6249
|
0,47893
|
1,5625
|
1,6468
|
0,95621
|
0,99
|
Ниже представлены графики для N, Q, W, V (рисунок 2.2-2.5). А также таблица 2.2 с новыми значениями показателей.

Рисунок 2.2 – Зависимость N и N max от MTBA

Рисунок 2.3 – Зависимость Q и Q max от MTBA
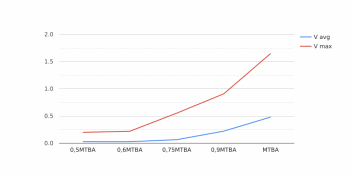
Рисунок 2.4 – Зависимость V и V max от MTBA

Рисунок 2.5 – Зависимость W и W max от MTBA
Nrep=…, Trep=… |
MTBA, сек |
|
|
|
|
|
|
w, сек |
wтеор, сек |
wmax, сек |
v, сек |
vтеор, сек |
vmax, сек |
|
|
MST=76 |
76 |
42,226
|
99 |
133 |
41,238
|
98
|
132
|
0,87024
|
1,3026316
|
2,6071
|
0,89122
|
1,3157895
|
2,6164
|
0,9878
|
0,99
|
83,6 |
6,4463
|
9,989011
|
41 |
5,6325
|
9,080011
|
40 |
0,13107
|
0,1314344
|
0,7768
|
0,15133
|
0,1445922
|
0,78384
|
0,81381
|
0,909
|
|
95 |
3,6685
|
4 |
17 |
2,8804
|
3,2
|
16 |
0,07595
|
0,0526316
|
0,37053
|
0,09676
|
0,0657895
|
0,39813
|
0,78803
|
0,8 |
|
114 |
2,0188
|
2 |
11 |
1,3369
|
1,3333333
|
10 |
0,03909
|
0,0263158
|
0,24696
|
0,0591
|
0,0394737
|
0,27571
|
0,68193
|
0,6666667
|
|
152 |
1,0273
|
1 |
8 |
0,48751
|
0,5 |
7 |
0,01942
|
0,0131579
|
0,16816
|
0,04093
|
0,0263158
|
0,21538
|
0,53981
|
0,5 |
Таблица 2.2 – Вторая часть задания
Ниже представлены графики для N, Q, W, V (рисунок 2.6-2.9).

Рисунок 2.6 – Зависимость N и N max от MTBA
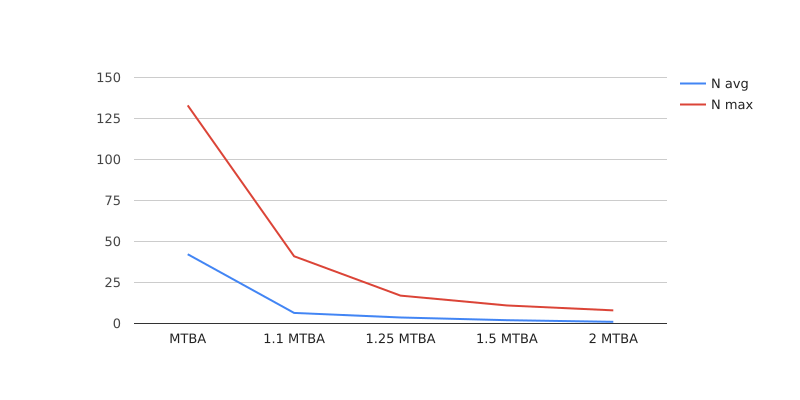
Рисунок 2.7 – Зависимость Q и Q max от MTBA

Рисунок 2.8 – Зависимость V и V max от MTBA

Рисунок 2.9 – Зависимость W и W max от MTBA
Ниже представлена проверка формул Литтла в таблицах 2.3 и 2.4.
Таблица 2.3 – Таблица проверки v
№ опыта |
N |
v, сек |
λ |
λтеор |
1 |
1 |
0.02674 |
0.01602 |
1/64 |
2 |
1,5 |
0.02605 |
0.01649 |
1/64 |
3 |
3 |
0.06398 |
0.04232 |
1/64 |
4 |
9 |
0.22027 |
0.13266 |
1/64 |
5 |
99 |
0.47893 |
0.15988 |
1/64 |
6 |
100 |
0,8912200 |
0,0161 |
1/76 |
7 |
12,0879121 |
0,1513300 |
0.13061 |
1/83,6 |
8 |
6,25 |
0,0967600 |
0.07251 |
1/95 |
9 |
4,5 |
0,0591000 |
0.02923 |
1/114 |
10 |
4 |
0,0409300 |
0.0182 |
1/152 |
Таблица 2.4 – Таблица проверки w
№ опыта |
Q |
w, сек |
λ |
λтеор |
1 |
0,5 |
0.01621 |
0.01602 |
1/64 |
2 |
0,54 |
0.01541 |
0.01649 |
1/64 |
3 |
2,25 |
0.05055 |
0.04232 |
1/64 |
4 |
8,1 |
0.20430 |
0.13266 |
1/64 |
5 |
98.01 |
0,4618000 |
0.15988 |
1/64 |
6 |
99 |
0.87024 |
0,0161 |
1/76 |
7 |
10,9879121 |
0,1310700 |
0.13061 |
1/83,6 |
8 |
5 |
0,0759500 |
0.07251 |
1/95 |
9 |
3 |
0,0390900 |
0.02923 |
1/114 |
10 |
2 |
0,0194200 |
0.0182 |
1/152 |
На основании выполненной работы можно сделать выводы:
увеличение интенсивности потока заявок может привести к перегрузке системы, если она не способна адаптироваться к возросшему количеству входящих заявок. Это может вызвать увеличение времени ожидания и число необслуженных заявок;
разные законы распределения (например, экспоненциальное, нормальное) влияют на среднее время обслуживания и, соответственно, на общую пропускную способность системы. Экспоненциальное распределение, часто используемое в моделировании, предполагает, что время обслуживания не зависит от предыдущих заявок, что может быть не всегда реалистично;
если интенсивность обслуживания ниже, чем интенсивность поступления заявок, это приводит к накоплению очередей. Эффективное управление параметрами обслуживания (например, увеличение числа каналов) может улучшить устойчивость системы и снизить время ожидания.
Ниже представлены графики изменения размера очереди и среднего времени ожидания (по одной репликации) (рисунки 2.10 – 2.11).

Рисунок 2.10 – График изменения размера очереди
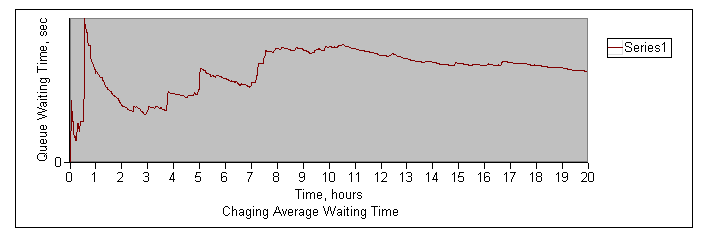
Рисунок 2.11 – График изменения среднего времени ожидания
Заключение
В ходе лабораторной работы были исследована система массового обслуживания (СМО) М/М/1: построена имитационная модель системы и получены значения параметров её функционирования, а также проверены основные теоретические формулы.
Отчет составлен согласно ОС ТУСУР 2021.








