3.2 Метод Рунге-Кутта 2-го порядка
Данный метод точнее, чем метод Эйлера, но для его применения нужно, чтобы была возможность увеличения числа узлов (рисунок 3.4).
Рисунок 3.4 – Формула метода Рунге-Кутта 2-го порядка
Реализация метода Рунге-Кутта 2-го порядка на языке программирования C# изображена на рисунке 3.5.
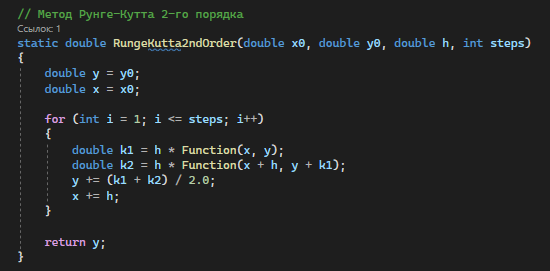
Рисунок 3.5 – Код программы
3.3 Метод Рунге-Кутта 4-го порядка
Этот метод наиболее часто применяется при программных расчетах и обычно его называют просто методом Рунге-Кутта. В данном методе используется разложение Тейлора до 4-го порядка включительно (рисунок 3.6):
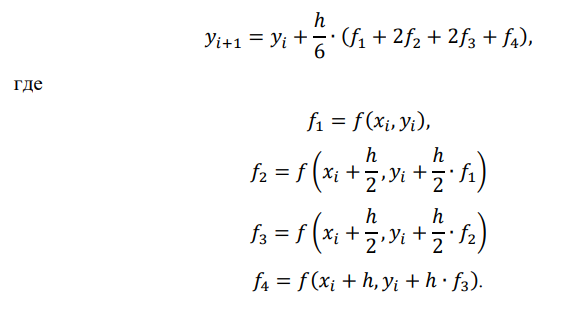
Рисунок 3.6 – Формула метода Рунге-Кутта 4-го порядка
Реализация метода Рунге-Кутта 4-го порядка на языке программирования C# изображена на рисунке 3.7.
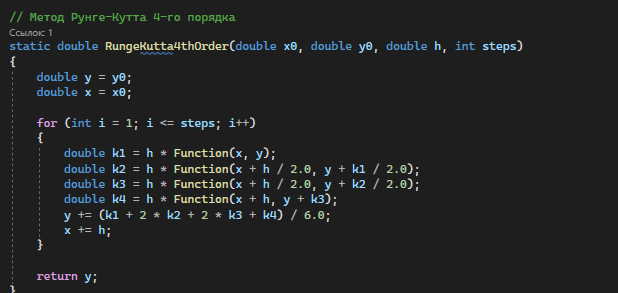
Рисунок 3.7 – Код программы
Результат работы программы всех 3х методов представлен на рисунке 3.8.
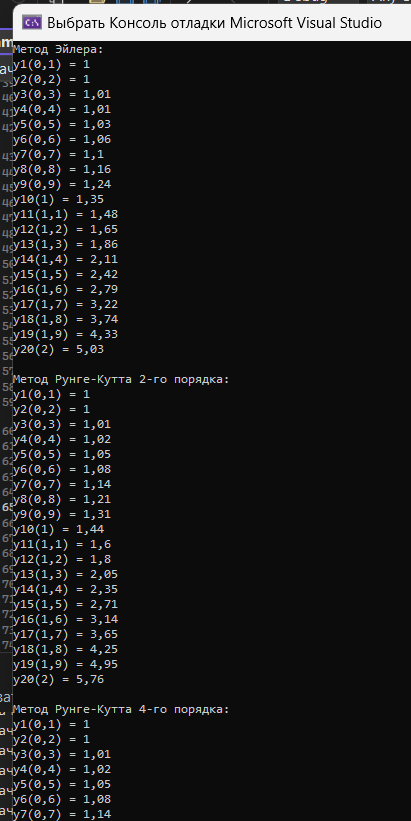
Рисунок 3.8 – Результат работы
Аналитическим методом получим точное решение: y=2ex-x2-2x-1
Таблица 3 – Полученные значения
Точное решение |
Решение методом Эйлера |
Решение методом Рунге-Кутта 2 порядка |
Решение методом Рунге-Кутта 4 порядка |
𝑦(𝑥0 ) |
𝑦̃1(𝑥0 ) |
𝑦̃2(𝑥0 ) |
𝑦̃4(𝑥0 ) |
y1(0,1) = 1 |
y1(0,1) = 1 |
y1(0,1) = 1 |
y1(0,1) = 1 |
y2(0,2) = 1 |
y2(0,2) = 1 |
y2(0,2) = 1 |
y2(0,2) = 1 |
y3(0,3) = 1,01 |
y3(0,3) = 1,01 |
y3(0,3) = 1,01 |
y3(0,3) = 1,01 |
y4(0,4) = 1,02 |
y4(0,4) = 1,01 |
y4(0,4) = 1,02 |
y4(0,4) = 1,02 |
y5(0,5) = 1,04 |
y5(0,5) = 1,03 |
y5(0,5) = 1,05 |
y5(0,5) = 1,05 |
y6(0,6) = 1,08 |
y6(0,6) = 1,06 |
y6(0,6) = 1,08 |
y6(0,6) = 1,08 |
y7(0,7) = 1,13 |
y7(0,7) = 1,1 |
y7(0,7) = 1,14 |
y7(0,7) = 1,14 |
y8(0,8) = 1,21 |
y8(0,8) = 1,16 |
y8(0,8) = 1,21 |
y8(0,8) = 1,21 |
y9(0,9) = 1,3 |
y9(0,9) = 1,24 |
y9(0,9) = 1,31 |
y9(0,9) = 1,31 |
y10(1) = 1,43 |
y10(1) = 1,35 |
y10(1) = 1,44 |
y10(1) = 1,44 |
y11(1,1) = 1,59 |
y11(1,1) = 1,48 |
y11(1,1) = 1,6 |
y11(1,1) = 1,6 |
y12(1,2) = 1,8 |
y12(1,2) = 1,65 |
y12(1,2) = 1,8 |
y12(1,2) = 1,8 |
y13(1,3) = 2,04 |
y13(1,3) = 1,86 |
y13(1,3) = 2,05 |
y13(1,3) = 2,05 |
y14(1,4) = 2,35 |
y14(1,4) = 2,11 |
y14(1,4) = 2,35 |
y14(1,4) = 2,35 |
y15(1,5) = 2,71 |
y15(1,5) = 2,42 |
y15(1,5) = 2,71 |
y15(1,5) = 2,71 |
y16(1,6) = 3,14 |
y16(1,6) = 2,79 |
y16(1,6) = 3,14 |
y16(1,6) = 3,15 |
y17(1,7) = 3,65 |
y17(1,7) = 3,22 |
y17(1,7) = 3,65 |
y17(1,7) = 3,66 |
y18(1,8) = 4,25 |
y18(1,8) = 3,74 |
y18(1,8) = 4,25 |
y18(1,8) = 4,26 |
y19(1,9) = 4,96 |
y19(1,9) = 4,33 |
y19(1,9) = 4,95 |
y19(1,9) = 4,96 |
y20(2) = 5,77 |
y20(2) = 5,03 |
y20(2) = 5,76 |
y20(2) = 5,78 |
Для каждого численного решения был построен совместный график полученной последовательности 𝑦̃ (𝑥𝑖) и точного решения 𝑦(𝑥) (рисунок 3.9).
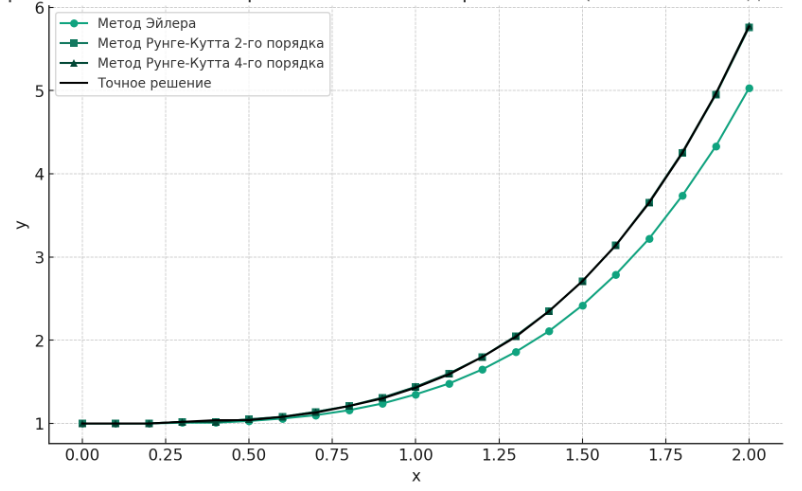
Рисунок 3.9 – График последовательностей
Как видно на рисунке, методы Рунге-Кутта 2-го и 4-го порядка сильно отличаются по точности от метода Эйлера, по той причине, что метод Эйлера самый простой и при этом самый неточный метод. Также методы Рунге-Кутта практически совпадают с точным решением, чуть ли не идентичны.