Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Отчет по лабораторной работе №4

по дисциплине «Численные методы»

Студент гр. 712-2 ___________ Л.С. Болтушкин ___________

Руководитель Старший преподаватель

_______ __________ Е.С. Катаева

__________

Томск 2023

Введение

Целью данной работы является освоение вычислительных методов нахождения определенного интеграла и исследования точности вычислений при разном числе разбиений, освоение и изучение точности метода численного дифференцирования, а также изучение метода группы Рунге-Кутта для численного решения дифференциального уравнения первого порядка (задачи Коши).

1 Ход работы

1.1 Численное интегрирование

В тестовом вопросе № 1 дан определенный интеграл. Необходимо составить программу, вычисляющую его значения следующими методами:

• методом левых прямоугольников;

• методом правых прямоугольников;

• методом трапеций;

• методом Симпсона.

Задать числа разбиений 𝑛 следующие: 6, 40, 120, 400. Число разбиений не должно увеличиваться в процессе вычисления интеграла – то есть перед применением формулы нужно вычислить узлы, и далее работать только с ними, без пересчета.

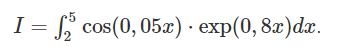
Рисунок 1.1 – Определенный интеграл

1.2 Метод левого прямоугольника

Для решения данного метода применяется формула метода левых прямоугольников, изображенная на рисунке 1.2, где h – шаг сетки (рисунок 1.3).

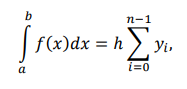
Рисунок 1.2 – Формула метода левых прямоугольников

Рисунок 1.3 – Вычисление шага сетки

Ниже представлен листинг метода (рисунок 1.4).

Рисунок 1.4 – Код программы

1.3 Метод правого прямоугольника

Для решения данного метода применяется формула метода правых прямоугольников, изображенная на рисунке 1.5. По сути, это идентичная формула с методом левого прямоугольника, только за место i=0 будет i=1 и из n не будет вычитаться единица.

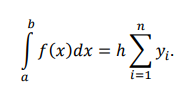
Рисунок 1.5 – Формула метода левых прямоугольников

Такие же незначительные изменения были и в самом коде (рисунок 1.6).

Рисунок 1.6 – Код программы

1.4 Метод трапеций

Для решения данного метода применяется формула метода трапеций, изображенная на рисунке 1.7.

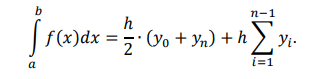
Рисунок 1.7 – Формула метода трапеций

Код метода представлен на изображении ниже (рисунок 1.8).

Рисунок 1.8 – Код программы

1.5 Метод Симпсона

Для решения данного метода применяется формула метода Симпсона, изображенная на рисунке 1.9.

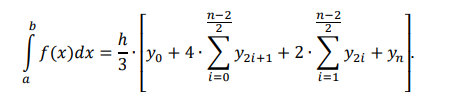
Рисунок 1.9 – Формула метода Симпсона

Код метода представлен на изображении ниже (рисунок 1.10).

Рисунок 1.10 – Код программы

Результат работы программы всех методов представлен ниже (рисунок 1.11).

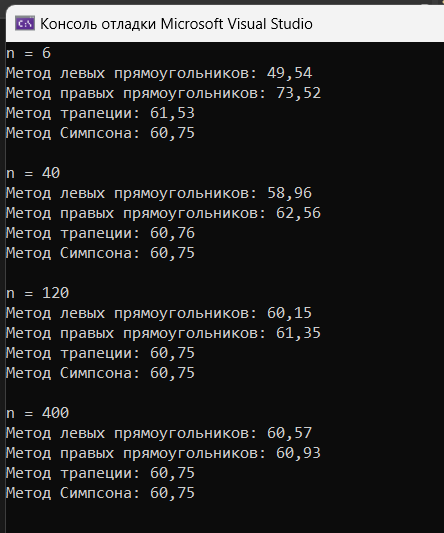
Рисунок 1.11 – Работа программы

Таблица 1 – Результаты программы

Метод	n=6	n=40	n=120	n=400
Метод левого прямоугольника	49,54	58,96	60,15	60,57
Метод правого прямоугольника	73,52	62,56	61,35	60,93
Метод трапеций	61,53	60,76	60,75	60,75
Метод Симпсона	60,75	60,75	60,75	60,75

Скорее всего, для меня метод левых и правых прямоугольников оказался более предпочтительным из-за соображений написания кода, по структуре кода данные методы были менее простыми.