Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ФУНКЦИИ ПО ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК

Отчет по лабораторной работе №3

по дисциплине «Численные методы»

Студент гр. 712-2 ___________ Л.С. Болтушкин ___________

Руководитель Старший преподаватель

_______ __________ Е.С. Катаева

__________

Томск 2023

Введение

Целью данной работы является освоение интерполяции и аппроксимации функций по последовательности точек.

Задание:

Необходимо рассчитать:

1) интерполяционный полином Лагранжа L2(x);

2) аппроксимирующую функцию f(x)=ax^2+bx+c, для индивидуальной

последовательности точек из тестового вопроса.

Порядок действий:

1. Запрограммировать кусочное вычисление интерполяционного полинома Лагранжа L2(x) по заданным узлам. Программа должна отвечать следующим условиям:

• должна быть возможность вычисления в любой точке отрезка [0;2.8], то есть полиномы должны рассчитываться для любых трех точек, стоящих рядом - например, если расчеты выполнены только для первых трех узлов, а для других отрезков требуется изменение скрипта, то такая программа не будет принята.

• выбирать узлы на расстоянии нельзя, такая программа не будет принята.

• не принимается программа, в которой построен полином более высокой степени.

• должна быть реализована возможность прогноза с помощью полинома Лагранжа, то есть для значения аргумента x>2.8 (с использованием данных в тесте точек, без вычисления новых узлов).

2. Запрограммировать реализацию метода наименьших квадратов для вычисления параметров функции f(x)=ax^2+bx+c, аппроксимирующей узловые точки.

Метод должен быть реализован самостоятельно - встроенные функции, вычисляющие коэффициенты, использовать можно только для сравнения и проверки результатов. Программа должна выдавать аналитический вид аппроксимирующей функции и включать в себя возможность вычисления этой функции в любой точке - узловой или прогнозной.

1 Ход работы

1.1 Интерполяция и аппроксимация функции по последовательности точек

Для того чтобы приступить к выполнению данной лабораторной, надо задать индивидуальную последовательность точек с помощью теста в электронном курсе (рисунок 1.1).

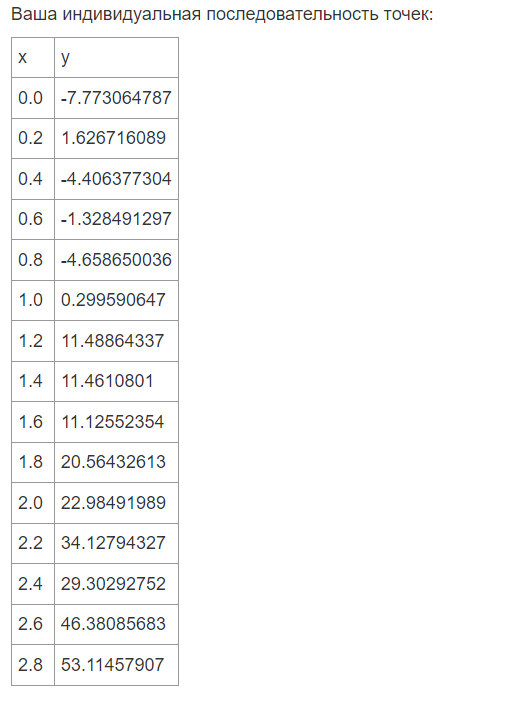
Рисунок 1.1 - Индивидуальная последовательность точек для задания

Для реализации первой части задания, нужно было написать код, который выполняет интерполяцию полинома Лагранжа для х, который задаётся с клавиатуры (рисунок 1.2).

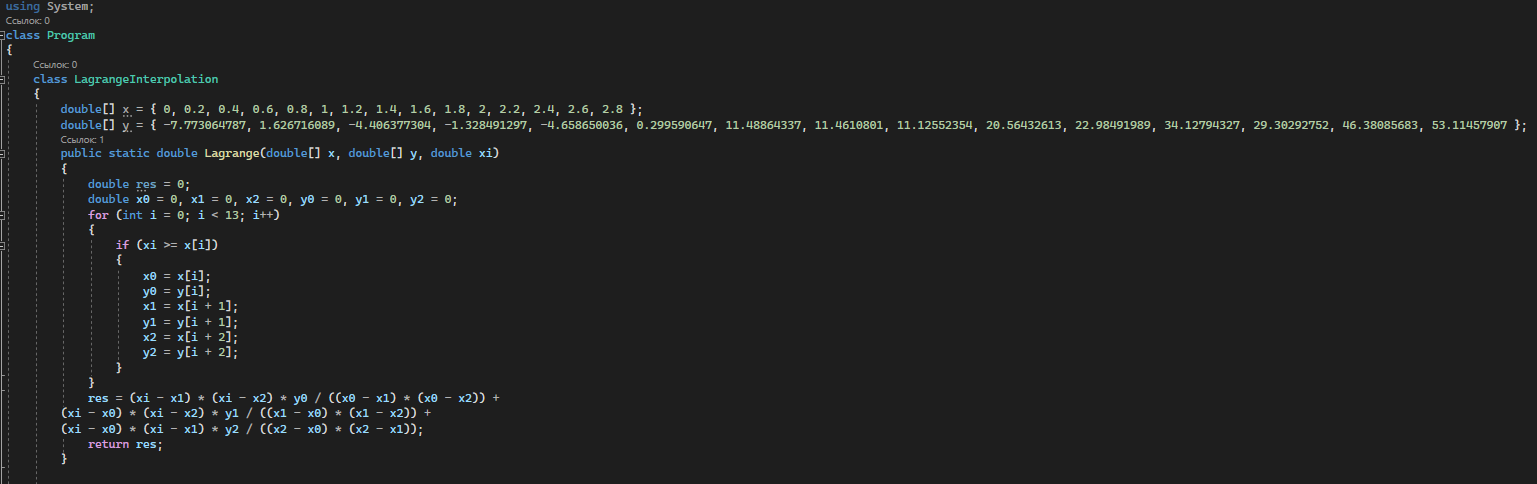
Рисунок 1.2 - Интерполяция полинома Лагранжа

По заданию нам нужно составить функцию f=ax^2+bx+c, где нам не известно a, b и с. Для нахождения воспользуемся методом Гаусса (рисунок 1.3)

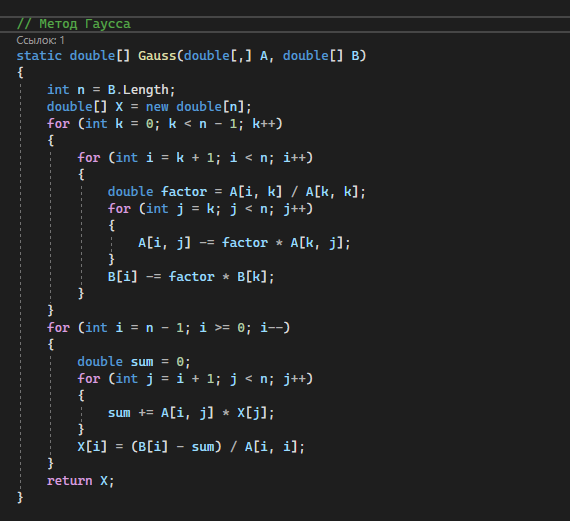
Рисунок 1.3 – Метод Гаусса

Результат работы метода Гаусса представлен на рисунке 1.4

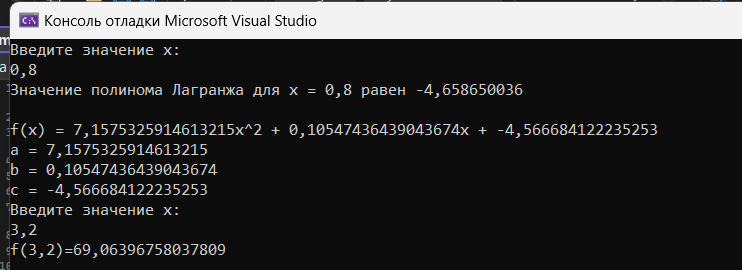
Рисунок 1.4 – Результат работы

После запуска программы, были сравнены значения точек, которые были даны изначально и получены в ходе выполнения лабораторной работы.

Таблица 1.1 – Сравнение значений

x	y индивидуальный	у результаты программа
0.0	- 7.773064787	-7,773064787
0.2	1.626716089	1,6267160889999999
0.4	- 4.406377304	-4,406377304
0.6	- 1.328491297	-1,328491297
0.8	- 4.658650036	-4,658650036
1.0	0.299590647	0,299590647
1.2	11.48864337	11,48864337
1.4	11.4610801	11,4610801
1.6	11.12552354	11,12552354
1.8	20.56432613	20,56432613
2.0	22.98491989	22,98491989
2.2	34.12794327	34,12794327
2.4	29.30292752	29,30292752
2.6	46.38085683	46,38085683
2.8	53.11457907	53,11457906999999

Также по заданию нужно было построить график по точкам, которые были даны нам в начале (рисунок 1.5).

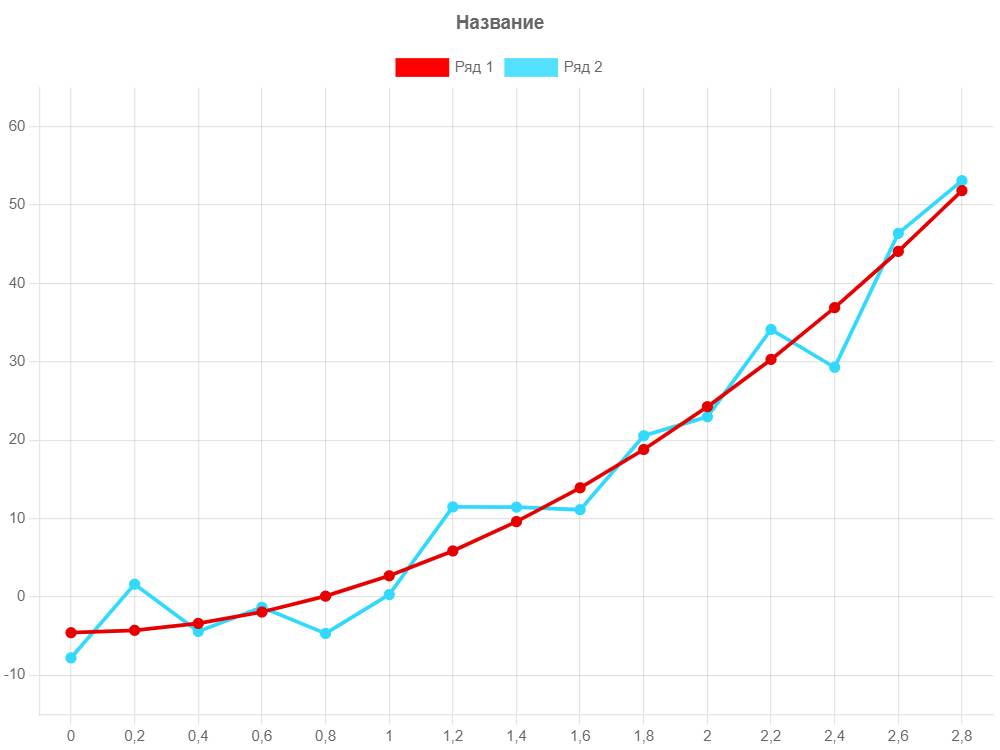
Рисунок 1.5 – График

В таблице 1.2 представлены данные, полученные в итоге запуска программы.

Таблица 1.2 - Результаты работы

0.8	-4,658650036	0,09851622781234237
1.7	16,72220093875	16,297891486551705
3.2	35,54940234	69,06396758037809
5.8	-1087,18443573	236,82446356798812

Заключение

В ходе выполнения данной лабораторной работы были получены навыки реализации интерполяции и аппроксимации функции по последовательности точек.

Приложение А

(обязательное)

using System;

class Program

{

class LagrangeInterpolation

{

double[] x = { 0, 0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4, 2.6, 2.8 };

double[] y = { -7.773064787, 1.626716089, -4.406377304, -1.328491297, -4.658650036, 0.299590647, 11.48864337, 11.4610801, 11.12552354, 20.56432613, 22.98491989, 34.12794327, 29.30292752, 46.38085683, 53.11457907 }; // Вычисление значения интерполяционного полинома Лагранжа в точке x

public static double Lagrange(double[] x, double[] y, double xi)

{

double res = 0;

double x0 = 0, x1 = 0, x2 = 0, y0 = 0, y1 = 0, y2 = 0;

for (int i = 0; i < 13; i++)

{

if (xi >= x[i])

{

x0 = x[i];

y0 = y[i];

x1 = x[i + 1];

y1 = y[i + 1];

x2 = x[i + 2];

y2 = y[i + 2];

}

}

res = (xi - x1) * (xi - x2) * y0 / ((x0 - x1) * (x0 - x2)) +

(xi - x0) * (xi - x2) * y1 / ((x1 - x0) * (x1 - x2)) +

(xi - x0) * (xi - x1) * y2 / ((x2 - x0) * (x2 - x1));

return res;

}

static void Main(string[] args)

{

double[] x = { 0, 0.2, 0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4, 2.6, 2.8 };

double[] y = { -7.773064787, 1.626716089, -4.406377304, -1.328491297, -4.658650036, 0.299590647, 11.48864337, 11.4610801, 11.12552354, 20.56432613, 22.98491989, 34.12794327, 29.30292752, 46.38085683, 53.11457907 }; // Вычисление значения интерполяционного полинома Лагранжа в точке x

Console.WriteLine("Введите значение x: ");

double xi = Convert.ToDouble(Console.ReadLine());

double LagrangeValue = Lagrange(x, y, xi);

Console.WriteLine("Значение полинома Лагранжа для x = {0} равен {1}", xi, LagrangeValue);

Console.WriteLine(" ");

// Вычисление суммы

int n = x.Length;

double sumX = 0,

sumX2 = 0,

sumX3 = 0,

sumX4 = 0,

sumY = 0,

sumXY = 0,

sumX2Y = 0;

for (int i = 0; i < n; i++)

{

double xi1 = x[i];

double xi2 = xi1 * xi1;

double xi3 = xi2 * xi1;

double xi4 = xi3 * xi1;

double yi = y[i];

sumX += xi1;

sumX2 += xi2;

sumX3 += xi3;

sumX4 += xi4;

sumY += yi;

sumXY += xi1 * yi;

sumX2Y += xi2 * yi;

}

// Решение системы уравнений

double[,] A = { { sumX4, sumX3, sumX2 },

{ sumX3, sumX2, sumX },

{ sumX2, sumX, n } };

double[] B = { sumX2Y, sumXY, sumY };

double[] coefficients = Gauss(A, B);

// Вывод результатов

Console.WriteLine("f(x) = {0}x^2 + {1}x + {2}", coefficients[0], coefficients[1], coefficients[2]);

Console.WriteLine("a = {0}", coefficients[0]);

Console.WriteLine("b = {0}", coefficients[1]);

Console.WriteLine("c = {0}", coefficients[2]);

Console.WriteLine("Введите значение x: ");

double x1 = Convert.ToDouble(Console.ReadLine());

double x2;

x2 = coefficients[0] * x1 * x1 + coefficients[1] * x1 + coefficients[2];

double x3 = x2;

Console.WriteLine("f({0})={1}", x1, x3);

}

}

// Метод Гаусса

static double[] Gauss(double[,] A, double[] B)

{

int n = B.Length;

double[] X = new double[n];

for (int k = 0; k < n - 1; k++)

{

for (int i = k + 1; i < n; i++)

{

double factor = A[i, k] / A[k, k];

for (int j = k; j < n; j++)

{

A[i, j] -= factor * A[k, j];

}

B[i] -= factor * B[k];

}

}

for (int i = n - 1; i >= 0; i--)

{

double sum = 0;

for (int j = i + 1; j < n; j++)

{

sum += A[i, j] * X[j];

}

X[i] = (B[i] - sum) / A[i, i];

}

return X;

}

}