
Болтушкин Л.С., группа 712-2, лабораторная 2
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ (СНУ)
Отчет по лабораторной работе №2
по дисциплине «Численные методы»
Студент гр. 712-2 ___________ Л.С. Болтушкин ___________
Руководитель Старший преподаватель
_______ __________ Е.С. Катаева
__________
Томск 2023
Введение
Целью лабораторной работы является освоение методов отделения и уточнения решения систем нелинейных уравнений.
Задание:
1. С помощью построения графика нужно выделить область, где лежит решение системы.
2. Необходимо самостоятельно, без использования готовых функций, разработать программу, реализующую метод Ньютона.
3. Программу нужно протестировать на системе уравнений (рисунок 1.1), должно быть найдено за 10–15 итераций.
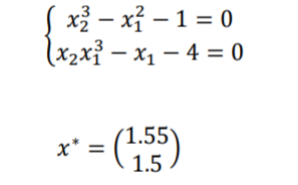
Рисунок 1.1 – Система уравнений и её решение
4. В рамках индивидуального задания нужно решить систему уравнений из вопроса №1 теста.
1 Ход работы
1.1 Решение СНУ
Для решения системы нелинейных уравнений с помощью метода Ньютона, нужно ввести саму систему в код программы, а также взять её производную по каждой из переменных. Кроме этого, задаётся начальное приближение для х1 и х2, точность нахождения решения и количество итераций равное 0 (рисунок 1.2).
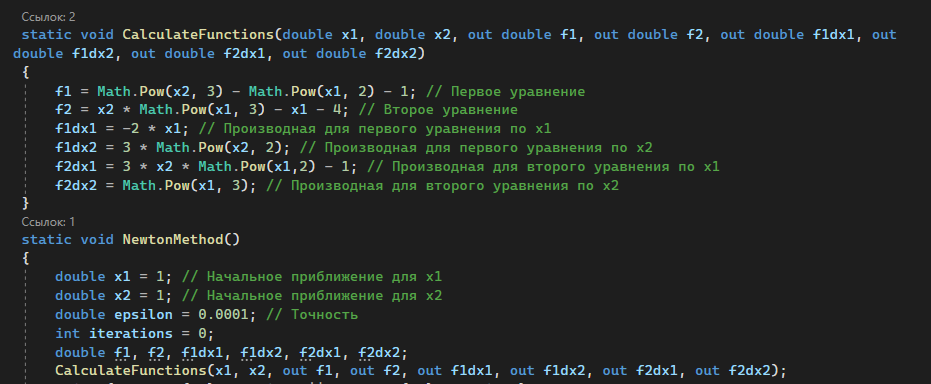
Рисунок 1.2 – Первая часть кода
В цикле применяется метод Ньютона, в том числе после каждого применения, обновление количества итераций.
После того, как была прописана основная часть кода, то перейдем к выводу решения и количества итераций (рисунок 1.3).
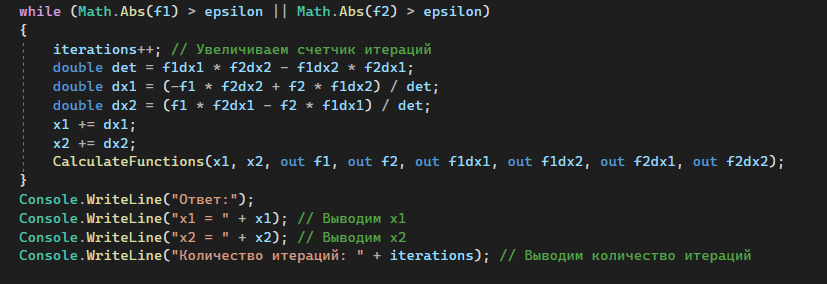
Рисунок 1.3 – Вторая часть кода
Чтобы проверить, работает ли программа, то подставим значения из системы нелинейных уравнений, которая дана нам в лабораторной работе (рисунок 1.4).
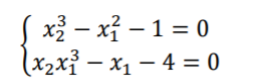
Рисунок 1.4 – Тестировочная система нелинейных уравнений
Результат работы программы на примере тестировочной системы нелинейных уравнений изображен на рисунке 1.5.
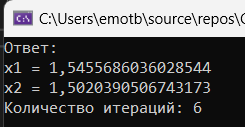
Рисунок 1.5 – Результат решения тестировочной системы
Также в лабораторной работе была система нелинейных уравнений, которая выдавалась случайном образом в тесте (рисунок 1.6).
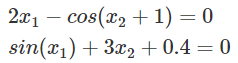
Рисунок 1.6 – Индивидуальная система нелинейных уравнений
Результат работы программы на примере индивидуальной системы нелинейных уравнений изображен на рисунке 1.7.
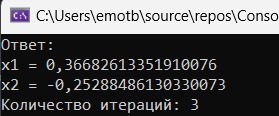
Рисунок 1.7 – Результат решения индивидуальной системы
Также, для данной системы нелинейных уравнений был построен график (рисунок 1.8).
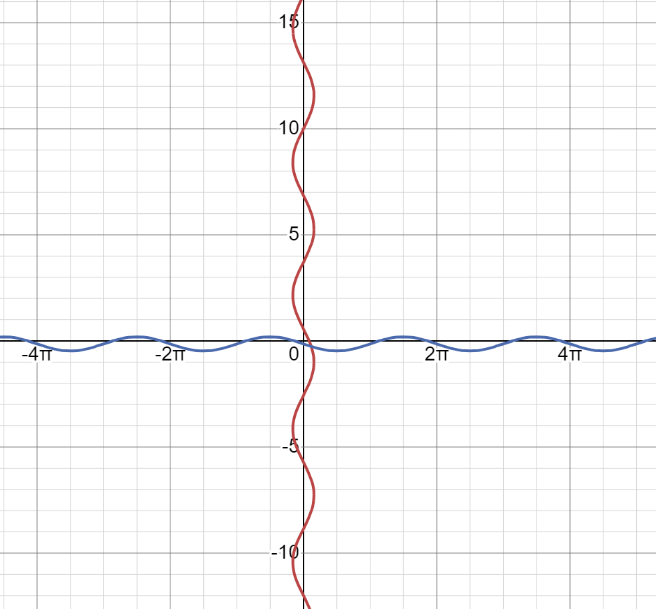
Рисунок 1.8 – График для индивидуальной системы нелинейных уравнений
В таблице 1.1 представлены данные, полученные в итоге решения программы по двум системам нелинейных уравнений.
Таблица 1.1 – Результат работы
|
Решение |
Начальная точка |
Число итераций |
Тестовая система |
x1=1,55 x2=1,5 |
0 |
6 |
Индивидуальная система |
x1=0,37 x2=-0,25 |
0 |
3 |
Заключение
В ходе выполнения данной лабораторной работы были изучены методы отделения и уточнения решения систем нелинейных уравнений, а также закрепление знаний решения методом Ньютона.
Приложение А
(обязательное)
using System;
using System.Net.Http.Headers;
namespace_2
{
internal class Program
{
static void CalculateFunctions(double x1, double x2, out double f1, out double f2, out double f1dx1, out
double f1dx2, out double f2dx1, out double f2dx2)
{
f1 = 2 * x1 - Math.Cos(x2 + 1); // Первое уравнение
f2 = Math.Sin(x1) + 3 * x2 + 0.4; // Второе уравнение
f1dx1 = 2; // Производная для первого уравнения по х1
f1dx2 = Math.Sin(x2 + 1); // Производная для первого уравнения по х2
f2dx1 = Math.Cos(x1); // Производная для второго уравнения по х1
f2dx2 = 3; // Производная для второго уравнения по х2
}
static void NewtonMethod()
{
double x1 = 1; // Начальное приближение для x1
double x2 = 1; // Начальное приближение для x2
double epsilon = 0.0001; // Точность
int iterations = 0;
double f1, f2, f1dx1, f1dx2, f2dx1, f2dx2;
CalculateFunctions(x1, x2, out f1, out f2, out f1dx1, out f1dx2, out f2dx1, out f2dx2);
while (Math.Abs(f1) > epsilon || Math.Abs(f2) > epsilon)
{
iterations++; // Увеличиваем счетчик итераций
double det = f1dx1 * f2dx2 - f1dx2 * f2dx1;
double dx1 = (-f1 * f2dx2 + f2 * f1dx2) / det;
double dx2 = (f1 * f2dx1 - f2 * f1dx1) / det;
x1 += dx1;
x2 += dx2;
CalculateFunctions(x1, x2, out f1, out f2, out f1dx1, out f1dx2, out f2dx1, out f2dx2);
}
Console.WriteLine("Ответ:");
Console.WriteLine("x1 = " + x1); // Выводим х1
Console.WriteLine("x2 = " + x2); // Выводим х2
Console.WriteLine("Количество итераций: " + iterations); // Выводим количество итераций
}
static void Main(string[] args)
{
NewtonMethod();
Console.ReadLine();
}
}
}
