
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ). ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ (НУ)
Отчет по лабораторной работе №1
по дисциплине «Численные методы»
Студент гр. 712-2 ___________ Л.С. Болтушкин ___________
Руководитель Старший преподаватель
_______ __________ Е.С. Катаева
__________
Томск 2023
Введение
Целью лабораторной работы является освоение методов решения систем линейных алгебраических уравнений и решения нелинейных уравнений с одной переменной.
Ход работы
1 Решение СЛАУ
1.1 Пример системы уравнений
Перед решением своего варианта программы нужно протестировать пример.
Для тестирования использовать систему уравнений, изображенная на рисунке 1.1.
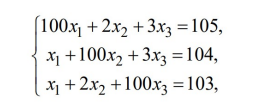
Рисунок 1.1 – Пример системы
Из каждого уравнения были выражены x1, x2, x3:
x1= (-2 * x2 – 3 * x3 + 105) / 100;
x2 = (-x1 - 3 * x3 +104) / 100;
x3 = (-x1 - 2 * x2 + 103) / 100.
На рисунке 1.2 представлена работа программы для тестировачной системы уравнений.
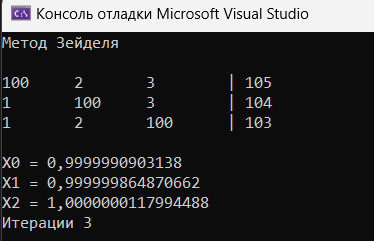
Рисунок 1.2 – Работа программы тестировочной системы
1.2 Индивидуальная система уравнений
На рисунке 1.3 представлена индивидуальная система уравнений.
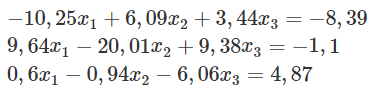
Рисунок 1.3 – Система уравнений
Из каждого уравнения были выражены х1, х2, х3:
x1= (-6,09 * x2 – 3,44 * x3 – 8,39) / -10,25;
x2 = (-9,64 * x1 – 9,39 * x3 -1,1) / -20,01;
x3 = (-0,6 * x1 + 0,94 * x2 + 4,87) / -6,06.
На рисунке 1.4 представлена работа программы для индивидуальной системы уравнений.
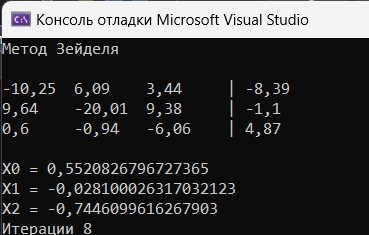
Рисунок 1.4 – Работа программы индивидуальной системы
Таблица 1 – Результаты решения тестировочной системы и индивидуальной системы.
|
Решение |
Начальная точка |
Число итераций |
Тестировочная система |
0,99; 0,99; 1. |
0; 0; 0. |
3 |
Индивидуальная система |
0,55; -0,02; -0,74. |
-8,39; -1,1; 4,87 |
8 |
2 Решение нелинейного уравнения
2.1 Отделение корня
Рассмотрим функцию F(х) = 0,33x2 + 0,98x + 0,68 и ее производную
F’(x) = 0,66x + 0,98. Найдем точки перегиба, то есть точки, где производная функции F’(x) = 0. Точка перегиба x = -1,48.
Для x < -1,48 значение производной отрицательно, а для x > -1,48 значение производной положительно. Значит, функция монотонно возрастает в интервале (-∞, -1,48) и монотонно убывает в интервале (-1,48, +∞). Таким образом, отрезок [-∞, -1,48] является отрезком, на котором функция монотонна и имеет ровно один корень. График функции изображен на рисунке 2.1.
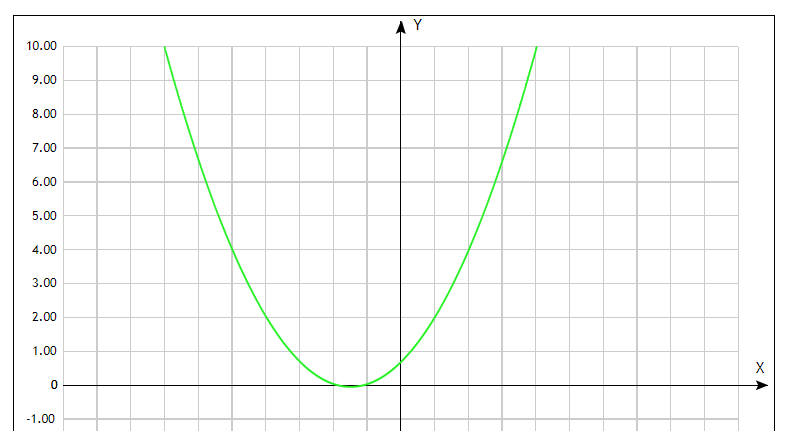
Рисунок 2.1 – График индивидуальной функции
2.2 Нахождение корня методом Ньютона
В данном методе сначала приводят касательную к функции в отрезке, выбранном пользователем, затем находится точка пересечения касательной с осью ОХ и эта точка будет первым приближением для искомого корня. Затем каждому последующему Х присваивается разница между Х на предыдущей итерации и делением функции от предыдущего Х на первую производную. Условие остановки определяется значением функции от Х на текущей итерации, если оно меньше Е, которое равно 0,01.
На рисунке 2.2 представлено решение методом Ньютона тестировочного уравнения, а на рисунке 2.3 решение тем же методом, только для индивидуальной функции.
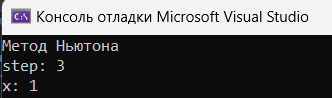
Рисунок 2.2 – Решение тестировочного уравнения
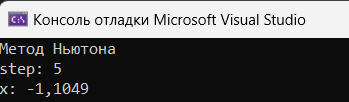
Рисунок 2.3 – Решение индивидуального уравнения
2.3 Нахождение корня методом простых итераций
В данном методе Х присваивается сумма Х, на предыдущей итерации, и произведения функции Х, на предыдущей итерации и L, которое ровно -2 деленому на первую производную от функции, Х на прошлой итерации. Программа останавливается, тогда, когда модуль разности Х будет меньше заданной точности.
На рисунке 2.4 представлено решение тестировочного уравнения с помощью метода простых итераций, на рисунке 2.5 решение тем же методом, только для индивидуальной функции.
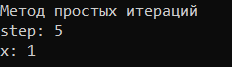
Рисунок 2.4 – Решение тестировочного уравнения
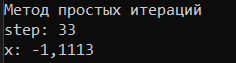
Рисунок 2.5 – Решение индивидуального уравнения
Таблица 2 – Результаты по тестировочному уравнению
Результаты Метод |
Начальная точка |
Число итераций, за которые найден корень |
Найденный корень |
Метод Ньютона |
0,5 |
3 |
1,00 |
Метод простых итераций |
0,5 |
5 |
1,00 |
Таблица 3 – Результаты по индивидуальному уравнению
Результаты Метод |
Начальная точка |
Число итераций, за которые найден корень |
Найденный корень |
Метод Ньютона |
0 |
5 |
-1,1049 |
Метод простых итераций |
0 |
33 |
-1,1113 |
