
Болтушкин Л.С., группа 712-2, практика 6
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
ГРАФЫ
Отчет по практической работе №6
по дисциплине «Структуры данных»
Студент гр. 712-2 ___________ Л.С. Болтушкин ___________
Руководитель Доцент кафедры КИБЭВС
_______ __________ Е.Е. Лунёва
__________
Томск 2023
Задание
Реализовать возможность работы с графом N узлов, M ребер. Выберете самостоятельно структуру. Обеспечьте следующие интерфейсные методы:
ввод графа (можно случайным образом, можно вводить с клавиатуры) НЕДОПУСТИМО работать только с конечным числом ребер и узлов. Приложение должно позволять вводить разные графы.
вывод графа - матрица смежности или весов
Вариант 6. По заданной системе дорог определить, есть ли в ней город, из которого можно добраться до каждого из остальных городов, проезжая не более N километров.
Содержание
Введение. 4
Основная часть. 5
Заключение. 10
Приложение А 11
Введение
Целью данной практической работы является реализование возможности работы с графом N узлов, M ребер. Так, чтобы была возможность ввод графа и вывод графа - матрица смежности или весов.
В данной работе будет использоваться такой язык программирования как
С#.
Основная часть
Для того, чтобы начать работу создадим класс "Graph", который представляет собой граф с N вершинами и M ребрами. Конструктор класса инициализирует переменные N и M, а также создает матрицу matrix с помощью метода Matrix() (рисунок 1.1).
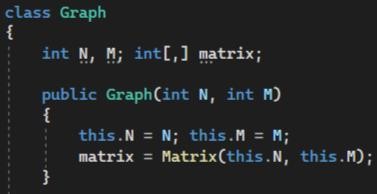
Рисунок 1.1 - Создание класса "Graph"
Далее создаётся двумерный массив размером NxN и заполняет его случайными числами от 1 до 25. Условие count1 < M гарантирует, что будет заполнено только M ячеек массива. Если i равно j (i == j), то значение в данной ячейке устанавливается равным 0. Затем возвращается заполненный массив. (рисунок 1.2).
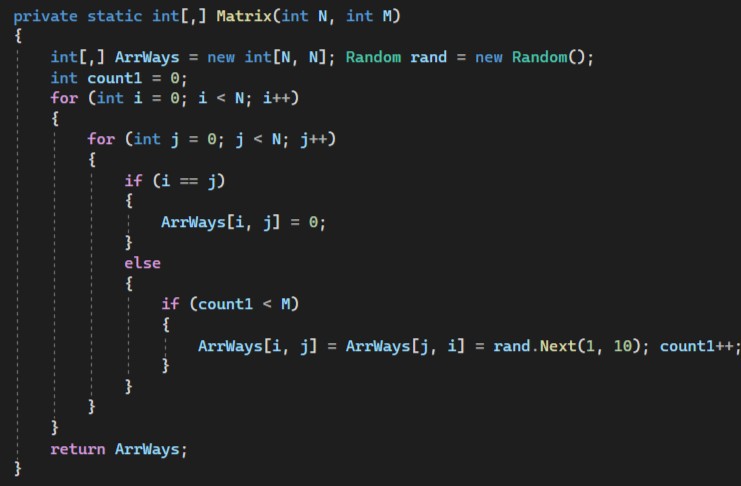
Рисунок 1.2 - Создание массива
Также необходимо прописать в программе метод Print(), который выводит матрицу весов на экран.
Метод использует двойной цикл (for) для доступа к элементам матрицы и выводит их значения на консоль. В конце каждой строки матрицы происходит переход на новую строку для более удобного отображения (рисунок 1.3).
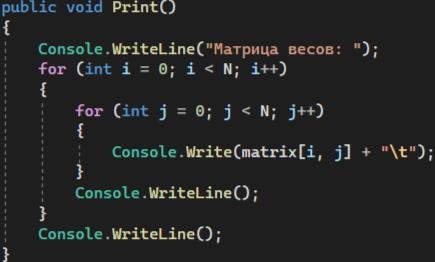
Рисунок 1.3 - метод Print()
Далее мы должны реализовать следующий метод: "Ways", который принимает параметр way типа int. Он используется для проверки возможности добраться из одного узла во все города в графе, представленного матрицей смежности matrix размером N x N.
Для каждого узла i в графе, метод инициализирует переменную countW в 0 и затем перебирает все другие узлы k в графе.
Если i и k не равны, а также значение в матрице смежности matrix[i, k] не равно 0 и меньше или равно значению параметра way, то countW увеличивается на 1.
Если условие не выполняется, то цикл прерывается с помощью оператора break. После выборки всех узлов, проверяется, равно ли значение countW числу N - 1 (количество узлов в графе минус 1).
Если это условие выполняется, выводится сообщение, указывающее, что из узла i можно добраться во все города (рисунок 1.4)
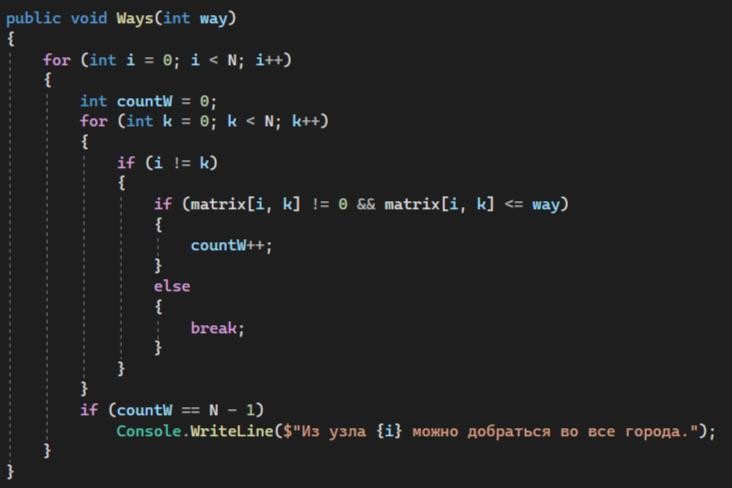
Рисунок 1.4 - Метод "Ways"
Предпоследним действием мы реализуем алгоритм поиска кратчайшего пути в графе, ограниченного максимальной длиной пути maxDistance от начальной вершины start.
Создаём список shortestPath, который будет содержать вершины кратчайшего пути, а также создаём очередь. Начальная вершина start добавляется в очередь с расстоянием 0 и начальным путем, состоящим только из этой вершины. Далее выполняется основной цикл while (queue.Count > 0), который продолжает выполнение до тех пор, пока очередь не пуста. Затем происходит перебор соседних вершин в графе с помощью цикла for (int i = 0; i < N; i++).
Если все условия выполняются, создается новый путь newPath, который является копией текущего пути currentPath, но с добавленной вершиной i. Также
вычисляется новое расстояние newDistance, добавляя вес ребра между текущей и вершиной i к текущему расстоянию. Если новое расстояние newDistance не превышает maxDistance и длина пути newPath равна общему количеству вершин N, то это означает, что был найден путь, соответствующий заданным критериям (рисунок 1.6).
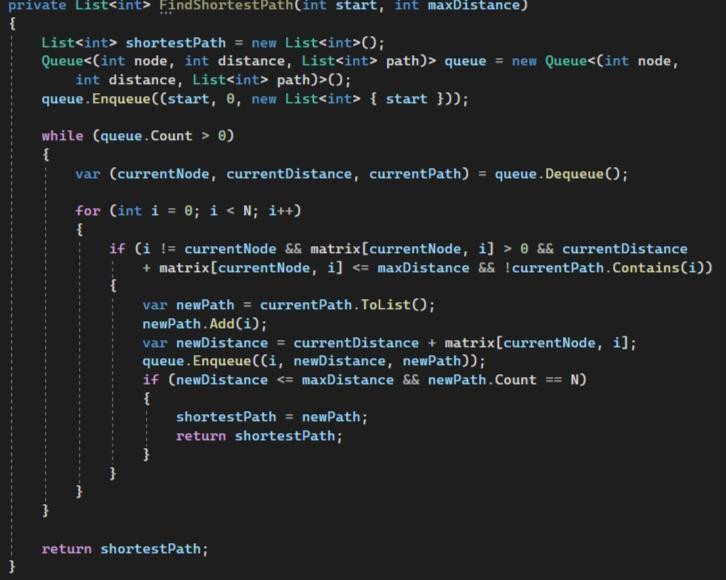
Рисунок 1.5 - Поиск наикратчайшего пути
И в последнем действие я создаю и инициализирую объект класса Graph с заданным количеством узлов и ребер. Затем алгоритм печатает граф, запрашивает величину пути от пользователя и вызывает метод Ways() класса Graph с переданным параметром "way".(рисунок 1.6)
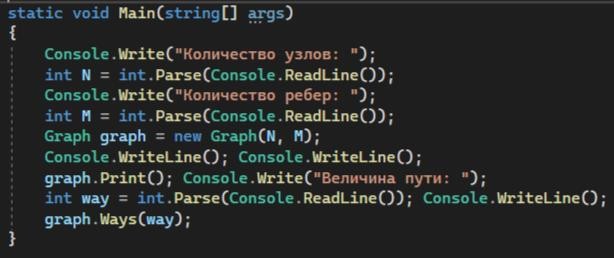
 Рисунок
1.6 - Создание и инициализация объекта
класса Graph Результат
работы кода
представлен на
рисунке 1.7.
Рисунок
1.6 - Создание и инициализация объекта
класса Graph Результат
работы кода
представлен на
рисунке 1.7.
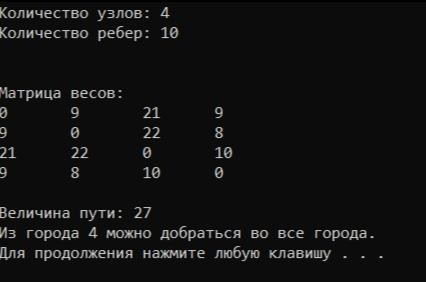
Рисунок 1.7 - Результат работы кода В приложении А представлен листинг программы.
Заключение
В ходе выполнения данной лабораторной работы были реализованы возможности работы с графом N узлов, M ребер. Так, чтобы была возможность ввод графа и вывод графа - матрица смежности или весов.
Приложение А
(обязательное)
using System;
using System.Collections.Generic; using System.Linq;
using System.Security.Cryptography;
namespace ShortestPath
{
class Program
{
class Graph
{
int N, M; int[,] matrix;
public Graph(int N, int M)
{
this.N = N; this.M = M;
matrix = Matrix(this.N, this.M);
}
private static int[,] Matrix(int N, int M)
{
int[,] ArrWays = new int[N, N]; Random rand = new Random(); int count1 = 0;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
if (i == j)
{
ArrWays[i, j] = 0;
}
else
{
if (count1 < M)
{
ArrWays[i, j] = ArrWays[j, i] = rand.Next(1, 25); count1++;
}
}
}
}
return ArrWays;
}
public void Print()
{
Console.WriteLine("Матрица весов:"); for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
Console.Write(matrix[i, j] + "\t");
}
Console.WriteLine();
}
Console.WriteLine();
}
public void Ways(int way)
{
for (int i = 0; i < N; i++)
{
int countW = 0;
for (int k = 0; k < N; k++)
{
if (i != k)
{
if (matrix[i, k] != 0 && matrix[i, k] <= way)
{
countW++;
}
else
{
break;
}
}
}
if (countW == N - 1)
Console.WriteLine($"Из города {i + 1} можно добраться во все города.");
}
}
private List<int> FindShortestPath(int start, int maxDistance)
{
List<int> shortestPath = new List<int>();
Queue<(int node, int distance, List<int> path)> queue = new Queue<(int node, int distance, List<int> path)>();
queue.Enqueue((start, 0, new List<int> { start }));
while (queue.Count > 0)
{
var (currentNode, currentDistance, currentPath) = queue.Dequeue();
for (int i = 0; i < N; i++)
{
if (i != currentNode && matrix[currentNode, i] > 0 && currentDistance
+ matrix[currentNode, i] <= maxDistance && !currentPath.Contains(i))
{
var newPath = currentPath.ToList(); newPath.Add(i);
var newDistance = currentDistance + matrix[currentNode, i]; queue.Enqueue((i, newDistance, newPath));
if (newDistance <= maxDistance && newPath.Count == N)
{
shortestPath = newPath; return shortestPath;
}
}
}
}
return shortestPath;
}
}
static void Main(string[] args)
{
Console.Write("Количество узлов: "); int N = int.Parse(Console.ReadLine()); Console.Write("Количество ребер: "); int M = int.Parse(Console.ReadLine()); Graph graph = new Graph(N, M); Console.WriteLine(); Console.WriteLine();
graph.Print(); Console.Write("Величина пути: ");
int way = int.Parse(Console.ReadLine()); Console.WriteLine();
graph.Ways(way);
}
}
}
