
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА
Отчет по практической работе №5
по дисциплине «Структуры данных»
Студент гр. 712-2 ___________ Л.С. Болтушкин ___________
Руководитель Доцент кафедры КИБЭВС
_______ __________ Е.Е. Лунёва
__________
Томск 2023
Задание
Реализовать бинарное дерево поиска при помощи динамических структур (классы). Предусмотреть следующие интерфейсные методы:
1) Инициализация пустого дерева.
2) Добавление элемента в дерево bool AddItem (int a) - возвращает true, если добавление прошло успешно, иначе false. Например, если такой элемент уже был в дереве - то метод вернет false.
3) Удаление элемента из дерева. bool RemoveItem (int a)
4) Очистка дерева void Clear()
5) Вывод дерева (используйте поиск в ширину) void Print() или string Print()
Вариант 6: Реализуйте метод, рассчитывающий степень дерева.
Содержание
Задание 2
Введение 4
1 Ход работы 5
1.1 Описание класса Tree 5
1.2 Описание реализации задания по варианту 12
1.3 Результат работы программы 14
Заключение 15
Приложение А 16
Введение
Целью работы является реализация бинарного дерева при помощи динамических структур.
Программа будет разработана на языке программирования C#.
1 Ход работы
Дерево – это граф без петель и циклов. Деревья используются для организации данных в виде иерархической структуры. Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел – дочерним.
Листья – это последние узлы на дереве.
Листинг программы представлен в Приложении А.
1.1 Описание класса Tree
Для добавления элемента в дерево используется метод AddItem. Он сравнивает значение добавляемого элемента с существующим, и если значение элемента больше существующего, выполняется проверка на наличие правого поддерева, и, если оно отсутствует, элемент записывается вправо, иначе происходит вызов функции AddItem для следующего правого элемента.
Если же добавляемый элемент меньше существующего, выполняется проверка на наличие левого поддерева, и, если оно отсутствует, элемент записывается влево, иначе происходит вызов функции AddItem для следующего левого элемента.
Данное действие представлено на рисунке 1.1

Рисунок 1.1 - Метод AddItem
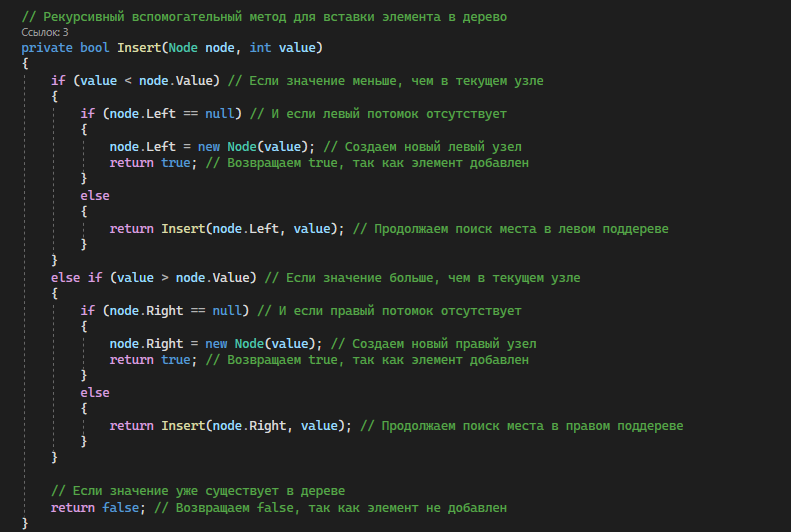
Рисунок 1.2 – Метод Insert.
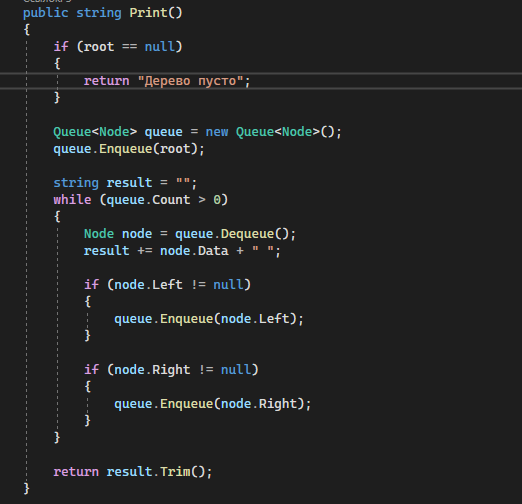
Рисунок 1.3 - Метод Print
Если удаляемый элемент не содержит левого поддерева, на его место становится следующий элемент от правого поддерева.
Если же элемент имеет поддеревья с обоих сторон, на его место становится наименьший элемент из правого поддерева.
Данное действие представлено на рисунке 1.4.
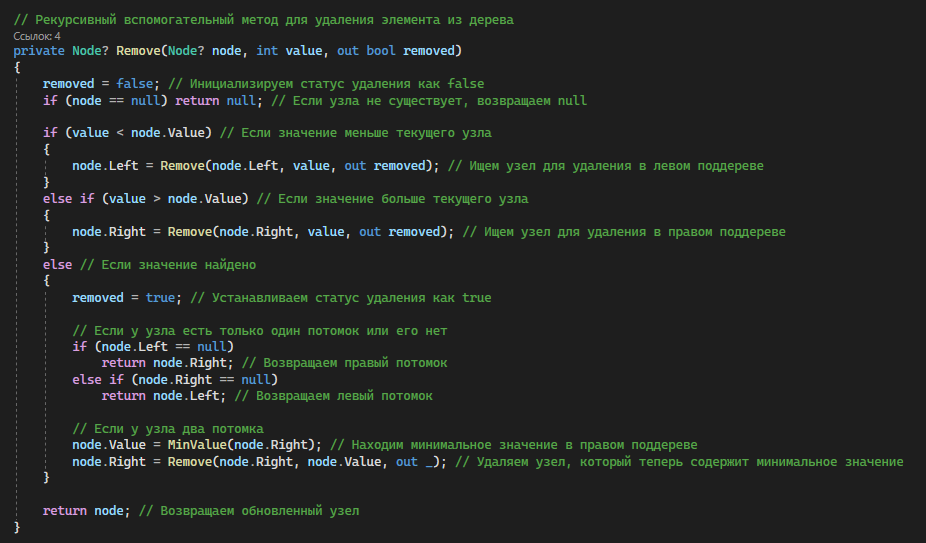
Рисунок 1.4 – Метод RemoveItem
Для того чтобы очистить список просто возвращаем значение «null». Данное действие представлено на рисунке 1.6

Рисунок 1.6 – Метод Clear
Для печати значений дерева используем метод – Enqueue (рисунок 1.7).
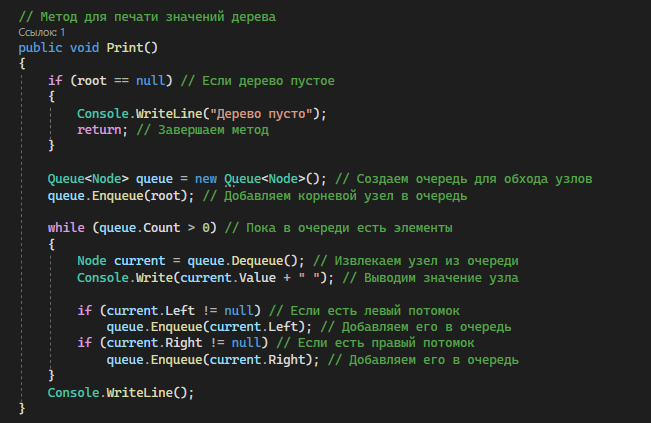
Рисунок 1.7 – Метод Enqueue
1.2 Удаление узлов из дерева
У удаляемого узла нет левого и правого поддерева. В данной ситуации просто удаляется данный лист (узел).
Данное действие представлено на рисунке 1.8
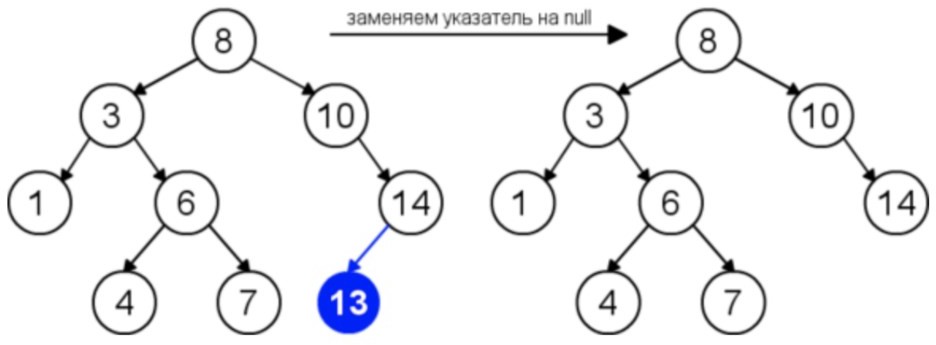
Рисунок 1.8 - У удаляемого узла нет левого и правого поддерева
У удаляемого узла одно поддерево. В данной ситуации удаляется данный узел, а на его место ставим поддерево.
Удаляем элемент, а на его место ставим либо самый правый элемент его левого поддерева, либо самый левый его правого поддерева.
Данное действие представлено на рисунке 1.9.
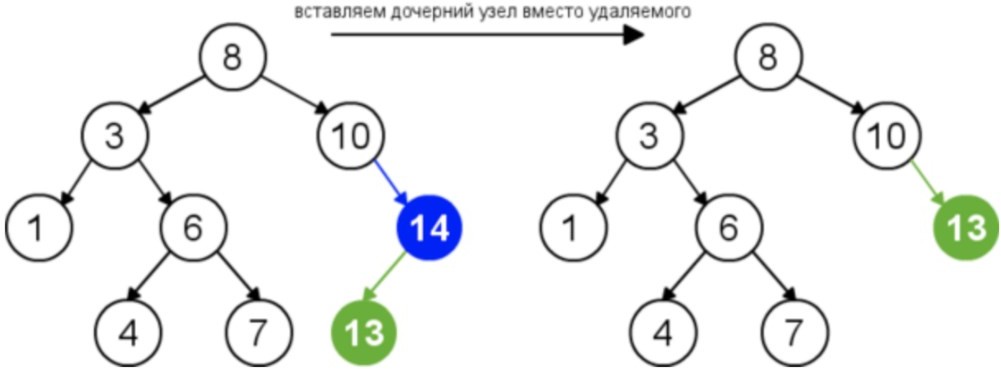
Рисунок 1.9 - У удаляемого узла одно поддерево
Самый сложный случай: у удаляемого узла существуют оба поддерева. В данной ситуации необходимо сначала найти следующий за удаляемым элемент, а потом его поставить на место удаляемого элемента.
Удаляем элемент, а на его место ставим либо самый правый элемент его левого поддерева, либо самый левый его правого поддерева.
Данное действие представлено на рисунке 1.10.
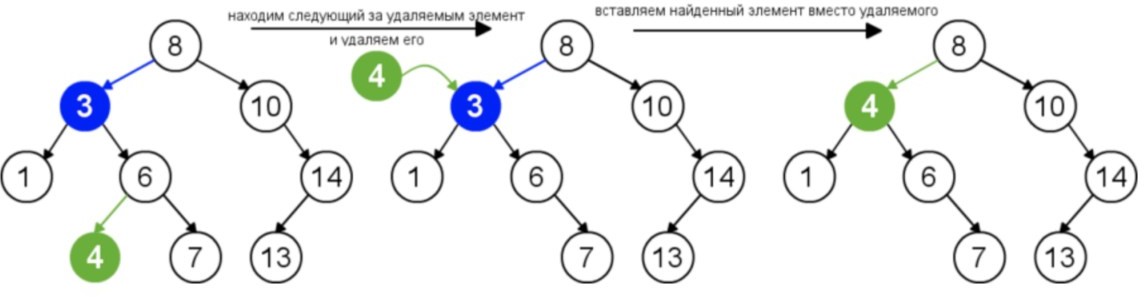
Рисунок 1.10 - У удаляемого узла существуют оба поддерева
Работа программы представлена на рисунке 1.11.
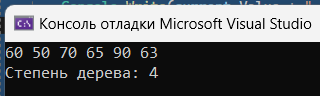
Рисунок 1.11 – Результат работы программы
