Болтушкин Л.С., группа 712-2, лабораторная 2

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

МИНИМИЗАЦИЯ ФУНКЦИИ БЕЗ ОГРАНИЧЕНИЯ НА ПЕРЕМЕННЫЕ

Отчет по лабораторной работе №2

по дисциплине «Методы оптимизации»

Студент гр. 712-2 ___________ Л.С. Болтушкин ___________

Руководитель Старший преподаватель

_______ __________ Е.С. Катаева

__________

Томск 2023

Введение

Целью данной работы является освоение минимизации функции без ограничения на переменные, а также нахождение минимума функции Розенброка, глобальный минимум функции Била и глобальный минимум функции Швефеля.

1 Ход работы

1.1 Минимум функции Розенброка

В тестовом вопросе № 1 дана функция. Необходимо составить программу, вычисляющую его минимум.

Рисунок 1.1 – Функция Розенброка

Функция Розенброка, известная также как "долина Розенброка", является популярной тестовой функцией для алгоритмов оптимизации. На рисунке ниже изображена формула, которая использовалась в написании кода, где a = 1 и b = 100, глобальный минимум этой функции достигается при x = a и y = a².

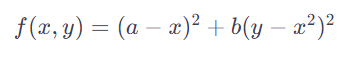
Рисунок 1.2 – Формула Розенброка

Ниже представлен результат работы программы, листинг кода находится в приложении А (рисунок 1.3).

Рисунок 1.3 – Результат работы

Также для данной функции был построен график (рисунок 1.4).

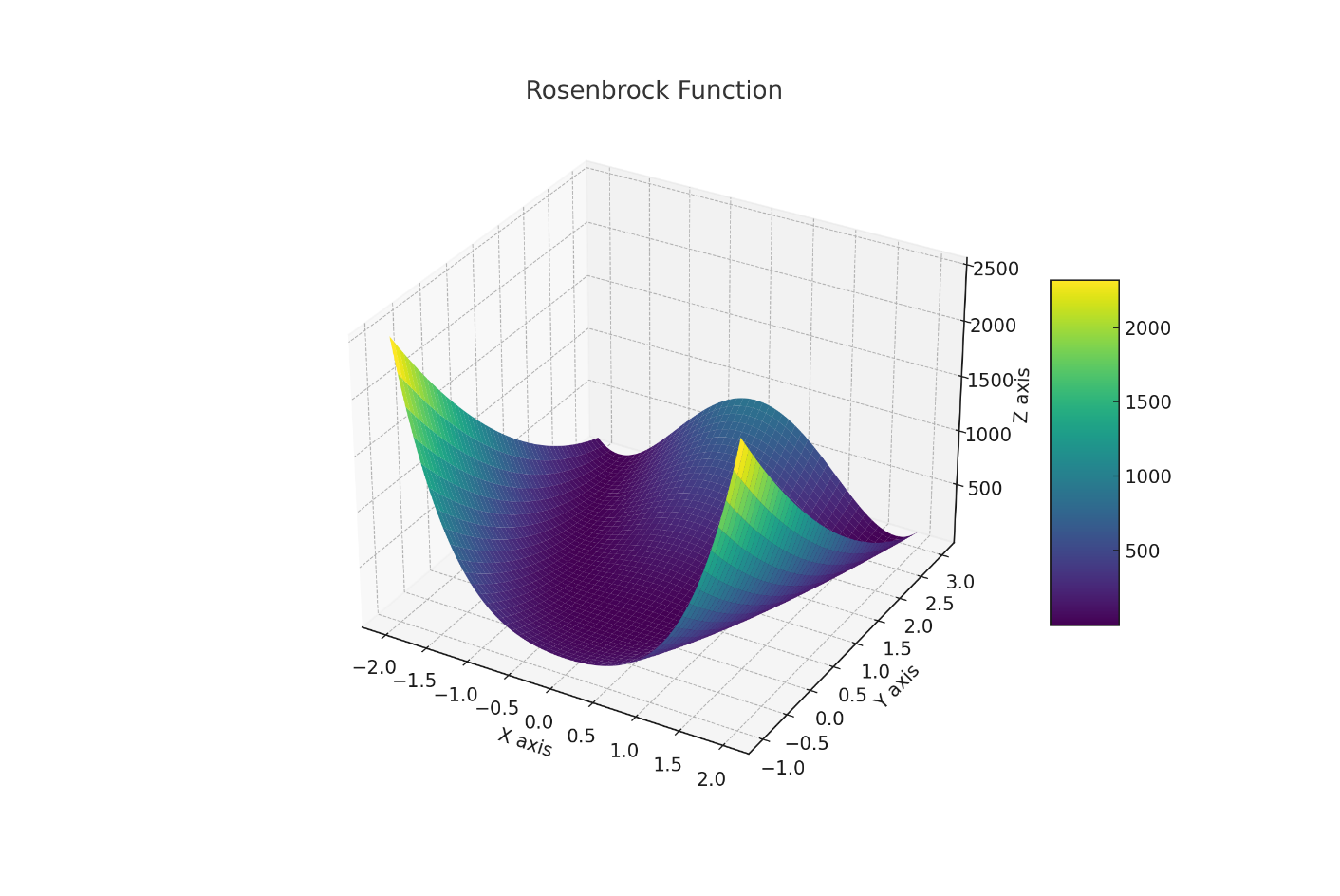
Рисунок 1.4 – График функции Розенброка

1.2 Глобальный минимум функции Била

В тестовом вопросе № 2 дана функция. Необходимо составить программу, вычисляющую его глобальный минимум.

Рисунок 1.5 – Функция Била

Для написания кода данной функции было использовано подключение внешней библиотеки MathNet.Numerics, для того, чтобы использовать такие функции, как ObjectiveFunction и BfgsBMinimize.

Ниже представлен результат работы программы, листинг кода находится в приложении Б (рисунок 1.6).

Рисунок 1.6 – Результат работы

Также для данной функции был построен график (рисунок 1.7).

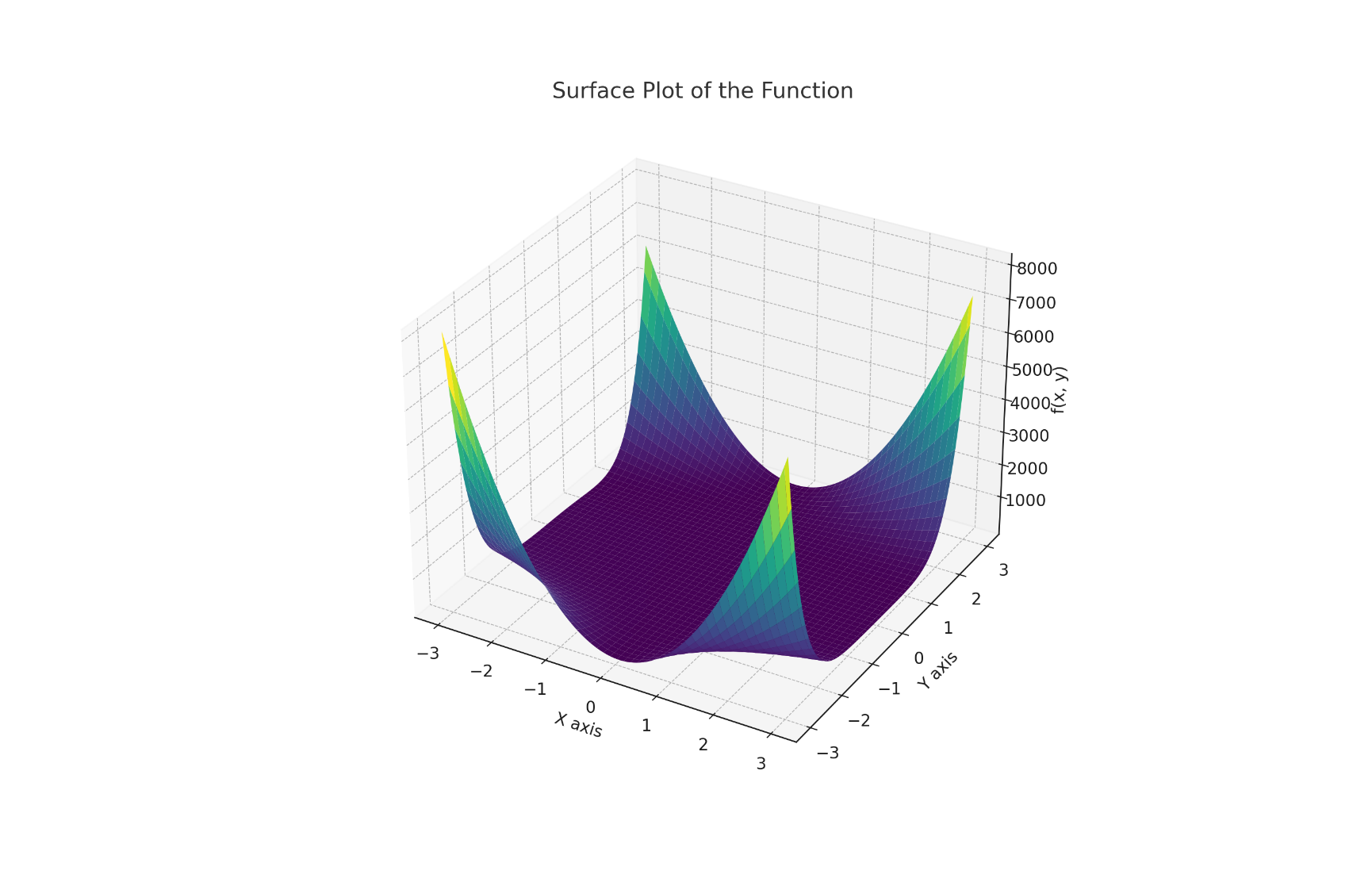
Рисунок 1.7 – График функции Розенброка

1.3 Минимум функции Швефеля

В тестовом вопросе № 3 дана функция. Необходимо составить программу, вычисляющую его глобальный минимум.

Рисунок 1.8 – Функция Швефеля

Ниже представлен результат работы программы, листинг кода находится в приложении В (рисунок 1.9).

Рисунок 1.9 – Результат работы

Также для данной функции был построен график (рисунок 1.10).

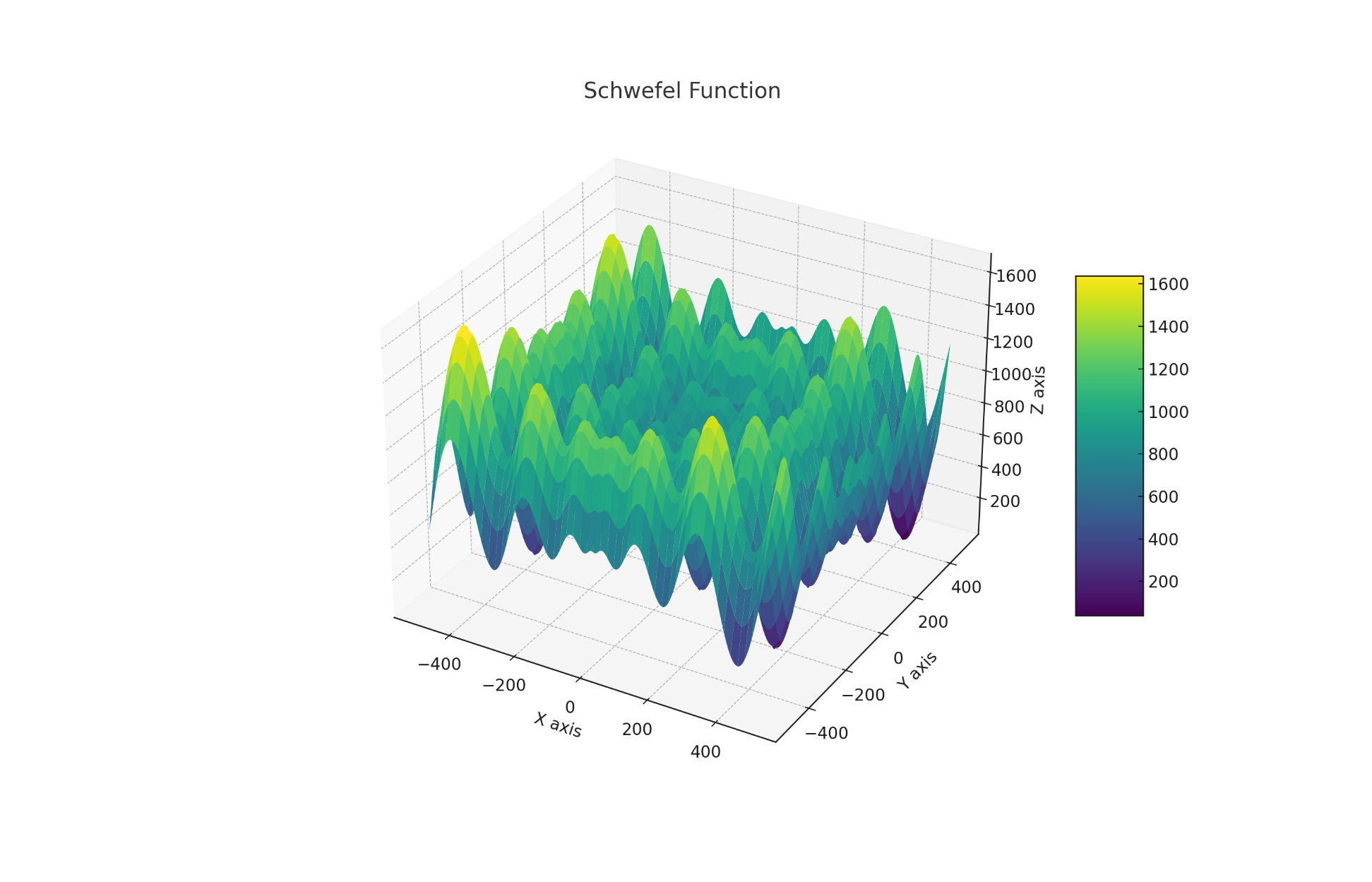
Рисунок 1.10 – График функции Швефеля

Заключение

В ходе выполнения лабораторной работы была освоена минимизация функции без ограничения на переменные, а также найден минимум функции Розенброка, глобальный минимум функции Била и глобальный минимум функции Швефеля.

Приложение А

(обязательное)

using System;

class Rosenbrock

{

static double a = 1.0;

static double b = 100.0;

static double Function(double x, double y)

{

return Math.Pow(a - x, 2) + b * Math.Pow(y - Math.Pow(x, 2), 2);

}

static void Main()

{

double x = -1.0; // Начальное значение x

double y = 1.0; // Начальное значение y

double learningRate = 0.001; // Шаг обучения

int maxIterations = 10000; // Максимальное количество итераций

for (int i = 0; i < maxIterations; i++)

{

// Вычисляем производные

double derX = -2 * (a - x) - 4 * b * x * (y - Math.Pow(x, 2));

double derY = 2 * b * (y - Math.Pow(x, 2));

// Обновляем значения x и y

x -= learningRate * derX;

y -= learningRate * derY;

// Проверяем условие сходимости (опционально)

if (Math.Abs(derX) < 1e-6 && Math.Abs(derY) < 1e-6)

break;

}

Console.WriteLine($"Минимум достигается в точке: x = {x:F2}, y = {y:F2}");

Console.WriteLine($"Значение функции в минимуме: {Function(x, y):F2}");

}

}

Приложение Б

(обязательное)

using System;

using System.Numerics;

using MathNet.Numerics;

using MathNet.Numerics.Optimization;

class Program

{

static void Main()

{

// Определение функции, минимум которой нужно найти

Func<Vector<double>, double> f = v =>

{

double x = v[0];

double y = v[1];

return Math.Pow((1.5 - x + x * y), 2) + Math.Pow((2.25 - x + x * Math.Pow(y, 2)), 2) + Math.Pow((2.625 - x + x * Math.Pow(y, 3)), 2);

};

// Создание целевой функции

var objective = ObjectiveFunction.Value(f);

// Задание начального приближения

var initialGuess = new double[] { 0.0, 0.0 };

// Создание оптимизатора (метод L-BFGS-B)

var optimizer = new BfgsBMinimizer(1e-5, 1e-5, 1e-5, 100);

// Поиск минимума

var result = optimizer.FindMinimum(objective, initialGuess);

// Вывод результата

Console.WriteLine("Минимальное значение y: " + Math.Round(result.MinimizingPoint[1], 2));

}

}

Приложение В

(обязательное)

using System;

class Program

{

// Определение функции Швефеля

static double Schwefel(double x, double y)

{

return 837.9658 - x * Math.Sin(Math.Sqrt(Math.Abs(x))) - y * Math.Sin(Math.Sqrt(Math.Abs(y)));

}

// Простой алгоритм градиентного спуска для нахождения минимума

static double[] GradientDescent(Func<double, double, double> function, double[] startPoint, double learningRate, int iterations)

{

double[] point = (double[])startPoint.Clone();

for (int i = 0; i < iterations; i++)

{

double gradX = (function(point[0] + 0.01, point[1]) - function(point[0], point[1])) / 0.01;

double gradY = (function(point[0], point[1] + 0.01) - function(point[0], point[1])) / 0.01;

point[0] -= learningRate * gradX;

point[1] -= learningRate * gradY;

}

return point;

}

static void Main(string[] args)

{

double learningRate = 0.001;

int iterations = 100000;

double[] startPoint = { 420, 420 }; // Начальная точка около типичного максимума для функции Швефеля

double[] minimum = GradientDescent(Schwefel, startPoint, learningRate, iterations);

Console.WriteLine($"Минимум найден в точке x: {minimum[0]}, y: {minimum[1]}");

Console.WriteLine($"Значение функции в минимуме: {Schwefel(minimum[0], minimum[1])}");

}

}