Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОННИКИ (ТУСУР)

Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)

ПОИСК ОПТИМУМА МНОГОМЕРНОЙ ФУНКЦИИ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ

Отчет по лабораторной работе №1

по дисциплине «Методы оптимизации»

Студент гр. 712-2 ___________ Л.С. Болтушкин ___________

Руководитель Старший преподаватель

_______ __________ Е.С. Катаева

__________

Томск 2023

Введение

Целью данной работы является освоение таких методов оптимизации, как симплекс метод для задачи линейного программирования, метод Франк-Вульфа для задачи нелинейного программирования, метод ветвей и границ для задачи дискретного программирования и метод уступок для задачи многокритериальной оптимизации.

1 Ход работы

1.1 Симплекс-метод

Текст и формулировка задачи представлены на рисунке 1.1.

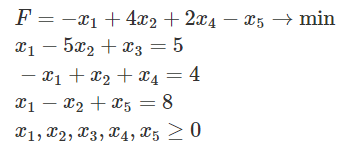
Рисунок 1.1 – Индивидуальный вариант ЗЛП

Листинг программы представлен в приложении А. Результаты работы кода представлены на рисунке 1.2.

Рисунок 1.2 – Результаты работы программного кода

1.2 Метод Франк-Вульфа

Текст и формулировка задачи представлены на рисунке 1.3.

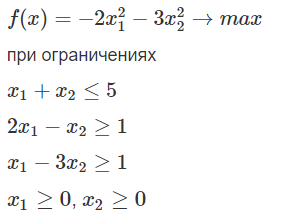
Рисунок 1.3 – Индивидуальный вариант задачи

Листинг программы представлен в приложении Б. Результаты работы кода представлены на рисунке 1.4.

Рисунок 1.4 – Результаты работы программного кода

1.3 Метод ветвей и границ

Текст и формулировка задачи представлены на рисунке 1.5.

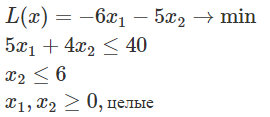
Рисунок 1.5 – Индивидуальный вариант задачи

Листинг программы представлен в приложении В. Результаты работы кода представлены на рисунке 1.6.

Рисунок 1.6 – Результаты работы программного кода

1.4 Метод ветвей и границ

Текст и формулировка задачи представлены на рисунке 1.7.

Рисунок 1.7 – Индивидуальный вариант задачи

Листинг программы представлен в приложении Г. Результаты работы кода представлены на рисунке 1.8.

Рисунок 1.8 – Результаты работы программного кода

Заключение

В ходе данной лабораторной работы были приобретены навыки работы с методом оптимизации. Также была получена информация о том, что результаты выполнения методов ручным и программным способами могут кардинально различаться при использовании готовых библиотек определенного языка программирования.

Приложение А

(обязательное)

from scipy.optimize import linprog # Коэффициенты целевой функции (минимизация) c = [-1, 4, 2, 0, -5] # Матрица коэффициентов левой части ограничений A = [ [1, -5, 1, 0, 0], [-1, 1, 0, 1, 0], [1, -1, 0, 0, 1] ] # Правая часть ограничений b = [5, 4, 8] # Задаем границы переменных (x1, x2, x3, x4, x5) x_bounds = (0, None) # Решаем задачу линейного программирования result = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds] * 5, method='highs') # Выводим результаты print('Оптимальные значения переменных:') for i, x in enumerate(result.x, start=1): print(f'x{i} = {x}') print('\nМинимальное значение целевой функции:', result.fun)

Приложение Б

(обязательное)

# Определение целевой функции def objective(x): return -2*x[0]**2 - 3*x[1]**2 # Определение ограничений def constraint1(x): return x[0] + x[1] - 5 def constraint2(x): return 2*x[0] - x[1] - 1 def constraint3(x): return x[0] - 3*x[1] - 1 # Перебор значений x в допустимом диапазоне max_value = -float('inf') solution = (0, 0) for x1 in range(6): # предполагая, что x1 не может быть больше 5 for x2 in range(6): # предполагая, что x2 не может быть больше 5 x = [x1, x2] if constraint1(x) >= 0 and constraint2(x) >= 0 and constraint3(x) >= 0: current_value = objective(x) if current_value > max_value: max_value = current_value solution = (x1, x2) # Вывод результата print(f'Найдено оптимальное решение: x1 = {solution[0]}, x2 = {solution[1]}, максимальное значение функции = {max_value}')

Приложение В

(обязательное)

# Функция для проверки выполнения ограничений def is_feasible(x1, x2): return 5*x1 + 4*x2 <= 40 and x2 <= 6 # Функция для вычисления значения целевой функции def objective(x1, x2): return -6*x1 - 5*x2 # Перебор всех возможных комбинаций x1 и x2 optimal_x1 = 0 optimal_x2 = 0 optimal_value = float('inf') # Инициализация максимально возможным значением # Верхняя граница для x1, когда x2 равно 0 x1_upper_bound = 40 // 5 # Перебор всех возможных комбинаций x1 и x2 for x1 in range(x1_upper_bound + 1): for x2 in range(7): # x2 варьируется от 0 до 6 включительно if is_feasible(x1, x2): current_value = objective(x1, x2) if current_value < optimal_value: optimal_value = current_value optimal_x1 = x1 optimal_x2 = x2 # Вывод результата print("Оптимальные значения переменных:") print(f"x1 = {optimal_x1}") print(f"x2 = {optimal_x2}") print("\nМинимальное значение целевой функции:") print(f"L(x) = {optimal_value}")

Приложение Г

(обязательное)

# Определяем функции целевых функций и ограничений def f1(x1, x2): return 5 * x1 + 3 * x2 def f2(x1, x2): return 2 * x1 + 3 * x2 def constraint1(x1, x2): return 2 * x1 + x2 <= 10 def constraint2(x1, x2): return x1 + 3 * x2 <= 12 # Находим оптимальное решение для f1 max_f1 = None max_f1_value = -float('inf') for x1 in range(11): for x2 in range(5): if constraint1(x1, x2) and constraint2(x1, x2): current_f1_value = f1(x1, x2) if current_f1_value > max_f1_value: max_f1_value = current_f1_value max_f1 = (x1, x2) # Находим оптимальное решение для f2, учитывая уступку min_f2 = None min_f2_value = float('inf') delta1 = 0.5 for x1 in range(11): for x2 in range(5): if constraint1(x1, x2) and constraint2(x1, x2) and f1(x1, x2) >= max_f1_value - delta1: current_f2_value = f2(x1, x2) if current_f2_value < min_f2_value: min_f2_value = current_f2_value min_f2 = (x1, x2) # Выводим результаты print(f'Оптимальные значения для максимизации f1: x1={max_f1[0]}, x2={max_f1[1]}, f1={max_f1_value}') print(f'Оптимальные значения для минимизации f2 с уступкой: x1={min_f2[0]}, x2={min_f2[1]}, f2={min_f2_value}')