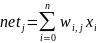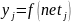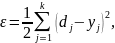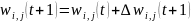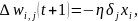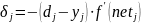Лабораторная_работа_№_2

Ордена Трудового Красного Знамени

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

Московский технический университет связи и информатики

Лабораторная работа №2

Выполнил:

________________________

подпись дата

Проверил:

________________________

подпись дата

Обучение однослойного персептрона методом стохастического градиентного спуска

Цель работы. Изучить алгоритм обучения однослойного персептрона методом стохастического градиентного спуска.

Задание. Построить и обучить нейронную сеть для распознавания цифровых рукописных символов из базы данных MNIST (Mixed National Institute of Standards and Technology database). Нейронная сеть должна корректно распознавать образы из тестовой выборки в большинстве случаев. Общий процент ошибки распознавания образов не должен быть выше 20%.

Теоретические сведения.

Алгоритм обучения методом стохастического градиентного спуска

Шаг 1. Подготовить обучающую выборку, каждый элемент которой будет состоять из пар (X, D)_m (m=1,…q) – обучающего вектора X = (x₁,…,x_n) (i=1,…,n) с вектором желаемых значений D = (d₁,…,d_k) (j=1,…,k) выходов персептрона.

Шаг 2. Генератором случайных чисел всем синаптическим весам w_i,j и нейронным смещениям w_0,j (i=1,…,n; j=1,…,k) присваиваются некоторые малые случайные значения.

Шаг 3. Из обучающей выборки (X, D)₁,…,(X, D)_q, случайным образом взять пару (X, D)_m.

Шаг 4. Из этой выбранной пары (X, D)_m взять вектор X_т = (x₁,…,x_n) и подать его на входы персептрона x₁,…,x_n. Сигналам нейронных входов смещения x₀ присваиваются единичные значения: x₀ = 1.

Шаг 5. Для каждого j-го нейрона вычислить взвешенную сумму входных сигналов net_j и выходной сигнал y_j на основании функции активации f:

Шаг 6. Вычислить ошибку ε для текущего обучающего вектора ε:

где d_j – желаемое, а y_j - фактическое значение выхода j-го нейрона в соответствии с поданным m-ым входным вектором X_m из пары (X, D)_m, k – количество выходов (классов) персептрона.

Шаг 7. Проверить критерий останова обучения, если он выполняется, то завершить обучение. В противном случае переход к следующему шагу.

Шаг 8. Произвести коррекцию синаптических весов j-го нейрона и нейронных смещений:

где t – номер итерации, η – коэффициент скорости обучения.

Шаги 5-8 выполняются последовательно для каждого входного образа, на котором обучается персептрон.

Шаги 5 и 8 повторяются для всех нейронов персептронного слоя при подаче конкретного образа.

Критерии останова алгоритма обучения могут быть следующими:

1. Значение ошибки ε для текущего обучающего вектора, вычисляемое на текущем случайно взятом обучающем векторе не превышает заданного заранее установленного порогового значения ε_порог, близкого к нулю: .

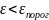2. Превышен установленный лимит количества эпох.

3. Значение общей ошибки всей сети меняется незначительно на протяжении нескольких эпох.

Указанные критерии останова обучения используются как по отдельности, так и вместе. Важным замечанием будет то, что использование только 2-го и 3-го критерий могут привести к недообучению сети, поэтому их использование без комбинации с 1-ым критерием, не рекомендуется.

Скорость обучения η выбирают в пределах [0.05…1.0] в зависимости от функции активации, но если скорость обучения константа, то её следует выбирать в пределах [0.0…0.01], так как при больших значениях метод градиентного спуска может расходиться и «проскакивать» области минимума, которые вычисляет антиградиент. Метод может расходиться и при таком коэффициенте скорости обучения, в зависимости от функции активации.

Ход выполнения работы

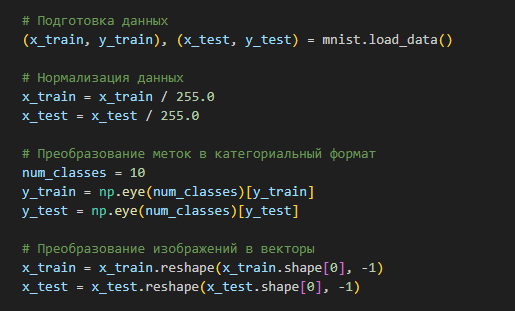
Подготовим данные для распознавания. Будем использовать базу данных MNIST, которая включает 60,000 изображений для обучения и 10,000 изображений для тестирования. Каждое изображение, имеющее размер 28x28 пикселей, представляет собой одну цифру в диапазоне от 0 до 9.

Для обеспечения более эффективной сходимости алгоритма, значения пикселей нормализованы к диапазону от 0 до 1. Кроме того, метки классов трансформируются в формат one-hot encoding, что оптимально для задач многоцелевого распознавания.

Инициализируем синаптические веса и нейронные смещения случайными значениями из диапазона [-0.01, 0.01].

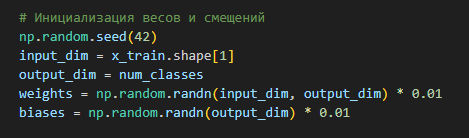
Архитектура используемой нейронной сети включает три основных слоя: входной, скрытый и выходной.

Входной слой состоит из 784 нейронов, что соответствует количеству пикселей в изображении размером 28x28, каждый пиксель преобразуется в один элемент вектора. Эти данные поступают в скрытый, где происходит дальнейшая обработка информации.

Выходной слой содержит 10 нейронов, каждый из которых предназначен для представления одной из десяти цифр от 0 до 9. Для активации нейронов выходного слоя используется сигмоидальная функция, что позволяет интерпретировать выходные данные как вероятности принадлежности входного изображения к одной из десяти категорий.

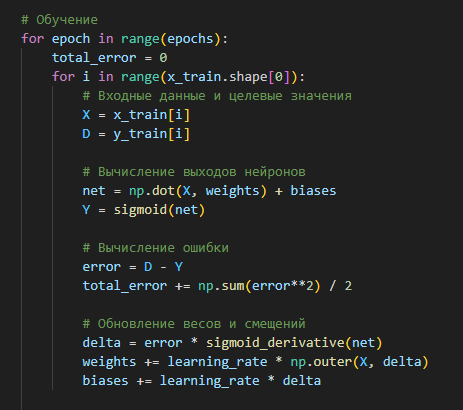
Параметры обучения:

- Скорость обучения: Установленная скорость обучения составляет 0.1, что позволяет достаточно быстро адаптировать параметры модели без риска сильных колебаний в процессе минимизации ошибки.

- Количество эпох: Процесс обучения длится 20 эпох, после чего автоматически прекращается. Это определено как критерий завершения обучения.

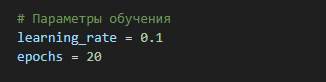
Итоговый результат обучения:

Вывод.

В лабораторной работе было изучено обучение однослойного персептрона для распознавания рукописных цифр из базы данных MNIST, применяя метод стохастического градиентного спуска (SGD). Основная цель состояла в том, чтобы доля ошибок распознавания не превышала 20%. Однако, финальная точность модели на тестовой выборке оказалась на уровне 91.6%, что соответствует лишь 8.4% ошибок. Этот результат значительно превышает установленный порог, что является признаком высокой эффективности применяемого алгоритма.

Эффективность метода стохастического градиентного спуска (SGD) проявляется через ряд преимуществ и особенностей:

1. Высокая скорость обучения: SGD отличается высокой скоростью обучения благодаря обновлению весов после каждого обучающего примера. Это позволяет быстрее сойтись к минимуму функции потерь по сравнению с методом коррекции по ошибке, где обновления происходят реже.

2. Обучение на больших наборах данных: SGD эффективно справляется с обучением на больших объемах данных, таких как в случае с базой данных MNIST. Благодаря этой особенности метод хорошо подходит для обучения моделей даже при наличии большого количества обучающих примеров.

Исходный код программы

Git:

import numpy as np

from tensorflow.keras.datasets import mnist

# Функция активации (сигмоида)

def sigmoid(x):

    return 1 / (1 + np.exp(-x))

# Производная функции активации (сигмоида)

def sigmoid_derivative(x):

    return sigmoid(x) * (1 - sigmoid(x))

# Подготовка данных

(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Нормализация данных

x_train = x_train / 255.0

x_test = x_test / 255.0

# Преобразование меток в категориальный формат

num_classes = 10

y_train = np.eye(num_classes)[y_train]

y_test = np.eye(num_classes)[y_test]

# Преобразование изображений в векторы

x_train = x_train.reshape(x_train.shape[0], -1)

x_test = x_test.reshape(x_test.shape[0], -1)

# Инициализация весов и смещений

np.random.seed(42)

input_dim = x_train.shape[1]

output_dim = num_classes

weights = np.random.randn(input_dim, output_dim) * 0.01

biases = np.random.randn(output_dim) * 0.01

# Параметры обучения

learning_rate = 0.1

epochs = 20

# Списки для хранения значений ошибок и точности

training_errors = []

test_accuracies = []

# Обучение

for epoch in range(epochs):

    total_error = 0

    for i in range(x_train.shape[0]):

        # Входные данные и целевые значения

        X = x_train[i]

        D = y_train[i]

        # Вычисление выходов нейронов

        net = np.dot(X, weights) + biases

        Y = sigmoid(net)

        # Вычисление ошибки

        error = D - Y

        total_error += np.sum(error**2) / 2

        # Обновление весов и смещений

        delta = error * sigmoid_derivative(net)

        weights += learning_rate * np.outer(X, delta)

        biases += learning_rate * delta

    # Сохранение ошибки на текущей эпохе

    training_errors.append(total_error)

    # Оценка модели на тестовых данных

    correct_predictions = 0

    for i in range(x_test.shape[0]):

        X = x_test[i]

        D = y_test[i]

        net = np.dot(X, weights) + biases

        Y = sigmoid(net)

        if np.argmax(Y) == np.argmax(D):

            correct_predictions += 1

    accuracy = correct_predictions / x_test.shape[0]

    test_accuracies.append(accuracy)

    print(f'Эпоха {epoch+1}/{epochs}, Ошибка: {total_error:.4f}, Точность: {accuracy:.4f}')

# Финальная оценка модели на тестовых данных

correct_predictions = 0

for i in range(x_test.shape[0]):

    X = x_test[i]

    D = y_test[i]

    net = np.dot(X, weights) + biases

    Y = sigmoid(net)

    if np.argmax(Y) == np.argmax(D):

        correct_predictions += 1

accuracy = correct_predictions / x_test.shape[0]

print(f'Финальная точность: {accuracy:.4f}')

10