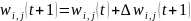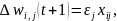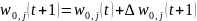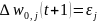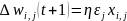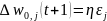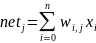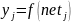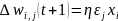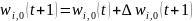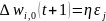Лабораторная_работа_№_1

Ордена Трудового Красного Знамени

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

Московский технический университет связи и информатики

Лабораторная работа №1

Вариант 1

Выполнил:

________________________

подпись дата

Проверил:

________________________

подпись дата

Обучение однослойного персептрона методом коррекции по ошибке через дельта-правило

Цель работы. Изучить алгоритм обучения однослойного персептрона методом коррекции по ошибке через дельта-правило.

Задание. В соответствии с вариантом, необходимо обучить нейронную сеть распознавать указанные 4 символа. На каждый символ необходимо подготовить 4 обучающих образа с использованием разных шрифтов. Соответственно, всего будет 16 обучающих образов: 4 образа первым шрифтом, 4 образа, вторым шрифтом и т.д. Тестовая выборка должна содержать по 1 образу на каждый из 4-х символов. Символы должны быть написаны другим шрифтом, который не был использован в обучающей выборке.

Теоретические сведения. Алгоритм обучения с положительным и отрицательным подкреплением можно представить в более общей форме – в виде дельта-правила. Если за d_j обозначить желаемый выходной сигнал j-го нейрона (от слов desire response, что в переводе с английского означает «желаемый отклик»), то на каждой эпохе (итерации) обучения можно рассчитывать разницу между желаемым d_j ответом j-го нейрона и реальным значением y_j, вычисляемым на его выходе. Соответственно, ошибкой выхода персептрона называется следующее выражение:

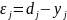
Тогда относительно алгоритма обучения персептрона с положительным и отрицательным подкреплением:

- случай ε_j = 0 соответствует шагу 4а;

- случай ε_j > 0 соответствует шагу 4б;

- случай ε_j < 0 соответствует шагу 4в.

Идея алгоритма обучения персептронного слоя с помощью правила Хебба сохранится, если итерационный процесс корректировки весов вести по формулам:

где w_i,j(t) и w_i,j(t+1) – старое и новое значения синаптических весов персептрона, Δw_i,j(t + 1) – новое значение величины коррекции синаптических весов персептрона, i – номер входного сигнала, j – номер нейрона. Приведенные формулы называются дельта-правилом.

Кроме того, можно получить аналогичную итерационную формулу для подстройки нейронного смещения b, если учесть, что его можно интерпретировать как вес w_0,j дополнительного входа x_0,j, значение которого всегда равно 1:

В итерационные формулы полезно ввести коэффициент скорости обучения η, с помощью которого можно управлять величиной коррекции синаптических весов и нейронного смещения:

При слишком больших значениях коэффициента η обычно теряется устойчивость процесса обучения, тогда как при слишком малых – увеличивается время обучения. На практике коэффициент скорости обучения η обычно задают в пределах от 0.05 до 1.

Алгоритм обучения персептрона с использованием этих формул известен под названием обучения с коррекцией по ошибке или дельта-правило.

В общем виде, алгоритм обучения с коррекцией по ошибке через дельта-правило, представлен ниже.

Алгоритм обучения методом коррекции по ошибке через дельта-правило

Шаг 1. Подготовить обучающую выборку, каждый элемент которой будет состоять из пар (X, D)_m (m=1,…q) – обучающего вектора X = (x₁,…,x_n) (i=1,…,n) с вектором желаемых значений D = (d₁,…,d_k) (j=1,…,k) выходов персептрона.

Шаг 2. Генератором случайных чисел всем синаптическим весам w_ij и нейронным смещениям w_0,j (i=1,…,n; j=1,…,k) присваиваются некоторые малые случайные значения.

Шаг 3. Из обучающей выборки (X, D)₁,…,(X, D)_q, взять следующий по счету вектор X_т = (x₁,…,x_n) и подать его на входы персептрона x₁,…,x_n. Сигналам нейронных входов смещения x₀ присваиваются единичные значения: x₀ = 1.

Шаг 4. Для каждого j-го нейрона вычислить взвешенную сумму входных сигналов net_j и выходной сигнал y_j на основании функции активации f:

Шаг 5. Для каждого j-го нейрона вычислить его ошибку:

где d_j – вектор правильных (желаемых) ответов персептрона.

Шаг 6. Произвести коррекцию синаптических весов j-го нейрона и нейронных смещений:

где t – номер итерации.

Шаги 4-6 повторяются для всех нейронов персептронного слоя при подаче конкретного образа.

Шаги 3-6 выполняются последовательно для каждого входного образа, на котором обучается персептрон.

Шаг 7. После подачи последнего обучающего вектора, проверить критерий останова обучения, если он выполняется, то завершить обучение. В противном случае – возврат к шагу 3.

Критерии останова алгоритма обучения могут быть следующими:

1. Значения синаптических весов w_i,j перестают изменяться;

2. Перестают появляться неправильные выходные сигналы y_j;

3. Превышен установленный лимит количества эпох (либо итераций).

Ход выполнения работы

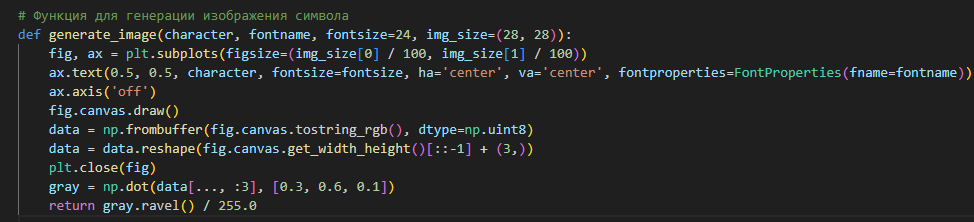
С помощью библиотеки matplotlib создадим функцию generate_image, которая принимает символ и шрифт, а затем возвращает изображение размером 28x28 пикселей в виде нормализованного массива пикселей. Эти изображения используются для обучения и тестирования персептрона.

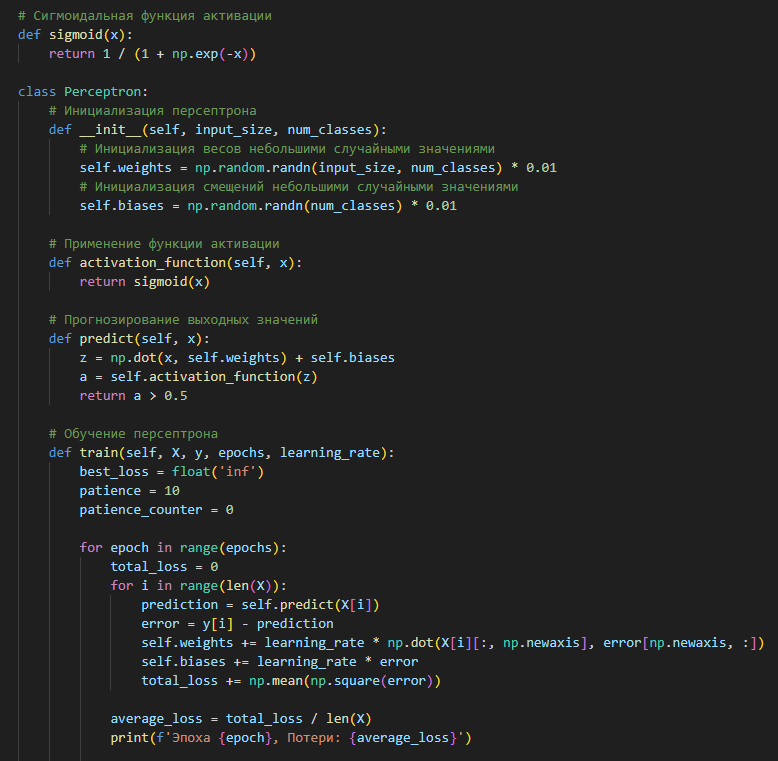
Затем инициализируем веса и смещения персептрона малыми случайными значениями. Это необходимо для обеспечения разнообразия начальных условий и предотвращения симметрии во время обучения. Веса будут инициализированы из нормального распределения с нулевым средним и стандартным отклонением 0.01, а смещения будут установлены в ноль.

Далее, используя сигмоидальную функцию активации для выходного слоя, проведем обучение персептрона методом градиентного спуска. Для коррекции весов и смещений будем использовать дельта-правило.

Параметры обучения:

- Скорость обучения: Установлена равной 0,1, что позволяет достичь быстрой сходимости без чрезмерных скачков через минимум функции потерь.

- Критерий останова: Обучение завершалось после 20 эпох, поскольку после этого количество эпох потери стабилизировались и дальнейшие итерации не улучшали результаты. Также предусмотрена функция остановки если нет улучшений на протяжении 10 эпох.

- Диапазон начальных значений весов: Веса были инициализированы случайными значениями из нормального распределения с нулевым средним и стандартным отклонением 0.01.

Итоговый результат обучения:

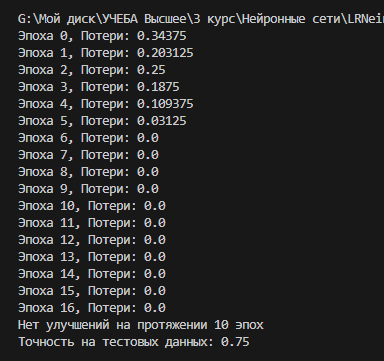
Вывод.

Однослойный персептрон, особенно когда он обучается методом коррекции по ошибке с использованием дельта-правила, демонстрирует интересные ассоциативные свойства. Он устанавливает связь между входными и выходными данными через процесс обучения, корректируя свои веса для минимизации ошибки. Благодаря этому персептрон способен достаточно точно классифицировать входные данные, даже если они содержат некоторый шум или вариации, присутствовавшие в обучающем наборе.

Во время обучения персептрон успешно минимизировал ошибку и достиг 75% точности на тестовом наборе данных. Это показывает, что модель эффективно адаптировала свои веса для распознавания символов. Однако, несмотря на высокую точность, важно учитывать несколько моментов:

- Обобщающая способность: Хотя модель показала отличные результаты на тестовом наборе, необходимо убедиться, что она также хорошо справляется с новыми данными, которые не были представлены во время обучения. Это особенно важно, если тестовый набор не полностью отражает все возможные варианты входных данных.

- Переобучение: Идеальная точность может указывать на переобучение, особенно если обучающий набор данных ограничен или не очень разнообразен. В таких случаях модель может "запоминать" обучающие примеры, а не "учиться" обобщать.

- Стабильность и устойчивость: Модель может быть чувствительна к малейшим изменениям во входных данных или инициализации весов, что может приводить к разным результатам при повторных запусках обучения.

Исходный код программы

Git:

import numpy as np

from sklearn.preprocessing import LabelBinarizer

from sklearn.metrics import accuracy_score

from matplotlib.font_manager import FontProperties

# Сигмоидальная функция активации

def sigmoid(x):

    return 1 / (1 + np.exp(-x))

class Perceptron:

    # Инициализация персептрона

    def __init__(self, input_size, num_classes):

        # Инициализация весов небольшими случайными значениями

        self.weights = np.random.randn(input_size, num_classes) * 0.01

        # Инициализация смещений небольшими случайными значениями

        self.biases = np.random.randn(num_classes) * 0.01

    # Применение функции активации

    def activation_function(self, x):

        return sigmoid(x)

    # Прогнозирование выходных значений

    def predict(self, x):

        z = np.dot(x, self.weights) + self.biases

        a = self.activation_function(z)

        return a > 0.5

   

    # Обучение персептрона

    def train(self, X, y, epochs, learning_rate):

        best_loss = float('inf')

        patience = 10

        patience_counter = 0

        for epoch in range(epochs):

            total_loss = 0

            for i in range(len(X)):

                prediction = self.predict(X[i])

                error = y[i] - prediction

                self.weights += learning_rate * np.dot(X[i][:, np.newaxis], error[np.newaxis, :])

                self.biases += learning_rate * error

                total_loss += np.mean(np.square(error))

            average_loss = total_loss / len(X)

            print(f'Эпоха {epoch}, Потери: {average_loss}')

            # Ранняя остановка, если потери не уменьшаются

            if average_loss < best_loss:

                best_loss = average_loss

                patience_counter = 0

            else:

                patience_counter += 1

                if patience_counter >= patience:

                    print(f'Нет улучшений на протяжении {patience} эпох')

                    break

# Функция для генерации изображения символа

def generate_image(character, fontname, fontsize=24, img_size=(28, 28)):

    fig, ax = plt.subplots(figsize=(img_size[0] / 100, img_size[1] / 100))

    ax.text(0.5, 0.5, character, fontsize=fontsize, ha='center', va='center', fontproperties=FontProperties(fname=fontname))

    ax.axis('off')

    fig.canvas.draw()

    data = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)

    data = data.reshape(fig.canvas.get_width_height()[::-1] + (3,))

    plt.close(fig)

    gray = np.dot(data[..., :3], [0.3, 0.6, 0.1])

    return gray.ravel() / 255.0

# Шрифты для обучения

training_fonts = [

    'LiberationSerif-Regular.ttf',

    'LiberationSerif-Bold.ttf',

    'LiberationSerif-BoldItalic.ttf',

    'LiberationSerif-Italic.ttf',

]

# Шрифт для тестирования

test_font = 'AntiquaStd-MediumItalic.ttf'

# Символы для обучения

characters = ['F', 'V', 'S', 'R']

train_data, train_labels, test_data, test_labels = [], [], [], []

label_binarizer = LabelBinarizer()

# Генерация и кодирование обучающих данных

for font in training_fonts:

    for char in characters:

        img = generate_image(char, font)

        train_data.append(img)

        train_labels.append(char)

# Генерация и кодирование тестовых данных

for char in characters:

    img = generate_image(char, test_font)

    test_data.append(img)

    test_labels.append(char)

train_data = np.array(train_data)

test_data = np.array(test_data)

train_labels_encoded = label_binarizer.fit_transform(train_labels)

test_labels_encoded = label_binarizer.transform(test_labels)

# Создание и обучение персептрона

perceptron = Perceptron(train_data.shape[1], len(characters))

perceptron.train(train_data, train_labels_encoded, epochs=20, learning_rate=0.05)

# Тестирование персептрона

predictions = perceptron.predict(test_data)

predicted_labels = label_binarizer.inverse_transform(predictions)

accuracy = accuracy_score(test_labels, predicted_labels)

print(f'Точность на тестовых данных: {accuracy}')

11