
начерт
.pdf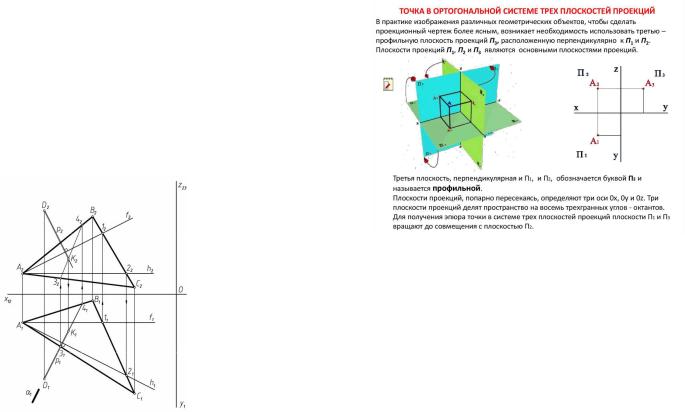
Экзаменначертательнаягеометрия |
06.07.2024г. |
называютцентром проецирования. Обычно центр проекций обозначают буквойS.
Таким образом,аппарат проецирования включает в себя: центр проецирования, проецирующие лучи и плоскость проецирования. Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пересечения этой прямой с плоскостью проекций и являетсяцентральной проекцией заданной точки на выбранной плоскости проекций.
Свойствацентральногопроецирования
1.Проекцияточкиестьточка.
2.Проекциялинииестьлиния.
3.Если точка принадлежит линии, то проекция этой точки принадлежитпроекциилинии.
4.Точка пересечения линий проецируется в точку пересечения проекцийэтихлиний.
Параллельноепроецирование.
Параллельноепроецированиеможнорассматриватькакчастныйслучай центрального проецирования, при котором центр проекций удален в бесконечность(S).
При параллельном проецировании применяют параллельные проецирующие прямые, проведенные в заданном направлении отностиельно плоскости проекций. Если направление проецирования перпендикулярно плоскости проекций, то проекции называют прямоугольными или ортогональными,востальныхслучаях-косоугольными.
При параллельном проецировании сохраняются все свойства центральногопроецирования, атакжевозникаютновыесвойства.
Параллельные проекции, как и центральные при одном центре проекций, также не обеспечивают обратимости чертежа. Применяя приемы
41
Экзаменначертательнаягеометрия |
06.07.2024г. |
Плоскостями проекций пространство делится на четыре двугранных угла — четверти. Линия пересечения плоскостей проекций называется осью координат иобозначаетсяOX.
Будем считать, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций. В связи с тем, что плоскости проекций непрозрачны, видимыми для наблюдателя будут только точки,линииифигуры,расположенныев пределах тойжепервойчетверти.
Ортогональной проекцией точки на плоскость называется основание перпендикуляра,опущенногоиз даннойточкинаэтуплоскость.
Эпюр - это проекционный чертеж, на котором плоскости проекций со всемизображеннымнанихсовмещеныопределеннымобразом
43
Экзаменначертательнаягеометрия |
06.07.2024г. |
параллельного проецирования точки и линии, можно строить параллельные проекцииповерхностиитела.
3. Основныесвойствапараллельныхпроецирования.
1.Свойство однозначности. Проекцией точки на плоскость есть
точка.
2.Свойство прямолинейности. Проекцией прямой линии на плоскостьестьпрямая.
3.Свойство принадлежности. Если точка принадлежит линии, то проекцияточкипринадлежитпроекцииэтойлинии.
4.Свойствосохранения параллельности. Проекциями параллельных прямых являютсяпараллельныепрямые.
5.Свойство деления отрезка в отношении. Если отрезок прямой линииделитсяточкойвкаком-либоотношении,тоипроекцияотрезкаделится проекциейточкивтомжеотношении.
6.Свойство параллельного переноса. Проекция фигурыне меняется припараллельномпереносеплоскостипроекций.
Три последние свойства обеспечивают более простое построение изображения и меньше искажают форму и размерыоригинала по сравнению с центральнойпроекцией.
4. Ортогональная системадвухитрехплоскостейпроекции.
ОРТОГОНАЛЬНАЯДВУХМЕРНАЯСИСТЕМАПРОЕКЦИЙ
Ортогональное проецирование состоит в смещении предмета на две взаимно перпендикулярные плоскости с помощьюлучей,перпендикулярных к этимплоскостям.
Плоскостипроекциирасполагаютсягоризонтальноивертикально.
Плоскость H называется горизонтальной плоскостью проекций, а плоскость V — фронтальной. Плоскости H и V бесконечны и непрозрачны.
42 |
|
Экзаменначертательнаягеометрия |
06.07.2024г. |
ОРТОГОНАЛЬНАЯ СИСТЕМА ТРЕХ |
ПЛОСКОСТЕЙ ПРОЕКЦИИ |
44
Экзаменначертательнаягеометрия |
06.07.2024г. |
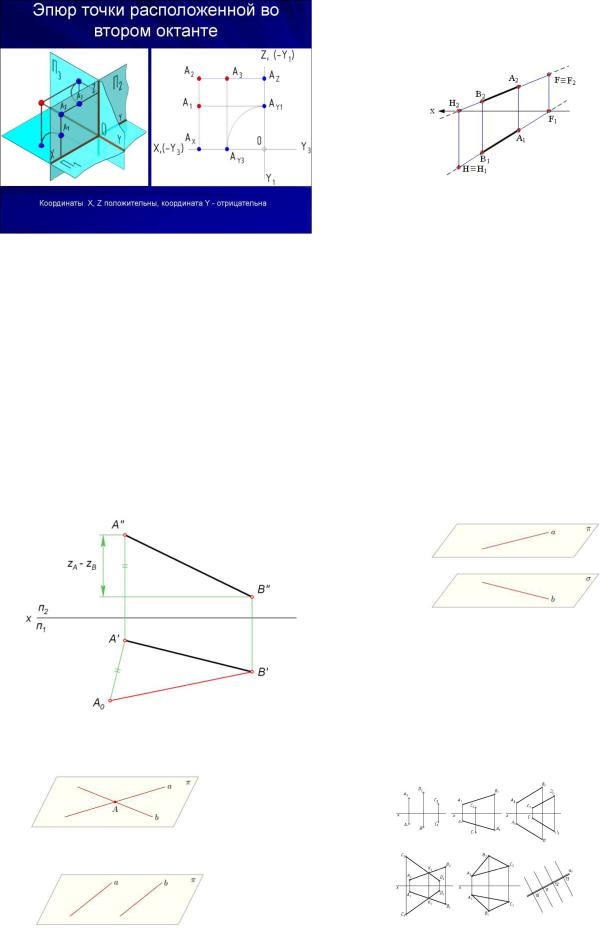
5. Эпюрточкиипрямой.
ЭПЮРТОЧКИ
6. Различныеположенияпрямойлинииотосит.п.п.
Прямая, не параллельна ни одной из плоскостей проекций, H прямойобщегоположения
Прямые параллельны или перпендикулярный плоскостям проекций, Hпрямойчастногоположения
Прямые параллельны плоскости проекции, линия уровня (прямая, параллельнаяHгоризонтальная)
Прямые, перпендикулярны п.п. – проецирующие (прямая, перпендикулярнаяH–горизонтальноипроецирующ.)
45
Экзаменначертательнаягеометрия |
06.07.2024г. |
9. Взаимноерасположениедвухпрямыхлиний.
Пересекающиеся прямые
Параллельныепрямые
Экзаменначертательнаягеометрия |
06.07.2024г. |
7.Следыпрямойлинии.
Точка пересечения прямой с плоскостями проекций. Для определениянаэпюрегоризонтальногоследапрямойнеобходимопроложить ее фронтальную проекцию до пересечения с осью Ох и в этой точке восстановить перпендикуляр до пересечения с горизонтальной проекцией прямой.
8.Определения натуральнойвеличиныотрезкапрямойлинии.
Ортогональная проекция отрезка прямой общего положения всегда меньше длинысамогоотрезка.
Методпрямоугольного треугольника
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (илифронтальной)проекцииотрезка,авеличинадругогокатетапредставляет собой разность удаления концов отрезка от горизонтальной (или, соответственно,фронтальной)плоскостипроекции.
46
Экзаменначертательнаягеометрия |
06.07.2024г. |
10.Способызадания иизображенияплоскости
1)тремяточками,нележащимина однойпрямой
2)прямойиточкой,нележащейнаэтойпрямой
3)двумя параллельнымипрямыми
4)двумяпересекающимисяпрямыми
5)плоскойфигурой
6)масштабомуклонов
Скрещивающиеся прямые (если не параллельны и не прямые, т.е. не лежат воднойплоскости)
47 |
48 |

Экзаменначертательнаягеометрия |
06.07.2024г. |
11.Плоскостиобщегоположения.Следыплоскости.
Плоскость общегоположения– этоплоскость,котораянепараллельна и не перпендикулярнаниоднойизплоскостейпроекций.
Эта плоскость произвольно наклонена к осям проекций и на эпюре ее следысоставляютскоординатнымиосямипроизвольныеуглынаклона
Положение плоскости в пространстве может быть определено ееследами.
Следплоскости-прямая,полученнаяврезультатепересечениязаданной плоскостисоднойиз плоскостейпроекций
Вобщем случае плоскость имеет три следа –горизонтальный, фронтальный и профильный, которые она образует при пересечении с известными плоскостями проекций: горизонтальнойπ1, фронтальнойπ2и профильнойπ3
Вточках аx, аy, аz, лежащих на осях координат, следы плоскости пересекаются.Этиточкиназываютсяточкамисходаследовплоскости.
49
Экзаменначертательнаягеометрия |
06.07.2024г. |
Проецирующие плоскости – плоскости, проходящие через центр проецированияиперпендикулярныекакой-либоплоскостипроекций.
Плоскость, перпендикулярная горизонтальной плоскости проекцийП1, называется горизонтально проецирующей плоскостью (рис. а). Плоскости, перпендикулярные фронтальной или профильной плоскости проекций, называютсоответственнофронтальноилипрофильнопроецирующими(рис.б ив)
Плоскости уровня – это плоскости, параллельные какой-либо плоскостипроекций.
Различают:
1)горизонтальную плоскостьуровня ׀׀П1 (рис.а);
2)фронтальнуюплоскостьуровняβ׀׀П2 (рис.б);
3)профильнуюплоскостьуровняδ׀׀П3(рис.в).
На той плоскости проекции, к которой параллельна заданная плоскость уровня, любой геометрический элемент, лежащий в ней, проецируется в натуральную величину.
51
Экзаменначертательнаягеометрия |
06.07.2024г. |
Если прямая АВ лежит в плоскости Р, то она пересечет плоскость П1 в точке М1 расположенной на линии Р1, т.е. горизонтальный след прямой, лежащейвплоскости,расположеннагоризонтальномследеплоскости.
Иными словами,следы прямой, лежащей в плоскости, расположены на одноименныхследахплоскости.Отсюдаследует,чтоследыплоскостидолжны проходитьчерезодноименныеследы прямых, лежащих вплоскости.
Чтобы построить след плоскости, необходимо определить следы двух прямых,лежащих вплоскости.
НарисункеплоскостьзаданадвумяпересекающимисяпрямымиАВиСD. Чтобы построить горизонтальный след плоскости необходимо найти горизонтальный след прямой АВ – точку М и прямой СD – точку М1. Горизонтальный след плоскости будет проходить через точки М и М1. Фронтальный след плоскости Р2 строится аналогично. Следует отметить, что для построения следа Р2 достаточно иметь фронтальный след только одной прямой,таккаквторойточкой,определяющейположениеследаР2будетточка Рх сходаследов(точка пересеченияранеепостроенного следаР1 сосьюх).
12.Плоскостичастногоположения.Их свойства.
Плоскости частного положения - плоскости, которые перпендикулярны ипараллельныплоскостямпроекций.
Плоскости частного положения обладают собирательным свойством: все геометрические образы, которые принадлежат плоскости, проецируются на плоскость проекций, которой заданная плоскость перпендикулярна, в линию, называемуюследом-проекцией.
Различают проецирующиеплоскостииплоскостиуровня
50
Экзаменначертательнаягеометрия |
06.07.2024г. |
13.Главныелинииплоскости.
Главные линии плоскостилинии уровня (горизонталь и фронталь) и линия наибольшегонаклона (линияската).
Фронтали– прямые линии, лежащие в плоскости и параллельные фронтальнойплоскостипроекций.
Горизонтали - прямые линии, лежащие в плоскости и параллельныегоризонтальнойплоскостипроекций.
Линии наибольшего наклона (ската)– прямые линии, лежащие в плоскостииперпендикулярныегоризонталиэтойплоскости.
Профильная прямая - прямая лежащая в данной плоскости и параллельная профильнойплоскостипроекций
52
Экзаменначертательнаягеометрия |
06.07.2024 г. |
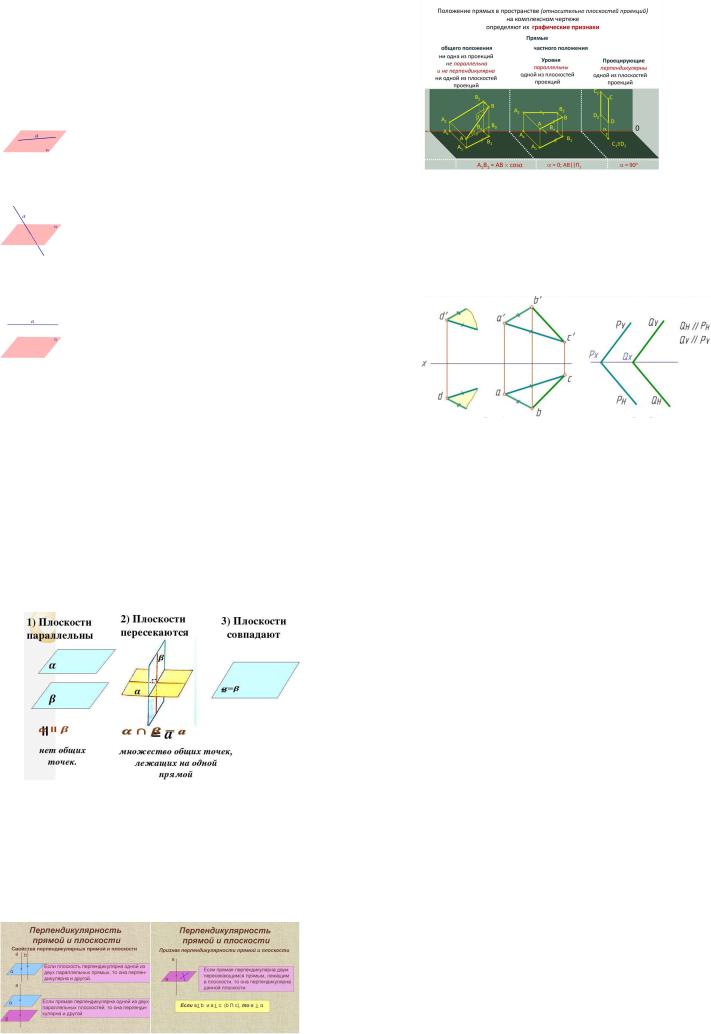
14.Различноеположенияпрямойлиниииплоскости.
Прямаялежит на плоскости(принадлежит плоскости)
Прямая лежит на плоскости, есливсе точки прямой принадлежат плоскости
(Длятого,чтобыпрямаялежаланаплоскости,необходимоидостаточно, чтобыдве любыеточкиэтойпрямойпринадлежалиэтойплоскости)
Прямаяпересекаетплоскость
Прямая пересекает плоскость, если прямая и плоскость имеютединственную общуюточку
Прямаяпараллельнаплоскости
Прямая параллельна плоскости, если прямая и плоскостьне имеют общихточек.(онинепересекаются)
53
Экзаменначертательнаягеометрия |
06.07.2024г. |
точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следуетнайтидветочки,общие дляобеихплоскостей,послечего соединитьих.
16.Перпендикулярностьпрямойиплоскости.
На плоскости прямые называют перпендикулярными, если они пересекаются под прямым углом. Главное условие перпендикулярности в пространстве то же самое — угол между прямыми или плоскостями должен быть равен 90. Если говорить о двух прямых, то перпендикулярными могут бытькакпересекающиеся,такискрещивающиесяпрямые.Перпендикулярные прямая и плоскость или две перпендикулярные плоскости обязательно будут пересекаться.
55
Экзаменначертательнаягеометрия |
06.07.2024г. |
15.Различноеположениядвухплоскостей.
Плоскостибудутпараллельными:
•если две пересекающиеся прямые одной плоскости соответственно параллельныдвумпересекающимсяпрямымдругойплоскости
•еслиплоскостипараллельны,топараллельныиходноименныеследы
Плоскостипересекаются
Результатом пересечения 2-х плоскостей является прямая. Любая прямаянаплоскостииливпространствеможетбытьоднозначнозаданадвумя
54
Экзаменначертательнаягеометрия |
06.07.2024г. |
17. Определениелиниипересечениядвух плоскостей
Линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Но положение любой прямой в пространстве определяется положением ее двух точек. Поэтому для построения линии пересечения двух плоскостей надо найти две точки, каждая из которых принадлежитобеимплоскостям.
18.Способыпреобразованияпрямой
Чтобы преобразовать прямую общего положения AB в прямую уровня, надооднуизплоскостейпроекций(например,П2)заменитьновойплоскостью проекций П4, расположив ее перпендикулярно незаменяемой плоскости проекций П1 и параллельно данной прямой AB (рис. 5.6, а). Тогда в новой системе координат П1/П4 прямая AB займет положение линии уровня относительноновойплоскостипроекцийП4.
Чтобы выполнить такое преобразование, надо новую ось координат x14 провести параллельно горизонтальной проекции A1B1 данной прямой AB (см. рис.5.6,а).Расстояниемеждуx14иA1B1выбираетсяпроизвольно.
Чтобы выполнить такое преобразование, надо новую ось координат x14 провести параллельно горизонтальной проекции A1B1 данной прямой AB (см. рис.5.6,а).Расстояниемеждуx14иA1B1выбираетсяпроизвольно.
56

Экзаменначертательнаягеометрия |
06.07.2024г. |
Экзаменначертательнаягеометрия |
06.07.2024г. |
19.Способ заменыплоскостейпроекций
Сущность этого способа заключается в том, чтозаменяют одну из плоскостей на новую плоскость, расположенную под любым утлом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степениудовлетворяющихтребованиямусловийрешаемойзадачи.
57
Экзаменначертательнаягеометрия |
06.07.2024г. |
21.Пересечениямногогранникаплоскостьючастногоположения.
Припересечениимногогранникаплоскостьючастногоположенияграни пересекаютсяпопрямымлиниям.
Линиейпересечениябудетзамкнутаяилинезамкнутаяломанаялиния.
Для построения этой линии достаточнонайти точки пересечения рёбер сзаданнойплоскостью(опорные точки)исоединитьихсучётомвидимости.
22.Пересечение поверхности вращенияплоскости общегоположения.
При пересечении поверхности вращения с плоскостью общего положенияниоднаизпроекцийлиниипересеченияневырождаетсявпрямую линию. Задача может быть решена с помощью общего способа: введение вспомогательных секущих плоскостей. Решение упрощается, если применить способ замены плоскостей проекций. Замену нужно произвести так, чтобы заданную плоскость общего положения в новой системе преобразовать в плоскость частного положения и решать задачу пересечения поверхности вращенияспроецирующейплоскостью.
Задача:Построить линию пересечения цилиндра, поверхностьФ, с плоскостью общего положенияР заданной прямыми линиямиАВ иВС (рис.7.10).
Решение: ПлоскостьР АВ ВС –общего положения, а поверхность цилиндраФ –горизонтально проецирующая, т.к. ось цилиндра перпендикулярна плоскостиН. В этом случае горизонтальная проекция искомой линии пересеченияbН совпадает с горизонтальной проекцией цилиндраФН. Для построения фронтальной проекции линии пересечения
59
20.Пересечениямногогранникаплоскостьюобщегоположения
Если многогранник пересекает плоскость общего положения, тодля определения линии пересечения необходимо воспользоваться некоторыми дополнительнымивспомогательнымипостроениями.
Этипостроенияможновыполнятьдвумяспособами:
1.Метод рёбер. Нахождение точек пересечения рёбер многогранника с плоскостью, то есть нахождение вершин многогранника, получающегосявсечении.
2.Метод граней. Нахождение линий пересечения граней многогранника ссекущейплоскостью,тоестьнахождениесторонсечения.
58
Экзаменначертательнаягеометрия |
06.07.2024г. |
удобно выполнить следующую замену плоскостей проекций: Р АВ ВС V1; проекции искомой линии пересечения на плоскостиV1 совпадает со следом плоскостиР – 1V1…2V1 . Для фронтальной проекции линии пересечения необходимопостроитьхарактерныеточки:
1 и2 –высшая инизшаяточки;
5 и6–точкивидимости;
ирядпроизвольныхточек3,4,7,8.
Рис.7.10.Линияпересеченияцилиндрасплоскостьюобщего
Положениязаданнойпрямымилиниямиавивс
Для построения фронтальных проекций точек линии пересечения осуществляют обратную заменуV1 V, при этом сохраняется высота всех точек, т.е. = 1.
60

Экзаменначертательнаягеометрия |
06.07.2024г. |
Дляпостроенияфронтальнойпроекциилюбойточки,например,точки1, необходимоиспользоватьусловие = 1 .
Полученные точки линии пересечения соединяют плавной кривой с учетомвидимости. Видима тачастьлиниипересечения,которая расположена в передней половине поверхности цилиндра, т.е. линия5V,2V,8V,4V,6V, другая частьлиниипересеченияневидима
23. Перенесение поверхности вращение плоскостью частного положения.
В зависимости от положения секущей плоскости линия пересечения с поверхностьювращенияимеетразнуюформу.
Цилиндр(прямой)
Еслисекущаяплоскостьпараллельнаоснованию,толиниейпересечения спрямымцилиндромявляется окружность. Еслиона расположенаподугломк основанию, тогда – эллипс. В случае, когда секущая плоскость перпендикулярна основанию, линияпересечения–прямоугольник.
Сфера
Линией пересечения плоскости со сферой является окружность не зависимоотположениясекущейплоскости.
Тор
Если секущая плоскость перпендикулярна оси тора, то в сечении получаем кольцо (в частном случае круг). Когда секущая плоскость расположена под иным углом к оси тора, линия пересечения представляет собой пару окружностей, эллипсов, один эллипс, либо по форме похожа на цифру«8».
Конус(прямой)
Наибольшеемногообразиепредставляютконическиесечения:
61
Экзаменначертательнаягеометрия |
06.07.2024г. |
Построим горизонтальную проекцию конуса, усеченного заданными плоскостями.
Линияпересеченияпредставляет собойна участке:
S1-отрезокпрямой;
12-дугуокружности;
23-участокпараболы;
34–участокэллипса;
34–гиперболу.
Для решения задачи достаточно построить горизонтальные проекции точек1,2,3,4,5,расположенныхнаповерхностиконуса,исоединитьихлинией. Например, проекция 11 строится так: через точку 12 проводим горизонтальную прямую до пересечения с контуром конуса в точке 62, затем радиусомS161 проводим дугу окружности и на ней по линии связи с точкой 12 находим точку 11. Аналогично строится горизонтальная проекция любой точки на поверхности конуса. Выбирая по необходимости промежуточные точки,получаемокончательноерешение.
Профильную проекцию можно построить на основании правила взаимосвязи проекций. При этом необходимо учитывать контурные точки 7,8, профильные проекции которых лежат на контуреS3A3. Поскольку участок образующейSAмеждуточками7и8вырезансекущимиплоскостями,каквидно на П2, тоинаП3 онотсутствуетмеждуточками73 и83.
Относительно осей Ф1 и Ф3 получаем симметричную картину, поэтому достаточнопостроитьпроекциинаполовине конуса.
На чертеже указываем линии пересечения секущих плоскостей, невидимыепроекциикоторых обозначеныпунктирнойпрямой.
63
Экзаменначертательнаягеометрия |
06.07.2024г. |
а) если секущая плоскость параллельна основанию конуса, тогда линия пересечения–окружность;
б) если секущая плоскость пересекает две образующих конуса, линия пересечения-эллипс;
в) когда секущая плоскость параллельна образующей, линия пересечения–парабола;
г) в случае, когда секущая плоскость пересекает одну образующую, линия пересечения–гипербола;
д) если секущая плоскость проходит через вершину конуса, в сечении имеемтреугольник.
Рассмотрим построение проекций на примере сечения прямого конуса, основание которого параллельно плоскостиП1, различно расположенными плоскостями, которые отсекают часть конуса. Как видим, на рис. 4.8 представлено все многообразие расположения секущих плоскостей. Приэтом секущие плоскости являются фронтально-проецирующими, поэтому на П2 решениеполучено.
Рис.4.8.Сечениеконуса плоскостями.
62
Экзаменначертательнаягеометрия |
06.07.2024г. |
24.Разверткамногогранников.
Разверткоймногогранника называется плоская фигура, составленнаяиз его граней, совмещенных с одной плоскостью. При этом смежными будут две грани,имеющиеобщееребро.
Все грани на развертке изображаются в натуральную величину, поэтому еепостроениесводитсякнахождениюнатуральныхвеличинотдельныхграней поверхности.
Дляпостроенияразверткипризмыприменяютдваметода:нормального сеченияираскатки.
25.Развертка цилиндраповерхности.
Боковая поверхность цилиндра представляет собой прямоугольник со сторонами Н и πD. Основания цилиндра на горизонтальной плоскости проекций изображаются в натуральную величину. Для построения развертки цилиндра (рисунок 22) нужно на свободном поле чертежа провести две параллельныепрямые,расстояниемеждунимиравновысотецилиндра –Н.
Рисунок22
На этих прямых от произвольно выбранной точки отложить расстояние, равное длине окружности – πD. Построенный прямоугольник является разверткой боковой поверхности цилиндра. Остается пристроить окружности
–основанияцилиндра.
64
Экзаменначертательнаягеометрия |
06.07.2024г. |
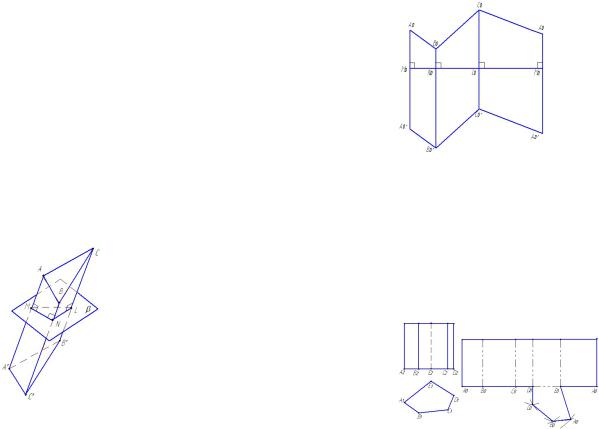
26.Построениеразвертокмногогранников(способы)
Методнормальногосечения. Нормальнымсечениемпризмыназывается ее сечение плоскостью β,перпендикулярной ребрам призмы (рис.5.4а).Такая плоскость пересекает призму по некоторому многоугольнику, в нашем случае треугольник MNL, стороны которого перпендикулярны ребрам призмы и равны расстояниям между соответствующими соседними ребрами призмы. Так АА' MN, ВВ' MN, ВВ' NL. MN, NL и LM – соответственно расстояния междуребрамиАА'иВВ',ВВ'иСС',СС'иАА'.
Дляпостроенияразверткитакойпризмысначаласледуетеенормальное сечение MNL развернуть в прямую линию М0М0 (рис. 5.4 б). Затем провести к этой прямой в точках М0, N0, L0 перпендикуляры, на которых соответственно отложитьдлиныреберотнормальногосечениядовершинпризмы:М0А0 =МА, М0А0' = МА' и т. д. Соединив полученные точки ломаными линиями, получим разверткубоковойповерхностипризмы.
Ч
Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основания призмы – треугольники АВС и А'В'С',предварительноопределив ихнатуральную величину.
а
65
Экзаменначертательнаягеометрия |
06.07.2024г. |
1.РебраоснованияпроецируютсявнатуральнуювеличинунаП1,адлину боковыхреберизмеряемнаП2.
2.Отметим в произвольном месте чертежа точку А0 на горизонтальной линии.Строим последовательно В0, С0, D0, E0, A0, переносяна эту линии длину отрезковA1B1,B1C1,C1D1,D1E1,E1A1.Врезультатераскатываемвсебоковыеграни призмы.
3.Строим на одной из сторон, например D0E0, нижнее основание, применяяметодтриангуляции.Аналогичностроимверхнееоснование.
27. Построениеразвёртки телвращения
67
Экзаменначертательнаягеометрия |
06.07.2024г. |
б
Рис. 5.4а,б
Метод раскатки.Раскатываем боковую поверхность призмы на плоскостичертежаоднуграньзадругой.
Этот способ наиболее эффективен тогда, когда основание призмы проецируетсявнатуральнуювеличинунаплоскостьпроекций.
Пример5.4. Построитьразверткупрямойпятиугольнойпризмычастного положения(рис.5.5).
Рис.5.5
66
