
начерт
.pdf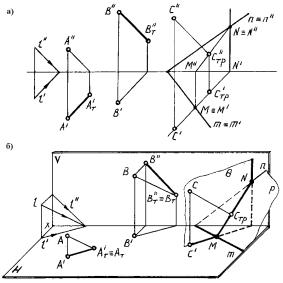
Экзаменначертательнаягеометрия |
06.07.2024г. |
|
|
|
Оглавление |
|
Стр |
|
Блок 1 |
|
3 |
1 |
Теньточки иотрезкапрямойвортогональныхпроекциях |
|
3 |
2 |
Тениплоскихфигурвортогональныхпроекциях |
|
7 |
3 |
Тенипризмыипирамидывортогональныхпроекциях |
|
8 |
4 |
Теньцилиндра иконусавортогональных проекциях |
|
10 |
5 |
Способобратноголучаприпостроениитеней |
|
12 |
|
Способлучевых сеченийприпостроениитеней.Тень отпластинынакривую |
|
|
6 |
поверхность вортогональныхпроекциях |
|
14 |
|
Способкасательныхповерхностейприпостроениитеней.Собственнаятень |
|
|
7 |
сферыивалика вортогональных проекциях |
|
15 |
|
Способвыносаприпостроениитеней.Падающаятень отсферыв |
|
|
8 |
ортогональныхпроекциях |
|
18 |
9 |
Теникарнизоввортогональныхпроекциях |
|
20 |
10 |
Теникронштейноввортогональныхпроекциях |
|
20 |
|
Тенивортогональныхпроекцияхкомбинированной(сферической– |
|
|
11 |
цилиндрической)ниши |
|
22 |
12 |
Тенивортогональныхпроекцияхсхематизированнойкапители |
|
23 |
|
Тенивортогональныхпроекцияхкомбинированной(тороидальной- |
|
|
13 |
цилиндрической)ниши |
|
25 |
14 |
Аксонометрическиепроекции.Видыаксонометрическихпроекций |
|
26 |
|
Аксонометрическиепроекции.Связь между коэффициентамиискаженияи |
|
|
|
направлениемпроецирования.Стандартныеаксонометрическиепроекции |
|
|
15 |
(ортогональныеикосоугольные) |
|
27 |
16 |
Тениваксонометрии:лестницы,цилиндрическойколоннысквадр.плитой |
28 |
|
17 |
Перспектива:определение,виды,компонентылинейнойперспективы |
29 |
|
18 |
Перспективаокружности.Перспективапараллельныхокружностей |
29 |
|
|
Выборкартины,точки зренияиугловприпостроениилинейной |
|
|
19 |
перспективы |
|
31 |
|
Видыперспективывзависимостиотположениякартиннойплоскостии |
|
|
20 |
высотыточкизрения |
|
32 |
|
Построениеперспективыспособомархитекторов(сдвумяиоднойточками |
|
|
21 |
схода) |
|
32 |
|
Методсеткивпостроенииперспективы(привестипримерспостроением |
|
|
22 |
теней) |
|
33 |
23 |
Построениетенейвперспективе |
|
35 |
|
Перспективаинтерьера (особенностивыбораточекиугловзрения). |
|
|
24 |
Привестипример |
|
37 |
|
Блок 2 |
|
40 |
1 |
Сущностьметодапроекций |
|
40 |
2 |
Центральноеипараллельноепроецирования |
|
40 |
3 |
Основныесвойствапараллельныхпроецирования |
|
42 |
|
1 |
|
|
Экзаменначертательнаягеометрия |
06.07.2024г. |
|
|
Блок1
1.Тень точкииотрезкапрямойвортогональныхпроекциях.
Падающаятень отточки
Представим себе материальную точкуА(рис.74), расположенную в пространстве над плоскостью Н, которая освещается световыми лучами, идущими из бесконечности параллельно заданному направлению. Точка А задержит один из них и отбросит теневой луч, который пересечет плоскостьН вточкеАТ'. ЭтаточкаибудетявлятьсятеньюточкиА.
Инымисловами, теньточкиявляетсяследомтеневоголуча.
Итак, чтобы построить тень, падающую от точки на какую-либо плоскостьилиповерхность,необходимочерезданнуюточкупровестипрямую, параллельную направлению лучей света, и определить точку пересечения этойпрямойсплоскостьюилиповерхностью, накоторуюпадает тень.
На рис.75а в ортогональных проекциях и на рис.75б в аксонометрии построенытени,падающиенаплоскостиН,VиP(nm)отточекА,ВиС.
Тень от точкиА падает на плоскость Нв точке АТ' (эта точка является горизонтальнымследомлучаААТ).
Тень от точкиВ падает на плоскость V в точке BТ''(эта точка является фронтальнымследомлуча АВТ).
Тень от точки в аксонометрии определяется в результате пересечения луча сеговторичнойпроекцией.
ТеньВT''(в аксонометрии) можно построить как точку пересечения луча ВВТс его фронтальной проекцией В''BT''или при помощи горизонтальной проекциилуча.
Тень от точкиСпадает на плоскость P (n m) в точке СTP(СTP',СTP”), которая определяется в результате пересечения луча ССTс заданной плоскостьюРприпомощигоризонтально-проецирующейплоскости
3
Экзаменначертательнаягеометрия |
06.07.2024г. |
|
|
4 |
Ортогональнаясистема двух итрех плоскостейпроекции |
|
42 |
5 |
Эпюрточкиипрямой |
|
45 |
6 |
Различныеположенияпрямойлинииотосит.п.п |
|
45 |
7 |
Следыпрямойлинии |
|
46 |
8 |
Определениянатуральнойвеличиныотрезка прямойлинии |
|
46 |
9 |
Взаимноерасположениедвух прямыхлиний |
|
47 |
10 |
Способызаданияиизображенияплоскости |
|
48 |
11 |
Плоскостиобщегоположения.Следыплоскости |
|
49 |
12 |
Плоскостичастногоположения.Их свойства |
|
50 |
13 |
Главныелинииплоскости |
|
52 |
14 |
Различноеположенияпрямойлиниииплоскости |
|
53 |
15 |
Различноеположениядвухплоскостей |
|
54 |
16 |
Перпендикулярностьпрямойиплоскости |
|
55 |
17 |
Определениелиниипересечениядвух плоскостей |
|
56 |
18 |
Способыпреобразованияпрямой |
|
56 |
19 |
Способызаменыплоскостейпроекций |
|
57 |
20 |
Пересечениямногогранникаплоскостью общегоположения |
|
58 |
21 |
Пересечениемногогранникаплоскостью частногоположения |
|
59 |
22 |
Пересечениеповерхностивращенияплоскостиобщегоположения |
59 |
|
23 |
Перенесениеповерхностивращениеплоскостьючастногоположения |
61 |
|
24 |
Развертка многогранников |
|
64 |
25 |
Развертка цилиндраповерхности |
|
64 |
26 |
Построениеразвертокмногогранников(способы |
|
65 |
27 |
Построениеразвёртки телвращения |
|
67 |
|
Задачи |
|
|
1 |
Построитьпересечениегеометрическихфигур |
|
|
2 |
Построитьсечениефигур плоскостью |
|
|
3Построитьпересечениеплоскостей
4 Построитьпересечениеплоскостииотрезка
5 Построитьтенивортогональныхпроекциях
6 Построитьтенивперспективе
7 Построитьтениваксонометрии
8 Построитьперспективу
9Построитьаксонометрию
2
Экзаменначертательнаягеометрия |
06.07.2024г. |
Падающаятень отпрямой линии
Тень,падающаяотпрямой линии,состоит из падающихтенейотвсехее точек.Лучи,проходящиечерезвсеточкипрямой,образуютлучевуюплоскость, атень от прямой линии есть линия пересечения лучевой плоскости с плоскостью или поверхностью, на которую падает тень (то есть след лучевой плоскости).
Тенью, падающей от прямой на плоскость, является прямая линия, поэтому для ее построения достаточно построить тени от двух точек, принадлежащихэтойпрямой.
4
Экзаменначертательнаягеометрия |
06.07.2024г. |
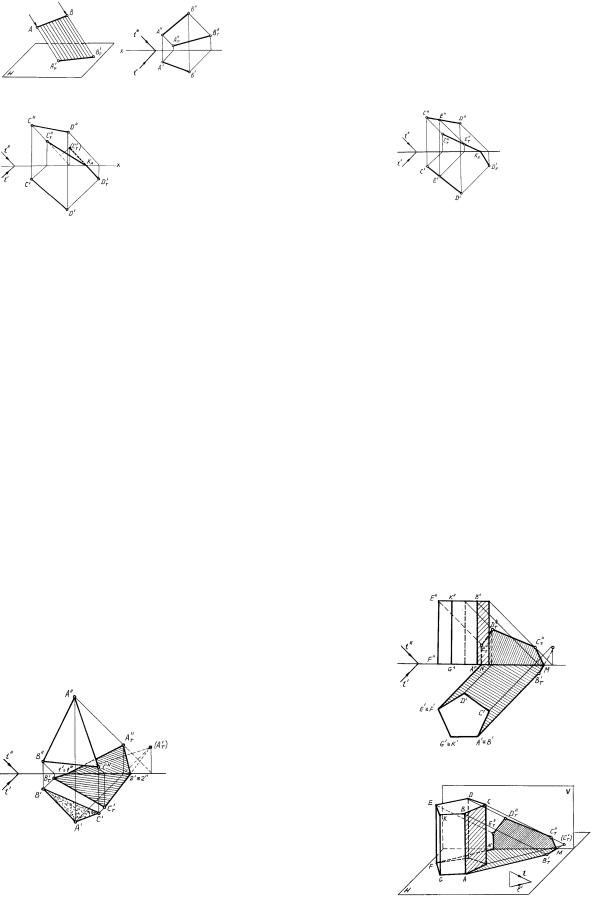
Тени от точекАиBв этом примере падают на одну плоскость проекций V, поэтому для построения тени отрезка АВ достаточно соединить между собойполученныеточкиАT''иВT''прямойлинией.
СПОСОБЫПОСТРОЕНИЯ ПРИМЕР(РИС.СМ.НИЖЕ):
Решение. Тень от отрезкаСD падает на две плоскости проекций и представляет собой ломаную линию CT''KXDT'. Точку перелома КXможно определитьдвумя способами:
5
Экзаменначертательнаягеометрия |
06.07.2024г. |
2.Тени плоскихфигурвортогональныхпроекциях.
ТЕНЬОТПЛОСКОЙФИГУРЫ(непрозрачнойпластинки)
Чтобы построить падающую тень от плоской фигуры, ограниченной многоугольником, достаточно построить тени, падающие от всех сторон многоугольника.
Нарисункепостроенатень,падающаяоттреугольникаАВСнаплоскости проекций H иV. Тень от вершины А падает на плоскость V, а от вершины В и вершины С—на плоскостьН. Следовательно, тень от стороны ВС падает на одну плоскость Ни представляет прямую линию, а тени от сторон АВ и АС падают надвеплоскостиипредставляютломаныелинии.
Экзаменначертательнаягеометрия |
06.07.2024г. |
1)припомощимнимойтени(рис.выше)
Для этого строят тень отрезка на одну из плоскостей проекций, предполагая, что второй не существует. На рисунке сначала построена тень отрезка на плоскость Н (СT'DT'). Построенная тень пересекает ось ОХв точке КX, в этой точке тень переломится и с одной плоскости перейдет на другую (в точкуСT'').
2)припомощитениотпромежуточнойточки(рис.ниже)
На чертеже точка переломаКXопределяется при помощи тени от произвольнойпромежуточнойточкиЕ(ЕT'').
6
Экзаменначертательнаягеометрия |
06.07.2024г. |
3. Тени призмыипирамидывортогональныхпроекциях.
ТЕНЬПРИЗМЫ
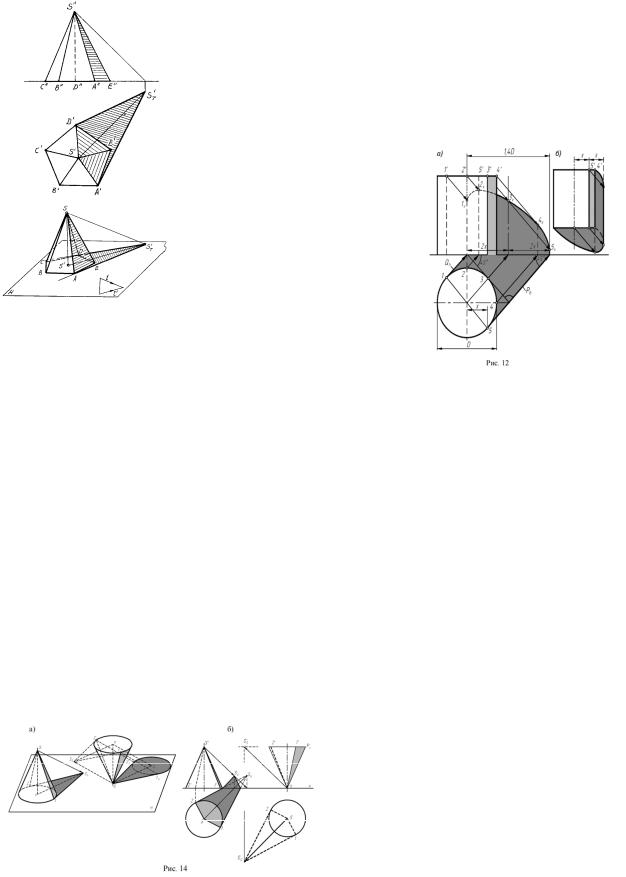
На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольнойпризмы.
Рис.89
Падающие тени от сторонАВ иАС можно построить при помощи промежуточных точек или при помощи мнимой тени (АT'), падающей от точки Аназаднюю полуплоскостьН.ПолучивтреугольникАTHВTHСTH, определяемна осиОХточкиперелома1 и2падающейтениисоединяемих сдействительной тенью АTV от точки А на плоскости V. Сторона плоской фигуры, обращенная к теневому столбу, находится в тени,тоесть у плоскихфигурследуетразличать освещенную и неосвещенную стороны. Иначе говоря, плоская фигура всегда имеетсобственнуютень.
7
Рис.90
Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на
8
Экзаменначертательнаягеометрия |
06.07.2024г. |
горизонтальнойпроекции,гдевидно,чтообращеныксветудвеграни:EFGKи KGAB.
ТЕНЬПИРАМИДЫ
Нарисунке91,92приведенпримерпостроениясобственнойипадающей тенейправильнойпятиугольнойпирамидыSABCDE.
Рис.91Рис.92
В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.
9
Экзаменначертательнаягеометрия |
06.07.2024 г. |
ТЕНЬКОНУСА.
Поверхностьконуса–этоединственнаяповерхность,дляпостроения
контура собственной тени которой надо сначала построить падающую теньнаплоскостьегооснования.
1.Через вершинуS (рис.14 а и 14б) проводится луч SSh (обратный SS0 – дляобратногоконуса).
2.Находится точка его пересечения с плоскостью основания конуса Sh
(S0).
3.ИзполученнойточкиSh(илиS0)проводятсякасательныеSh1,Sh2(S01, S02) к основанию конуса. Эти точки касания 1 и 2 определяют образующие конусаS1,S2–границусобственнойтени.
У прямого конуса в тени будет меньше половины поверхности, у обратного–большеполовины.
11
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Строим падающую теньST' от вершины S на плоскость Н и определяем падающиетениотбоковыхреберпирамиды.Линиямиконтурападающейтени пирамиды оказались прямые ST'А и ST'D.Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находитьсяграниSAE,SDEиоснование пирамиды.
4. Теньцилиндра иконусавортогональныхпроекциях.
ТЕНЬЦИЛИНДРА
Две плоскости Р и Q – касательные к цилиндру (рис. 12 а) дают собственныеипадающиетени.Теньотверхнегооснованиястроитсяпоточкам
1, 2, 3,4,5.
Падающая тень от цилиндра на стену по ширине равна 1,4 диаметра цилиндра. В точках 1v и 5v – прямые, касательные к кривой. Тень от полуцилиндрана стенкустроитсяпоразмерух(рис12б).
10
Экзаменначертательнаягеометрия |
06.07.2024 г. |
5.Способобратноголучаприпостроениитеней.
СПОСОБОБРАТНЫХЛУЧЕЙ
Способобратныхлучейприменяетсядляпостроенияпадающихтенейот одного предмета на другой. Способ основан на том, что точки пересечения теней, падающих от двух линий на плоскость, являются совпавшими тенями точекэтихлиний, лежащихнаодномсветовомлуче.
Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинкуECDF.(рисунок5.2).
Тень от проецирующей прямой SA строится методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной-идетполучевомусечению.ТеньотточкиSнапластинуESDFне надает. Для построения тени от наклонной прямой SB на пластину ESDF,
необходимо построить сначала тень падающую на плоскость 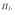 Для чего строим тень от точки S падающую на
Для чего строим тень от точки S падающую на и полученную точку
и полученную точку соединяем с точкой
соединяем с точкой т.к. точка Влежитнаплоскости
т.к. точка Влежитнаплоскости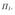
Далее строим тень от пластины ESDF на плоскость для чего строим тени точек С и D и соединяем их с точками
для чего строим тени точек С и D и соединяем их с точками лежащими на плоскости
лежащими на плоскости  Полученные тени пересекаются
Полученные тени пересекаются 
 в точке
в точке  . Из точки
. Из точки
пересечениятенейпроводимобратныйлучподуглом45°напрямую По вертикальной линии связи находим фронтальную проекцию этой точки. Обратитевнимание,чтоточки1и3,являютсяточкамиизломатенейпадающих нагоризонтальнуюплоскостьинанаклоннуюплоскостьа.
По вертикальной линии связи находим фронтальную проекцию этой точки. Обратитевнимание,чтоточки1и3,являютсяточкамиизломатенейпадающих нагоризонтальнуюплоскостьинанаклоннуюплоскостьа.
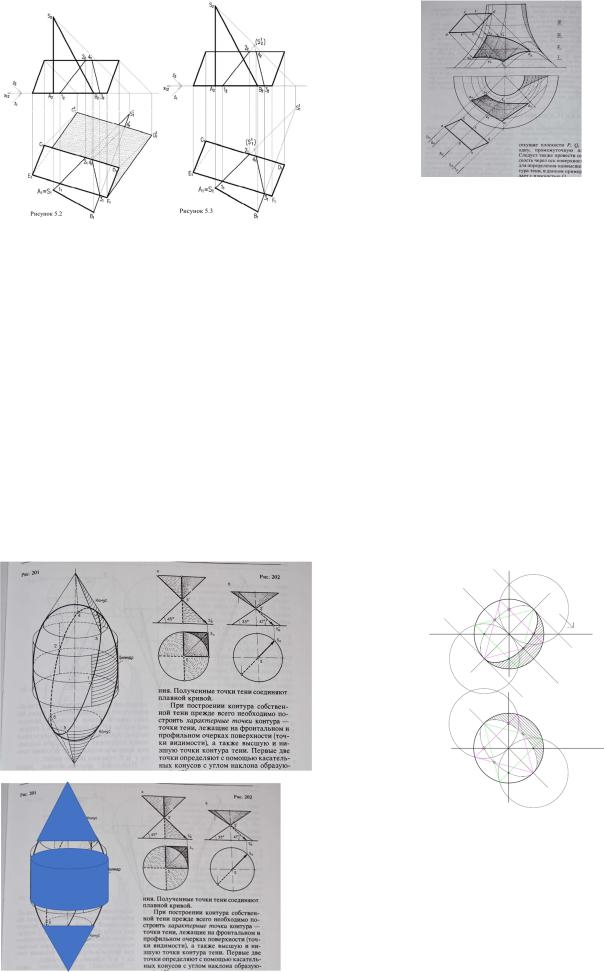
Необходимо отметить что данную задачу можно решить используя построениемнимойтениотточкиSнапластинуESDF(рисунок5.3).
12
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Экзаменначертательнаягеометрия |
06.07.2024г. |
6. Способлучевыхповерхностей
Это основной и универсальный способ построения теней. Применяется при построении падающих, а также собственных теней сложных по форме объектов.Не сложен,нотребует многографическихопераций.
Сущность – для построения падающей тени через характерные (опорные) точки объекта проводят ряд лучевых секущих плоскостей, по которым строят вспомогательные сечения. Затем определяют точки пересечения потока лучевых прямых со вспомогательными сечениями. Соединив ихопределеннымобразом,получаютконтурпадающейтени.
Построение падающей тени от плоской фигуры на поверхность вращения. Световые лучи, проходящие через контур плоской фигуры, образуют призматическую лучевую поверхность, которая при пересечении с поверхностью вращениядастконтурпадающейтени.
13
Экзаменначертательнаягеометрия |
06.07.2024 г. |
7. Способкасательныхповерхностейприпостроениитеней.
Способ вспомогательных касательных (описанных или вписанных) поверхностейконусовилицилиндровприменяетсяприпостроениинафасаде контуровсобственныхтенейповерхностейвращениябезвторойпроекции.
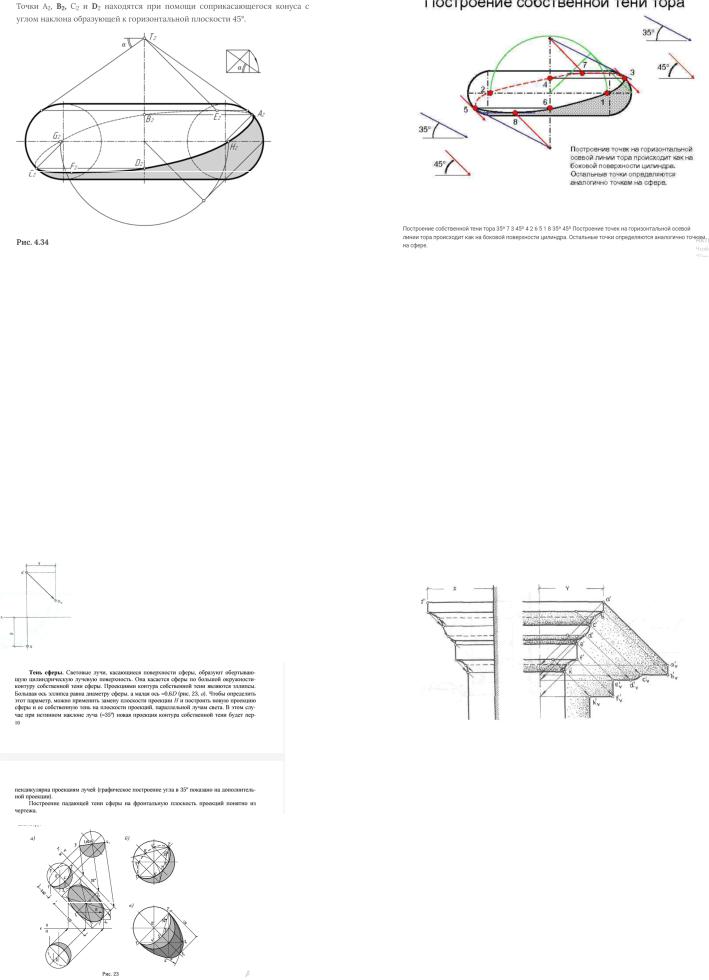
Сущность (рис. 201). Для построения точек, принадлежащих контуру собственной тени, используются вспомогательные цилиндрические или коническиеповерхности,теникоторыхопределяютсяпросто.Этиповерхности касаютсязаданнойповерхностивращенияпоокружностям–параллелям.
Нужно вычленить из сложной фигуры цилиндры и конусы. Затем построить их тени. Найти характерные точки (те что лежат на фигуре) и соединитьих.Построитьконтуртенипоэтимточкам
14
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Строим центральную ось под 90 к углу падения солнечных лучей, находим характерные точки с помощью доп построения 2х окружностей и строимтень.
Собственнаятеньсферыиваликав ортогональныхпроекциях.
15 |
16 |
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Экзаменначертательнаягеометрия |
06.07.2024 г. |
ТочкиЕ2 иF2 (самая высокая и самая низкая) строятся при помощи соприкасающегося конуса с углом наклона образующей к горизонтальной плоскостиа=35°15'52".Построение углаа показано справа вверху на рис.4.34. (построениеконусовможнопосмотретьвпредыдущемпункте)
Точки G2 и Н2 строятся при помощи соприкасающегося цилиндра вращения.
Затем все точки соединяются лекальной линией, как показано на рис.4.34.Необходимоучитывать,чтовточкахЕ2 иF2 границасобственнойтени касается параллелей тора (на фронтальной проекции - горизонтальных прямых),а вточкахА2,иС2 онакасаетсяочеркатора.
17
Экзаменначертательнаягеометрия |
06.07.2024 г. |
19
8.Способ выноса при построении теней. Падающая тень от сферы в ортогональныхпроекциях.
Способ "выноса" (ординат) применяется для построения падающих тенейнаплоскостяхпроекцийиплоскостяхуровня.
Если известно расстояние (вынос) отдельных точек объекта, например от фронтальной плоскости, падающая тень может быть построена без горизонтальнойпроекции,повыносу(ординатаму)этихточек.
Для построения тени точки Ана фронтальной плоскости проекций (рис. 208) следует от проекции точки а' отложить вправо величину выноса у и построитьвпересеченииспроекциейлучатеньavточки.
18
Экзаменначертательнаягеометрия |
06.07.2024г. |
9. Тени карнизоввортогональныхпроекциях.
Это тоже способ выноса, без горизонтальной проекции. Лучи падают по 45отоси,падающуютеньобразуютточнокоторыененаходятсявсобственной тени.
10.Тени кронштейноввортогональных проекциях
Тени кронштейнов. Форма кронштейна представляет собой цилиндрическую поверхность различного профиля, ограниченную параллельными плоскостями. Построение собственных и падающих теней кронштейна, имеющего выпуклые и вогнутые части цилиндрической поверхности, выполняют с помощью профильной проекции. Профильные проекции лучей, касательные к профилю кронштейна, определяют контуры собственной тени. Для более точного построения кривой контура падающей тенина стенуследуетизобразитьимнимые участкитени.
20

Экзаменначертательнаягеометрия |
06.07.2024 г. |
Экзаменначертательнаягеометрия |
06.07.2024г. |
11.Тени в ортогональных проекциях комбинированной (сферической – цилиндрической)ниши.
Ниши обычно имеют форму поверхностей второго порядка, поэтому падающаятень от кромки ниши на еевнутреннюю поверхностьбудет плоской кривой того же порядка (на основе теоремы Монжа о плоских сечениях). Это позволяетупроститьпостроение,выполняяегопооднойпроекции,используя опорные точки.Наклонное сечение Б-Б позволяет увидеть построение точки 6 на малой оси эллипса падающей тени. Контур собственной тени (1, 2, 3, 4, 5) построенсиспользованиемкасательныхконусов.Расстояниеотцентрасферы до точки 5 (малая полуось эллипса) равно 0,57R ≈ 0,6R. Расстояние от центра сферыдоточки6равнопримерно 1/3R,(точнееcos70o=0,342).
Полуэллипс (1 6 2) – контур падающей тени – можно построить по трем точкам. Кстати, любая точка этой кривой отстоит от линии (1 2) на 1/3 своей полухорды в направлении, параллельном малой оси эллипса. На рис. 46 построены собственная и падающая тени полуцилиндрической ниши со сферическим завершением. АВ – граница перехода, на которой лежат пограничныеточки4и7.Вточке4виденизломприпереходесобственнойтени сферы в тень цилиндра. Точка 8 – тень от точки А. Контур падающей тени не должениметьизлома,таккакповерхностицилиндра исферыкасательные.
21 |
|
|
22 |
Экзаменначертательнаягеометрия |
06.07.2024г. |
Экзаменначертательнаягеометрия |
06.07.2024г. |
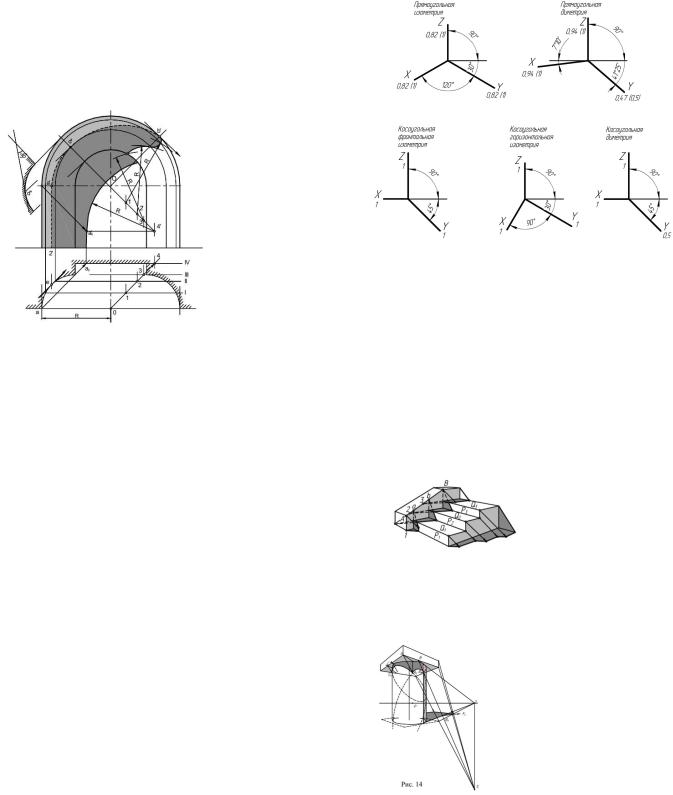
12.Тени вортогональныхпроекцияхсхематизированнойкапители
Всеэлементытенейэтогоархитектурногофрагментабылирассмотрены ранее(см. рис.210,212).
Собственная тень полувалика (эхина) построена способом касательных поверхностей. Падающаятеньотэхинанаколоннупостроенаспомощьютени на вспомогательноймеридиональнойплоскости(см.рис.233).
23 |
24 |
Экзаменначертательнаягеометрия |
06.07.2024г. |
Экзаменначертательнаягеометрия |
06.07.2024г. |
||
Точкатениа0 являетсяточкойпересеченияконтуровпадающихтенейот |
Поверхность ниши образована тороидальной и цилиндрической |
||||
двухгоризонтальныхреберквадратнойплитынастволколонны. |
поверхносятмиифронтальнойплоскостью.Собственнаятеньнишипостроена |
||||
Следует обратить внимание на четкую взаимосвязь контуров теней, а |
с помощью вспомогательного сечения, проведенного в плоскости луча (точка |
||||
d’). Для построения падающей тени от кромки ниши проведены четыре |
|||||
такженаследующие закономерности: |
|
||||
|
фронтальные плоскости посредники и построены сечения ниши этими |
||||
|
|
|
|||
1. |
точка исчезновения тени и |
точка пересечения контуров |
плоскостями.Затемнакаждойплоскостисрояттениоткромкиниши–засечки |
||
падающихтенейлежатнаодномлуче,этоточки2'и2’o,3'и 3v,4’0 и4v |
другой окружности радиуса R. Центры 1,2,3,4 вспомогательных окружностей |
||||
2. |
в точках 2', 3'и4'0 исчезновениятени, где контур падающей тени |
смещаются от проекции луча. |
В точке b’ контур падающей тени должен |
||
коснутьсякромкиниши. |
|
||||
пересекает контур собственной тени, линия контура падающей тени |
|
||||
|
|
||||
касательнак проекциилуча. |
|
14.Аксонометрическиепроекции. Видыаксонометрическихпроекций. |
|||
Падающие тени от квадратной плиты (абаки) на эхин и на колонну построены способом горизонтальных плоскостей уровня и с помощью лучевого сечения колонны фронтально проецирующей плоскостью (см. рис. 212).
13.Тени в ортогональных проекциях комбинированной (тороидальной - цилиндрической)ниши.
25
Экзаменначертательнаягеометрия |
06.07.2024г. |
восстановить положение предмета в пространстве и получить наглядное изображение.
Виды аксонометрических проекций включают прямоугольные и косоугольные проекции. Прямоугольные проекции делятся на изометрические и диметрические, а косоугольные проекции включают фронтальные диметрические, фронтальные изометрические и горизонтальныеизометрическиепроекции.
15.Аксонометрическиепроекции.Связь междукоэффициентамиискажения и направлением проецирования. Стандартные аксонометрические проекции(ортогональныеикосоугольные).
Аксонометрическая проекция — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций. При этом предмет проецируется на произвольную плоскость, которая не совпадает с его координатной плоскостью. В результате получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение предмета в пространстве и получить наглядное изображение.
Связь между коэффициентами искажения и направлением проецирования определяет тип аксонометрической проекции. Если все три коэффициента искажения равны между собой, проекция называется изометрической, если равны только два коэффициента — диметрической, а если коэффициенты неравны — триметрической. Если направление проецирования перпендикулярно плоскости проекций, проекция называется прямоугольной, а если направление проецирования не перпендикулярно плоскостипроекций—косоугольной
Аксонометрическая проекция — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций. При этом предмет проецируется на произвольную плоскость, которая не совпадает с его координатной плоскостью. В результате получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет
26
Экзаменначертательнаягеометрия |
06.07.2024г. |
16. Теньлестницы:
Построена продолжением плоскостей ступеней до пересечения с прямыми, дающими тень на эти плоскости, т.е. использован след прямой на плоскоститени
Тень цилиндрической колонны с квадратной плитой: этот пример полная аналогия построения теней в аксонометрии в перспективе. Отличие в наличии на перспективном изображении двух точек схода перспектив параллельныхреберналиниигоризонтаиточексходаперспективлучейSиих вторичныхпроекцийs
27 |
28 |

Экзаменначертательнаягеометрия |
06.07.2024г. |
17. Перспектива
Перспектива - различные способы и приёмы изображения объёмных объектовипространственныхотношенийнаплоскости.
•Виды: прямая линейная, параллельная (латеральная), обратная, усиленно сходящаяся, соединенная прямой/аксонометрической и прямой, сферическая,воздушная,панорамная,тональная
•Линейная перспектива: фронтальная, угловая, мультиточечная и перспективавтриточкисхода
18.Перспективаокружности
•Способ 1. Для получения перспективы окружности (или любой другой кривой линии) строится перспектива достаточно большого числа её точек, которые соединяются плавной кривой линией. Перспектива каждой точки строитсяприпомощидвухвспомогательныхпрямыхилидругимспособом.
•Способ 2. Около заданной окружности (или другой кривой линии) описывается квадрат (или другой многоугольник), строится перспектива квадрата или многоугольника и в него вписывается в перспективе кривая - перспективазаданнойкривой.
29
Экзаменначертательнаягеометрия |
06.07.2024г. |
19.Линейнаяперспектива
Линейная перспектива - способ изображения пространства так, как его видитчеловеческийглаз
Точказрениядолжнавыбиратьсянатакомрасстоянииотобъекта,чтобы егоможнобылолегкоохватитьодним взглядом. Горизонтальные углызрения междукрайнимилучамивпланедолжнынаходитьсявпределахот20до50°
Горизонтальный угол 50° — это предельная величина угла зрения. Лучшимиугламиследуетсчитатьуглы30 — 40°.С более близкихточекзрения рассматривать объекты целиком трудно, а на перспективных изображениях, построенных с этих точек зрения, возникают чрезмерные перспективные искажения.
31
Экзаменначертательнаягеометрия |
06.07.2024 г. |
• Перспектива параллельныхокружностей
30
Экзаменначертательнаягеометрия |
06.07.2024г. |
20.Видыперспективывзависимостиотположениякартиннойплоскостии высотыточкизрения.
Виды:
Прямая– сединойточкойсхода нагоризонте;
Обратная–сцентромсхода линийнанаблюдателе;
Панорамная – основанная на цилиндрической или сферической поверхности;
Тональная– созданная нацветеиконтрастеобъекта;
Воздушная – со снижением четкости границ при отдалении от точки зрения.
21. Построение перспективы способом архитекторов (с двумя и одной точками схода).
Исходными данными для построения перспективы является ортогональныепроекцииданногообъекта иположениелиниигоризонта.
•Построениесоднойточкойсхода(объяснение ипример)
При построении перспективы в первую очередь строиться вначале перспектива плана. Главная ось картины РР1 выбирается так, чтобы обе точки схода, по возможности, поместились в пределах чертежа. С ортогонального чертежа на основание картины в перспективе переносятся картинные следы прямых плана (точки 11,21,31), а на линию горизонта – точки схода (F1+ и F1-). Расстояния между точками в перспективе должны соответствовать их расстоянию в ортогональных проекциях или увеличены, если принимается масштабувеличения.Соединивкартинныеследы(т.1,2,3)ссоответствующими точками схода (F1+ и F1 -), получим перспективу прямых плана и контур перспективыплана.
Для построения перспективы вертикальных ребер проводятся вертикальные прямые. Ребро, проходящее через точку 21, лежит в картинной плоскости, следовательно, в перспективе оно изобразится в натуральную
32
Экзаменначертательнаягеометрия |
06.07.2024г. |
величину (с учетом масштаба при выполнении перспективы). Через верхнюю точкуребрапроводятся прямые вточкисходаF1+ иF1-.
Высота остальных вертикальных прямых определяется до точки пересечения лучей, идущих в точки схода. Эти прямые будут определять положение крайних вертикальных ребер здания в перспективе. Вершины этих реберсоединяютсясточкамисхода,ивпересеченииэтихлучейопределяется положениевершиныдальнегоребраздания.
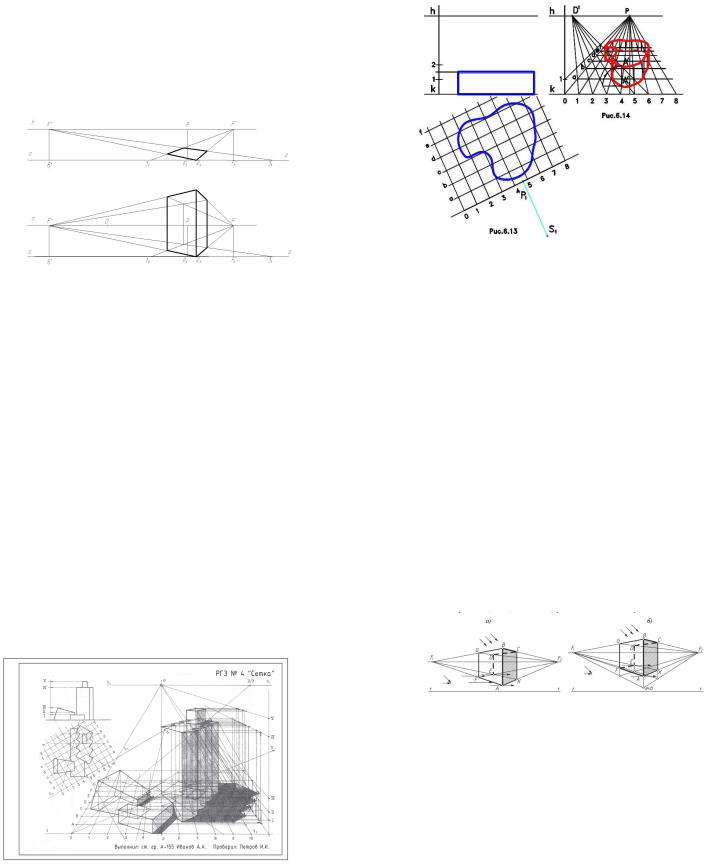
22.Метод сетки в построении перспективы (привести пример с построением теней).
Метод основан на том, что на план наносится квадратная сетка, ориентированная таким образом, чтобы одно ее направление было параллельно картине,адругое–перпендикулярно (рис.6.13).
33
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Способ перспективной сетки используется, когда сооружение имеет криволинейную форму, а также для построения планировочной перспективы, например, микрорайона. При использовании метода перспективной сетки линия горизонта должна находиться достаточно высоко («перспектива с высоты птичьего полета»), т.к. в противном случае перспективная сетка окажетсясжатойибудетнепригоднадляиспользования.
23.Построениетенейвперспективе.
При построении теней от объемных тел сначала определяется граница собственнойтени,таккакконтурпадающейтениестьтеньотконтураграницы собственной тени. Для этого мысленно проводятся перспективы и вторичные проекции лучей света. Если они пересекаются с плоскостями или прямыми, ограничивающимиих, тоэтиплоскостибудут освещаться.
Остальныеплоскостибудутнаходитьсявсобственнойтени.
На рисунке 10, апараллелепипедстоитнапредметной плоскости. Грани ABCK и CDEK находятся в собственной тени. Значит, границей собственной тенибудетломанаяABCDE.
35
Экзаменначертательнаягеометрия |
06.07.2024г. |
Размеры квадратов принимаются кратными 1, 5 или 10 м в зависимости от размеров сооружения. Вершины квадратов вдоль основания картины нумеруется цифрами, а в направлении, перпендикулярном картине, обозначаются буквами, т.е. все вершины квадратов определяется сочетанием определенного числа и буквы. На фасаде наносятся высотные отметки сооружения. Далее сетка переносится в перспективу (рис.6.14). Линии сетки, параллельные картине, строятся через деления, полученные на нулевой прямой, перпендикулярной картине, с помощью дистанционной точки D1. Линии сетки, перпендикулярные картине, сходятся в главной точке P. Затем с помощью визуального интерполирования строится перспективный план, т.е. переносятсянаглазточкисооружения,совпадающиеслиниямисетки.Высоты построенных точек откладываются также с помощью сетки. Высоту точки, взятую с фасада, измеряют по горизонтали от вторичной проекции в перспективном масштабе и откладывают затем ее по вертикали (рис.6.14, точкаA).
34
Экзаменначертательнаягеометрия |
06.07.2024 г. |
На рисунке 10, б параллелепипед расположен над предметной плоскостью. В собственной тени находятся грани ABCK, CDEK, AFEК. Значит, границейсобственнойтенибудетломанаяABCDEFА.
Рисунок10–Определениеграницысобственнойтенипараллелепипеда:
а–расположенногонапредметнойплоскости;
б–расположенногонадпредметнойплоскостью
Используя правила, рассмотренные выше,строятсятени от всех звеньев ломанойлинии.
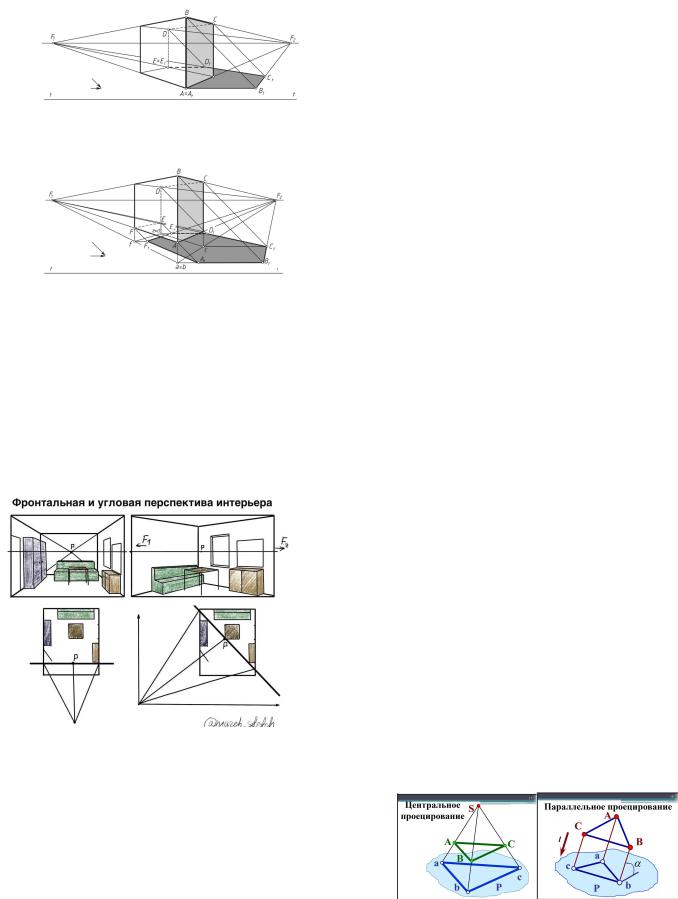
Пример 11 (рисунок 11). Построить падающую тень от параллелепипеда, расположенногонапредметнойплоскости.
ТеньототрезкапрямойАВсовпадаетсовторичнойпроекциейлучасвета (теньотвертикальногоотрезка).ОтотрезкапрямойВСтеньприпродолжении пройдет через точку схода F2 . Тень от отрезка прямой CD при продолжении пройдет через точку схода F1 . Тень от отрезка DE совпадает со вторичной проекциейлучасвета,какот любойвертикальнорасположеннойпрямой.
Пример12(рисунок12).Построитьпадающуютеньот параллелепипеда, расположенногонад предметнойплоскостью.
Для построения теней точек используется вторичная проекция параллелепипедана предметнойплоскости.
Тень отрезка АВсовпадает с вторичной проекцией световоголуча. Тень ототрезкаВСпроходитчерезточкусходаF2,ототрезкаCD–черезточкусхода F1кактениотгоризонтальныхпрямыхнагоризонтальнойплоскости.
36
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Тень от отрезка ED совпадает со вторичной проекцией луча как тень от вертикальной прямой. Тень от отрезка EF проходит через точку схода F2 , а от отрезка FA – через точку схода F1 как тени от горизонтальных прямых на горизонтальной плоскости. Соединяем теневые точки и получаем падающую теньAtBtCtDtEtFtAt.
Рисунок 11 – Построение падающей тени параллелепипеда, расположенногонапредметнойплоскости
Рисунок 12 – Построение падающей тени параллелепипеда, расположенногонадпредметнойплоскостью
24.Перспективаинтерьера(особенностивыбораточекиугловзрения).
Опытпостроенияинтерьеровпоказывает,чтонаилучшееперспективное изображение интерьера получается, если угол построения выбирать в пределах37°–53°.
37
Экзаменначертательнаягеометрия |
06.07.2024г. |
39
Экзаменначертательнаягеометрия |
06.07.2024г. |
Фронтальная перспектива отличается простотой построения и широко используетсяприпостроенииинтерьеров.
При построении композиции интерьераглавную точку картины Рможно расположить на линии горизонта различно. Если точка Р располагается в самомцентрекартины,тоизображениеназываетсяцентральнойфронтальной перспективой. Если точка Р смещается вправо или влево по линии горизонта, то изображение называется боковойфронтальной перспективой. При точке Р, сдвинутой влево, правая стена комнаты будет больше, чем левая, и наоборот, еслиточкаРсдвигаетсявправо,толеваястена будетбольшеправой.
Следовательно, в зависимости от характера композиции картины художникперемещаетглавнуюточкуРпосвоемуусмотрению.
Высота линии горизонта выбирается в соответствии с высотой глаз человекасреднегороста иобычноберется1,5,1,6или1,75м.
Дистанционная точка D в небольших помещениях выбирается на расстоянии,равномдиагоналикартины.
При построении угловой перспективы интерьера важным вопросом является компоновка чертежа и определение на картине основных ее элементов: линии горизонта hh, главной точки Р, точек отдаления F, F1 и угла зрения. Как уже говорилось, картина должна быть расположена в наилучшем полезрения, т.е.сугломзрения,равнымпримерно28–53°.
38
Экзаменначертательнаягеометрия |
06.07.2024 г. |
Блок2
1. Сущностьметодапроекций.
Метод проекций обеспечивает построение изображений пространственныхформнаплоскомчертеже.
Аппаратпроецированиявключает:
-проецирующиелучи,
-проецируемыйобъект
-плоскость,накоторойполучаетсяизображениеобъекта.
Любой материальный объект можно представить состоящим из множества точек, которые могут быть спроецированы на плоскость. В этом случаепроекцииточекформируютплоскоеизображениеобъекта.
Свойства полученных проекций во многом определяются положением центра проекцийSпоотношениюкплоскостиП´.
Приэтомразличаютцентральноеипараллельноепроецирование.
2. Центральноеипараллельноепроецирования.
Если все проецирующие лучи исходят из собственной точки (точки, находящейся в обозримом пространстве), то проецирование называется центральным, а саму точку - источник проецирующих лучей,
40
