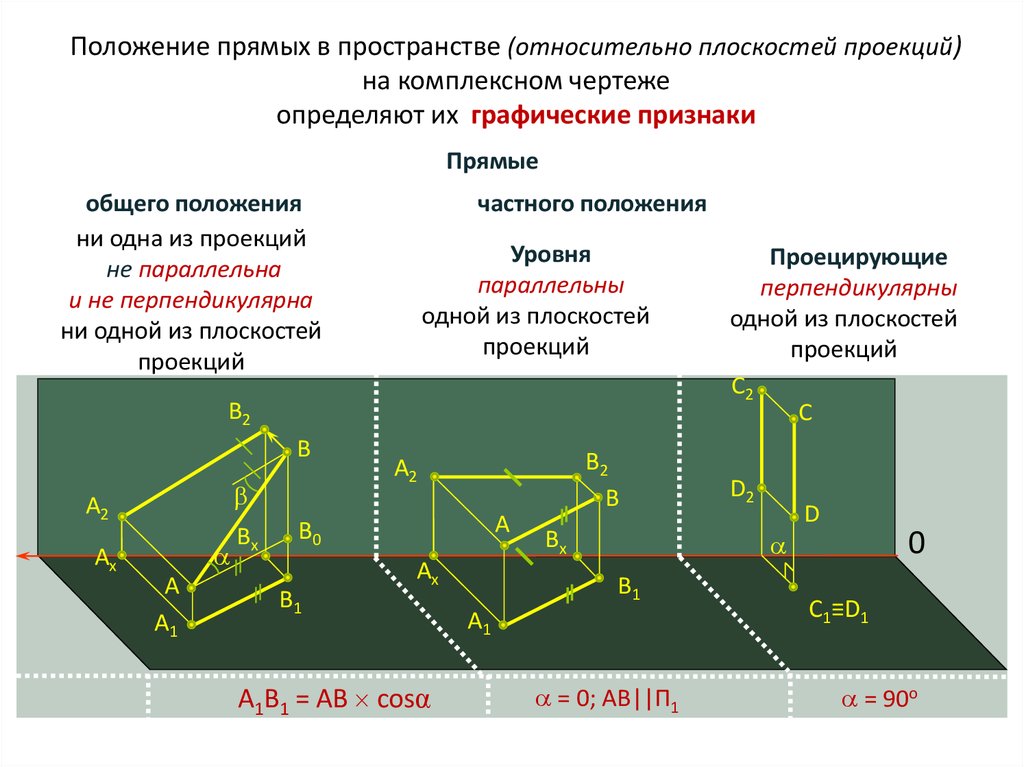
12. Плоскости частного положения. Их свойства.

Плоскости частного положения - плоскости, которые перпендикулярны и параллельны плоскостям проекций.

Плоскости частного положения обладают собирательным свойством: все геометрические образы, которые принадлежат плоскости, проецируются на плоскость проекций, которой заданная плоскость перпендикулярна, в линию, называемую следом-проекцией.

Различают проецирующие плоскости и плоскости уровня

• Проецирующие плоскости – плоскости, проходящие через центр проецирования и перпендикулярные какой-либо плоскости проекций.

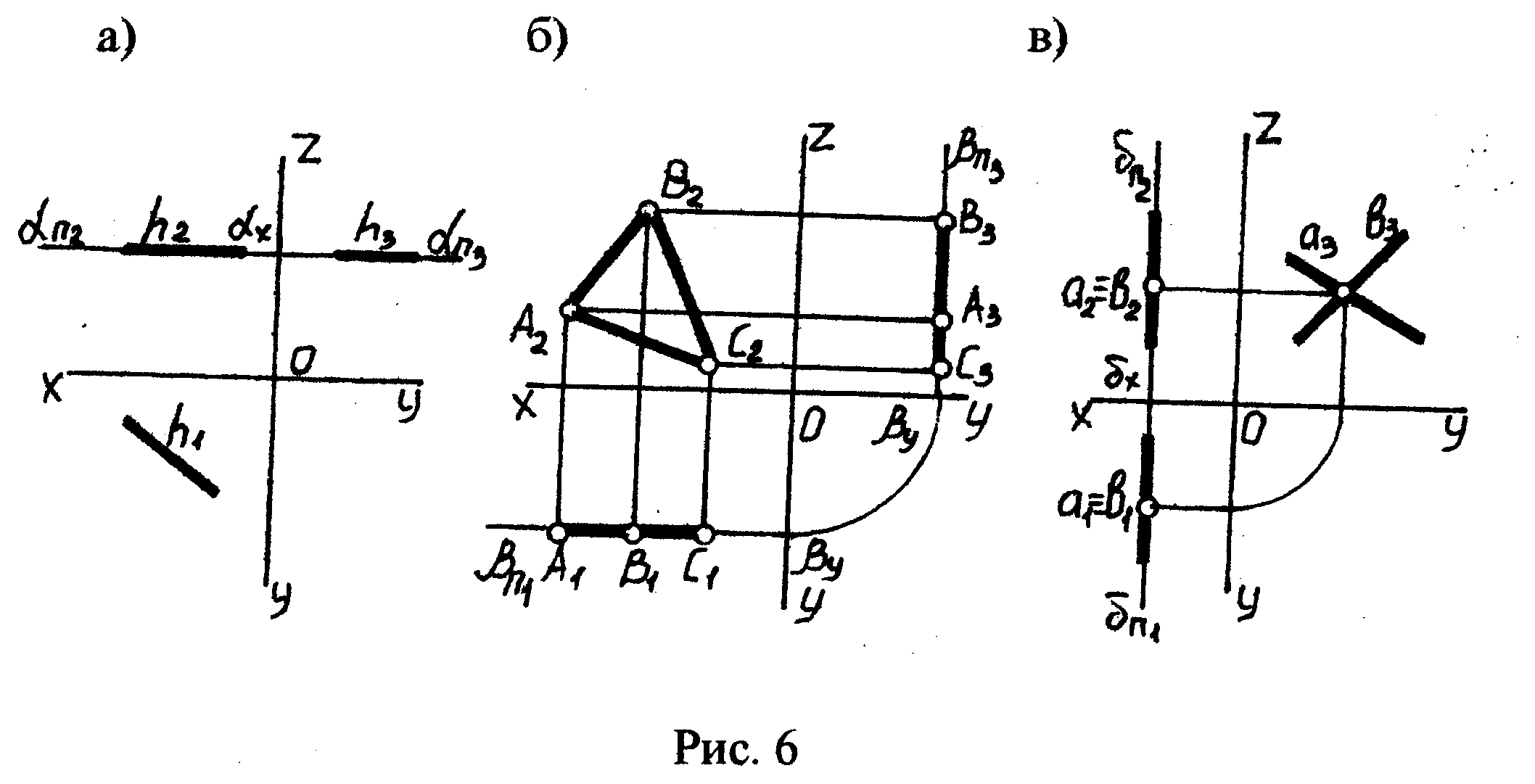
Плоскость, перпендикулярная горизонтальной плоскости проекций П₁, называется горизонтально проецирующей плоскостью (рис. а). Плоскости, перпендикулярные фронтальной или профильной плоскости проекций, называют соответственно фронтально или профильно проецирующими (рис. б и в)

• Плоскости уровня – это плоскости, параллельные какой-либо плоскости проекций.

Различают:

1) горизонтальную плоскость уровня  ׀׀ П₁ (рис.а);

2) фронтальную плоскость уровня β ׀׀П₂ (рис. б);

3) профильную плоскость уровня δ ׀׀ П₃ (рис. в).

На той плоскости проекции, к которой параллельна заданная плоскость уровня, любой геометрический элемент, лежащий в ней, проецируется в натуральную величину.

13. Главные линии плоскости.

Главные линии плоскости - линии уровня (горизонталь и фронталь) и линия наибольшего наклона (линия ската).

• Фронтали – прямые линии, лежащие в плоскости и параллельные фронтальной плоскости проекций. 

• Г 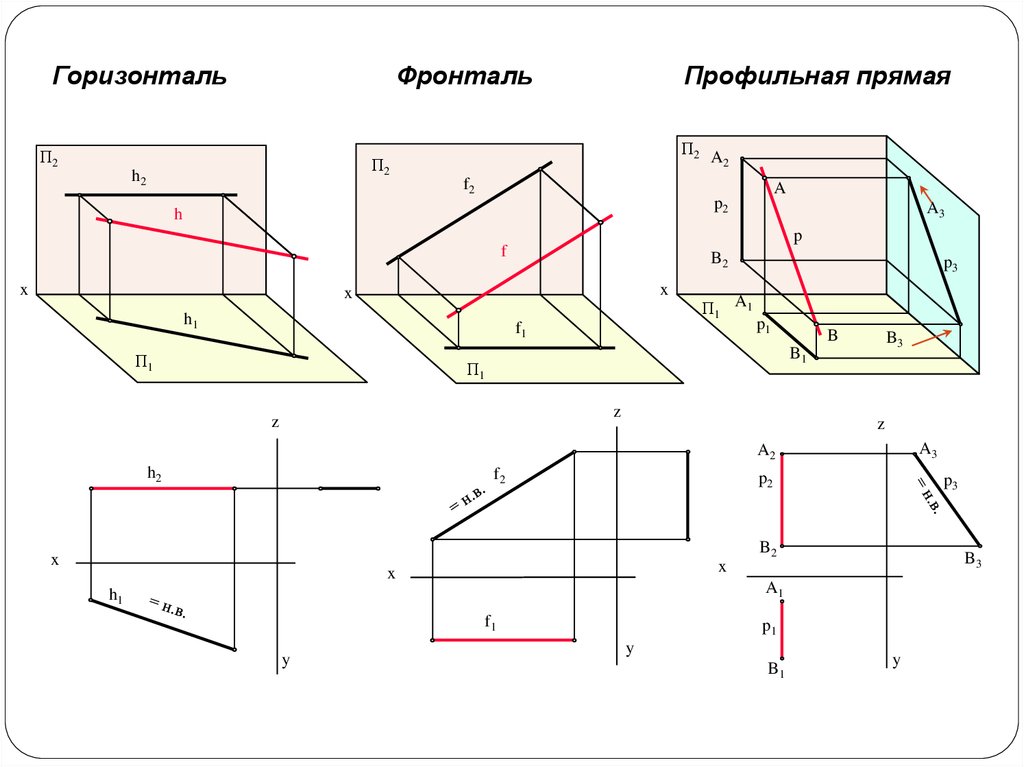оризонтали - прямые линии, лежащие в плоскости и параллельные горизонтальной плоскости проекций. 

• Л 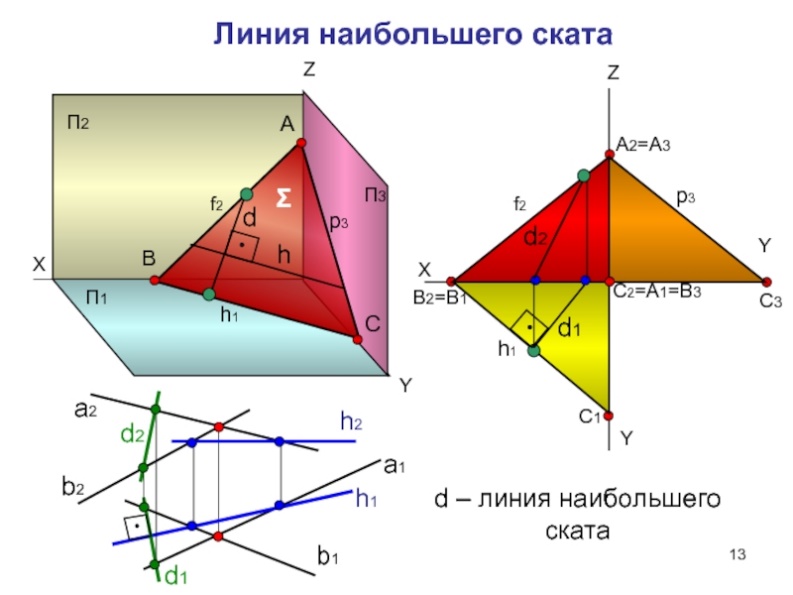инии наибольшего наклона (ската) – прямые линии, лежащие в плоскости и перпендикулярные горизонтали этой плоскости.

• Профильная прямая - прямая лежащая в данной плоскости и параллельная профильной плоскости проекций

14. Различное положения прямой линии и плоскости.

• Прямая лежит на плоскости (принадлежит плоскости)

Прямая лежит на плоскости, если все точки прямой принадлежат плоскости

(Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости)

• Прямая пересекает плоскость

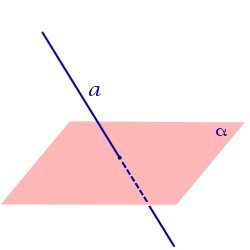Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку

• Прямая параллельна плоскости

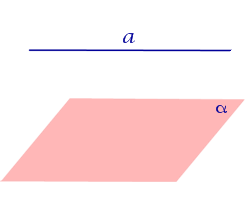Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

15. Различное положения двух плоскостей.

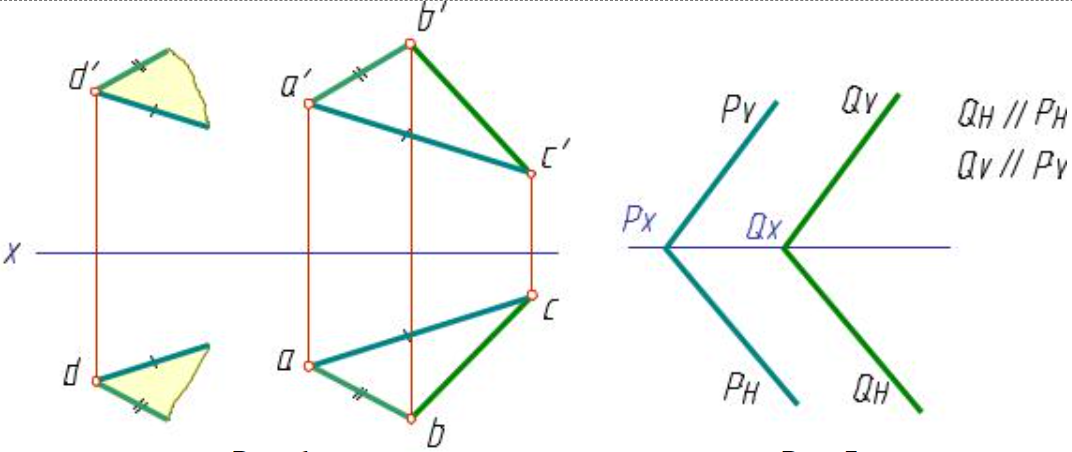
Плоскости будут параллельными:

•если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости

•если плоскости параллельны, то параллельны их одноименные следы

Плоскости пересекаются

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

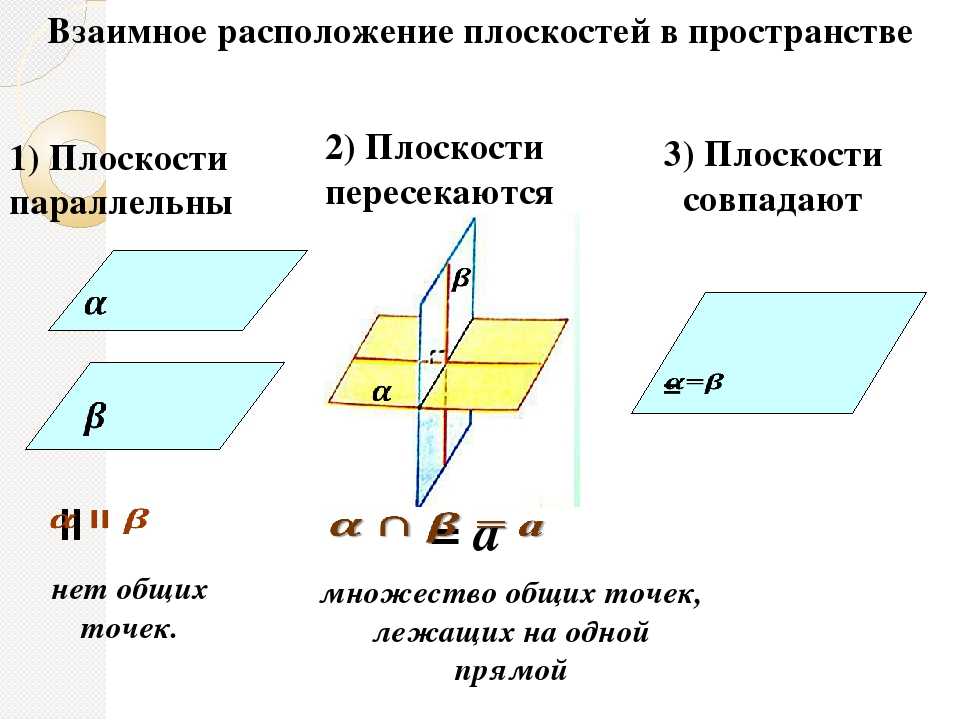
16. Перпендикулярность прямой и плоскости.

На плоскости прямые называют перпендикулярными, если они пересекаются под прямым углом. Главное условие перпендикулярности в пространстве то же самое — угол между прямыми или плоскостями должен быть равен 90. Если говорить о двух прямых, то перпендикулярными могут быть как пересекающиеся, так и скрещивающиеся прямые. Перпендикулярные прямая и плоскость или две перпендикулярные плоскости обязательно будут пересекаться.

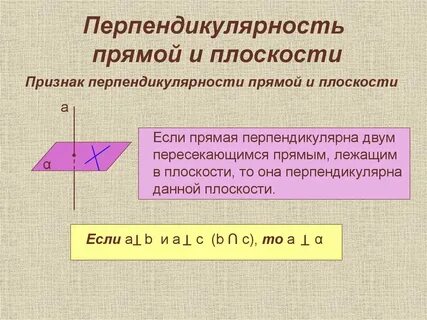
17. Определение линии пересечения двух плоскостей

Линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Но положение любой прямой в про-странстве определяется положением ее двух точек. Поэтому для построе-ния линии пересечения двух плоскостей надо найти две точки, каждая из которых принадлежит обеим плоскостям.

18. Способы преобразования прямой

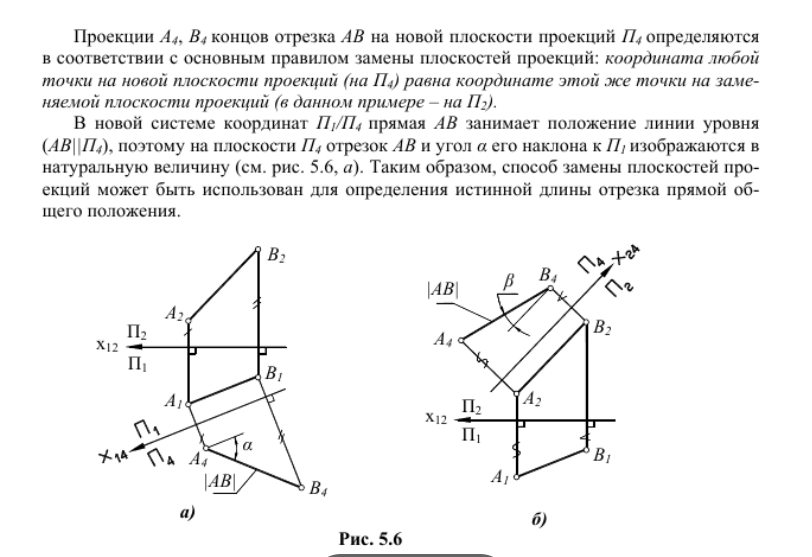
Чтобы преобразовать прямую общего положения AB в прямую уровня, надо одну из плоскостей проекций (например, П2) заменить новой плоскостью проекций П4, расположив ее перпендикулярно незаменяемой плоскости проекций П1 и параллельно данной прямой AB (рис. 5.6, а). Тогда в новой системе координат П1/П4 прямая AB займет положение линии уровня относительно новой плоскости проекций П4.

Чтобы выполнить такое преобразование, надо новую ось координат x14 провести параллельно горизонтальной проекции A1B1 данной прямой AB (см. рис. 5.6, а). Расстояние между x14 и A1B1 выбирается произвольно.

Чтобы выполнить такое преобразование, надо новую ось координат x14 провести параллельно горизонтальной проекции A1B1 данной прямой AB (см. рис. 5.6, а). Расстояние между x14 и A1B1 выбирается произвольно.

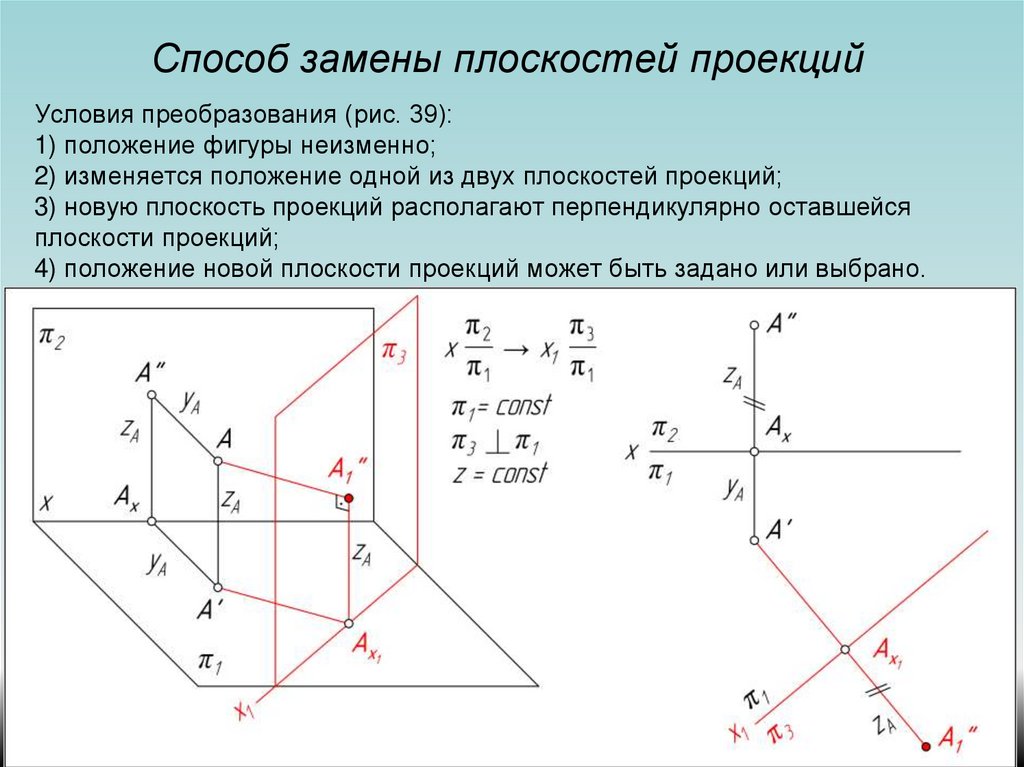
19. Способ замены плоскостей проекций

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым утлом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи.

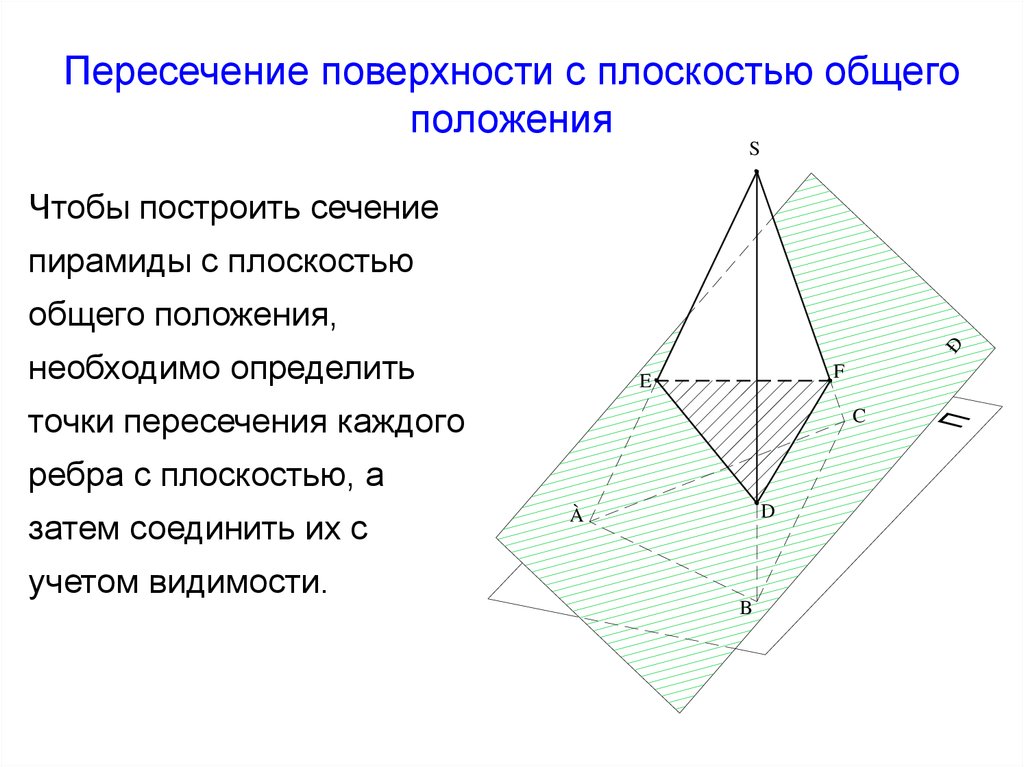
20. Пересечения многогранника плоскостью общего положения

Если многогранник пересекает плоскость общего положения, то для определения линии пересечения необходимо воспользоваться некоторыми дополнительными вспомогательными построениями.

Эти построения можно выполнять двумя способами:

1. Метод рёбер. Нахождение точек пересечения рёбер многогранника с плоскостью, то есть нахождение вершин многогранника, получающегося в сечении.

2. Метод граней. Нахождение линий пересечения граней многогранника с секущей плоскостью, то есть нахождение сторон сечения.

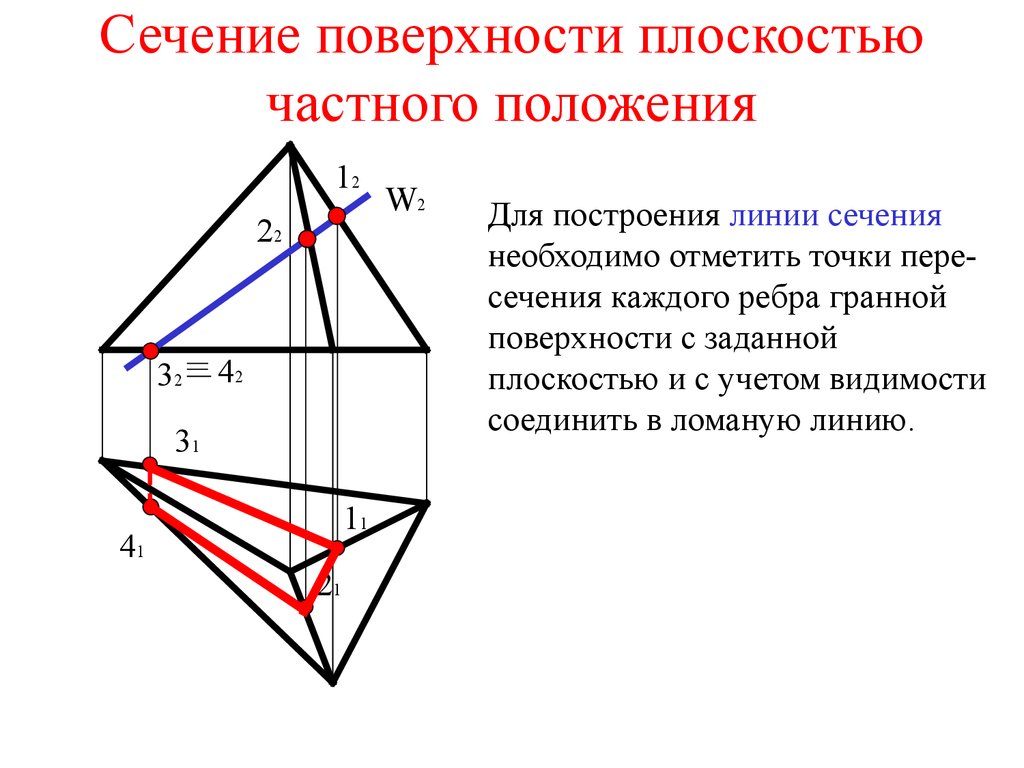
21. Пересечения многогранника плоскостью частного положения.

При пересечении многогранника плоскостью частного положения грани пересекаются по прямым линиям.

Линией пересечения будет замкнутая или незамкнутая ломаная линия.

Для построения этой линии достаточно найти точки пересечения рёбер с заданной плоскостью (опорные точки) и соединить их с учётом видимости.

22. Пересечение поверхности вращения плоскости общего положения.

При пересечении поверхности вращения с плоскостью общего положения ни одна из проекций линии пересечения не вырождается в прямую линию. Задача может быть решена с помощью общего способа: введение вспомогательных секущих плоскостей. Решение упрощается, если применить способ замены плоскостей проекций. Замену нужно произвести так, чтобы заданную плоскость общего положения в новой системе преобразовать в плоскость частного положения и решать задачу пересечения поверхности вращения с проецирующей плоскостью.

Задача: Построить линию пересечения цилиндра, поверхность Ф, с плоскостью общего положения Р заданной прямыми линиями АВ и ВС (рис.7.10).

Решение: Плоскость РАВ ВС– общего положения, а поверхность цилиндра Ф – горизонтально проецирующая, т.к. ось цилиндра перпендикулярна плоскости Н. В этом случае горизонтальная проекция искомой линии пересечения b_Н совпадает с горизонтальной проекцией цилиндра Ф_Н. Для построения фронтальной проекции линии пересечения удобно выполнить следующую замену плоскостей проекций: РАВ ВСV₁; проекции искомой линии пересечения на плоскости V₁ совпадает со следом плоскости Р – 1_V1…2_V1. Для фронтальной проекции линии пересечения необходимо построить характерные точки:

1 и 2 – высшая и низшая точки;

5 и 6 – точки видимости;

и ряд произвольных точек 3, 4, 7, 8.

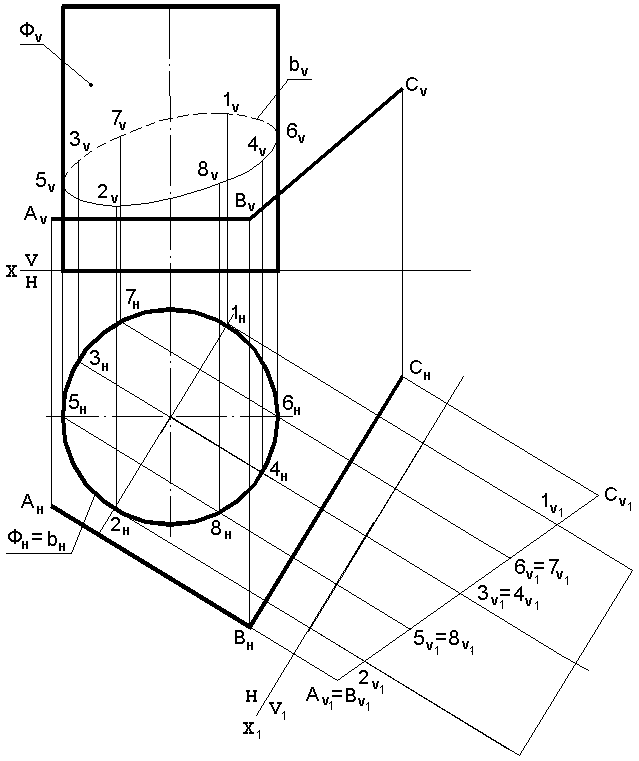
Рис.7.10. Линия пересечения цилиндра с плоскостью общего

Положения заданной прямыми линиями ав и вс

Для построения фронтальных проекций точек линии пересечения осуществляют обратную замену V₁ V, при этом сохраняется высота всех точек, т. е. =₁.

Для построения фронтальной проекции любой точки, например, точки 1, необходимо использовать условие =₁.

Полученные точки линии пересечения соединяют плавной кривой с учетом видимости. Видима та часть линии пересечения, которая расположена в передней половине поверхности цилиндра, т.е. линия 5_V,2_V,8_V,4_V,6_V, другая часть линии пересечения невидима

22. Перенесение поверхности вращение плоскостью частного положения.

В зависимости от положения секущей плоскости линия пересечения с поверхностью вращения имеет разную форму.

Цилиндр (прямой)

Если секущая плоскость параллельна основанию, то линией пересечения с прямым цилиндром является окружность. Если она расположена под углом к основанию, тогда – эллипс. В случае, когда секущая плоскость перпендикулярна основанию, линия пересечения – прямоугольник.

Сфера

Линией пересечения плоскости со сферой является окружность не зависимо от положения секущей плоскости.

Тор

Если секущая плоскость перпендикулярна оси тора, то в сечении получаем кольцо (в частном случае круг). Когда секущая плоскость расположена под иным углом к оси тора, линия пересечения представляет собой пару окружностей, эллипсов, один эллипс, либо по форме похожа на цифру «8».

Конус (прямой)

Наибольшее многообразие представляют конические сечения:

а) если секущая плоскость параллельна основанию конуса, тогда линия пересечения – окружность;

б) если секущая плоскость пересекает две образующих конуса, линия пересечения - эллипс;

в) когда секущая плоскость параллельна образующей, линия пересечения – парабола;

г) в случае, когда секущая плоскость пересекает одну образующую, линия пересечения – гипербола;

д) если секущая плоскость проходит через вершину конуса, в сечении имеем треугольник.

Рассмотрим построение проекций на примере сечения прямого конуса, основание которого параллельно плоскости П₁, различно расположенными плоскостями, которые отсекают часть конуса. Как видим, на рис. 4.8 представлено все многообразие расположения секущих плоскостей. При этом секущие плоскости являются фронтально-проецирующими, поэтому на П₂ решение получено.

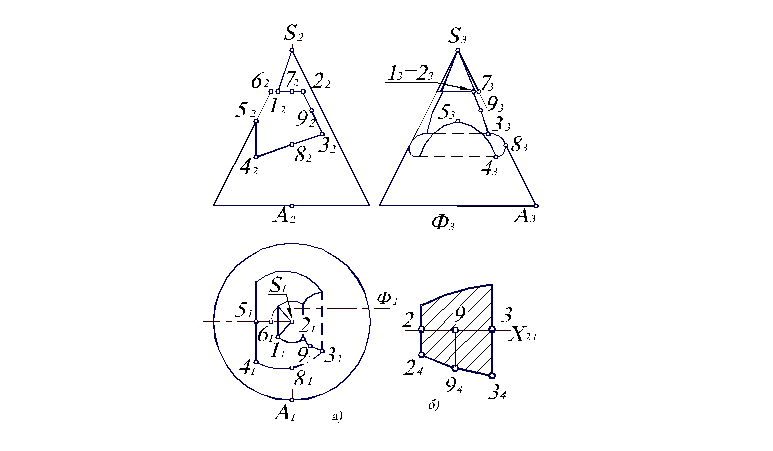
Рис. 4.8. Сечение конуса плоскостями.

Построим горизонтальную проекцию конуса, усеченного заданными плоскостями.

Линия пересечения представляет собой на участке:

S1 - отрезок прямой;

12 - дугу окружности;

23 - участок параболы;

34 – участок эллипса;

34 – гиперболу.

Для решения задачи достаточно построить горизонтальные проекции точек 1, 2, 3, 4, 5, расположенных на поверхности конуса, и соединить их линией. Например, проекция 1₁ строится так: через точку 1₂ проводим горизонтальную прямую до пересечения с контуром конуса в точке 6₂, затем радиусом S₁6₁ проводим дугу окружности и на ней по линии связи с точкой 1₂ находим точку 1₁. Аналогично строится горизонтальная проекция любой точки на поверхности конуса. Выбирая по необходимости промежуточные точки, получаем окончательное решение.

Профильную проекцию можно построить на основании правила взаимосвязи проекций. При этом необходимо учитывать контурные точки 7,8, профильные проекции которых лежат на контуре S₃A₃. Поскольку участок образующей SA между точками 7и 8 вырезан секущими плоскостями, как видно на П₂, то и на П₃ он отсутствует между точками 7₃ и 8₃.

Относительно осей Ф₁ и Ф₃ получаем симметричную картину, поэтому достаточно построить проекции на половине конуса.

На чертеже указываем линии пересечения секущих плоскостей, невидимые проекции которых обозначены пунктирной прямой.

22. Развертка многогранников.

Разверткой многогранника называется плоская фигура, составленная из его граней, совмещенных с одной плоскостью. При этом смежными будут две грани, имеющие общее ребро.

Все грани на развертке изображаются в натуральную величину, поэтому ее построение сводится к нахождению натуральных величин отдельных граней поверхности.

Для построения развертки призмы применяют два метода: нормального сечения и раскатки.

22. Развертка цилиндра поверхности.

Боковая поверхность цилиндра представляет собой прямоугольник со сторонами Н и πD. Основания цилиндра на горизонтальной плоскости проекций изображаются в натуральную величину. Для построения развертки цилиндра (рисунок 22) нужно на свободном поле чертежа провести две параллельные прямые, расстояние между ними равно высоте цилиндра – Н.

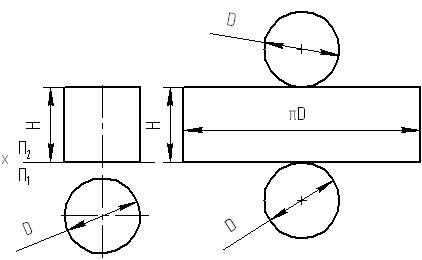
Рисунок 22

На этих прямых от произвольно выбранной точки отложить расстояние, равное длине окружности – πD. Построенный прямоугольник является разверткой боковой поверхности цилиндра. Остается пристроить окружности – основания цилиндра.

22. Построение разверток многогранников (способы)

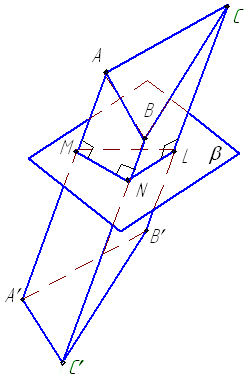
Метод нормального сечения. Нормальным сечением призмы называется ее сечение плоскостью β, перпендикулярной ребрам призмы (рис. 5.4 а). Такая плоскость пересекает призму по некоторому многоугольнику, в нашем случае треугольник MNL, стороны которого перпендикулярны ребрам призмы и равны расстояниям между соответствующими соседними ребрами призмы. Так АА'  MN, ВВ'  MN, ВВ'  NL. MN, NL и LM – соответственно расстояния между ребрами АА' и ВВ', ВВ' и СС', СС' и АА'.

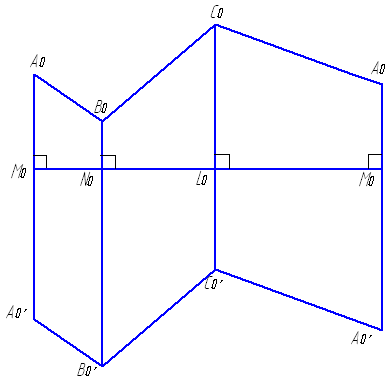
Для построения развертки такой призмы сначала следует ее нормальное сечение MNL развернуть в прямую линию М₀М₀ (рис. 5.4 б). Затем провести к этой прямой в точках М₀, N₀, L₀ перпендикуляры, на которых соответственно отложить длины ребер от нормального сечения до вершин призмы: М₀А₀ = МА, М₀А₀' = МА' и т. д. Соединив полученные точки ломаными линиями, получим развертку боковой поверхности призмы.

Ч

Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основания призмы – треугольники АВС и А'В'С', предварительно определив их натуральную величину.

а

б

Рис. 5.4 а,б

Метод раскатки. Раскатываем боковую поверхность призмы на плоскости чертежа одну грань за другой.

Этот способ наиболее эффективен тогда, когда основание призмы проецируется в натуральную величину на плоскость проекций.

Пример 5.4. Построить развертку прямой пятиугольной призмы частного положения (рис. 5.5).

Рис.5.5

1. Ребра основания проецируются в натуральную величину на П₁, а длину боковых ребер измеряем на П₂.

2. Отметим в произвольном месте чертежа точку А₀ на горизонтальной линии. Строим последовательно В₀, С₀, D₀, E₀, A₀, перенося на эту линии длину отрезков A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁A₁. В результате раскатываем все боковые грани призмы.

3. Строим на одной из сторон, например D₀E₀, нижнее основание, применяя метод триангуляции. Аналогично строим верхнее основание.

22. Построение развёртки тел вращения

75