6. Перспектива интерьера (особенности выбора точек и углов зрения).

Опыт построения интерьеров показывает, что наилучшее перспективное изображение интерьера получается, если угол построения выбирать в пределах 37°–53°.

Фронтальная перспектива отличается простотой построения и широко используется при построении интерьеров.

При построении композиции интерьера главную точку картины Р можно расположить на линии горизонта различно. Если точка Р располагается в самом центре картины, то изображение называется центральной фронтальной перспективой. Если точка Р смещается вправо или влево по линии горизонта, то изображение называется боковой фронтальной перспективой. При точке Р, сдвинутой влево, правая стена комнаты будет больше, чем левая, и наоборот, если точка Р сдвигается вправо, то левая стена будет больше правой.

Следовательно, в зависимости от характера композиции картины художник перемещает главную точку Р по своему усмотрению.

Высота линии горизонта выбирается в соответствии с высотой глаз человека среднего роста и обычно берется 1,5, 1,6 или 1,75 м.

Дистанционная точка D в небольших помещениях выбирается на расстоянии, равном диагонали картины.

При построении угловой перспективы интерьера важным вопросом является компоновка чертежа и определение на картине основных ее элементов: линии горизонта hh, главной точки Р, точек отдаления F, F1 и угла зрения. Как уже говорилось, картина должна быть расположена в наилучшем поле зрения, т. е. с углом зрения, равным примерно 28–53°.

Блок 2

1. Сущность метода проекций.

Метод проекций обеспечивает построение изображений пространственных форм на плоском чертеже.

Аппарат проецирования включает:

- проецирующие лучи,

- проецируемый объект

- плоскость, на которой получается изображение объекта.

Любой материальный объект можно представить состоящим из множества точек, которые могут быть спроецированы на плоскость. В этом случае проекции точек формируют плоское изображение объекта.

Свойства полученных проекций во многом определяются положением центра проекций S по отношению к плоскости П´.

При этом различают центральное и параллельное проецирование.

2. Центральное и параллельное проецирования.

Если все проецирующие лучи исходят из собственной точки (точки, находящейся в обозримом пространстве), то проецирование называется центральным, а саму точку - источник проецирующих лучей, называют центром проецирования. Обычно центр проекций обозначают буквой S.

Таким образом, аппарат проецирования включает в себя: центр проецирования, проецирующие лучи и плоскость проецирования. Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пересечения этой прямой с плоскостью проекций и является центральной проекцией заданной точки на выбранной плоскости проекций.

Свойства центрального проецирования

1. Проекция точки есть точка.

2. Проекция линии есть линия.

3. Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии.

4. Точка пересечения линий проецируется в точку пересечения проекций этих линий.

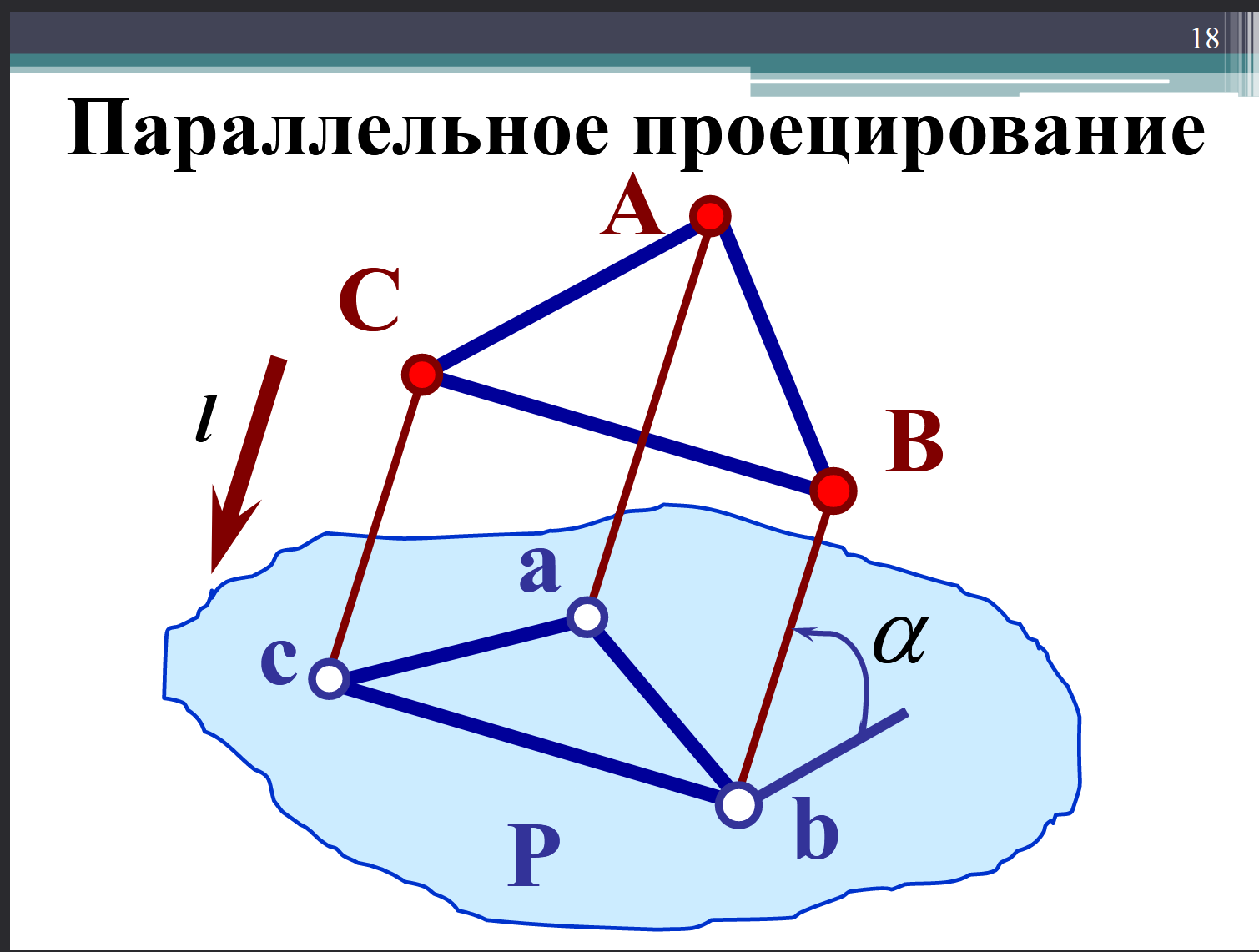
Параллельное проецирование.

Параллельное проецирование можно рассматривать как частный случай центрального проецирования, при котором центр проекций удален в бесконечность (S ).

При параллельном проецировании применяют параллельные проецирующие прямые, проведенные в заданном направлении отностиельно плоскости проекций. Если направление проецирования перпендикулярно плоскости проекций, то проекции называют прямоугольными или ортогональными, в остальных случаях - косоугольными.

При параллельном проецировании сохраняются все свойства центрального проецирования, а также возникают новые свойства.

Параллельные проекции, как и центральные при одном центре проекций, также не обеспечивают обратимости чертежа. Применяя приемы параллельного проецирования точки и линии, можно строить параллельные проекции поверхности и тела.

3. Основные свойства параллельных проецирования.

1. Свойство однозначности. Проекцией точки на плоскость есть точка.

2. Свойство прямолинейности. Проекцией прямой линии на плоскость есть прямая.

3. Свойство принадлежности. Если точка принадлежит линии, то проекция точки принадлежит проекции этой линии.

4. Свойство сохранения параллельности. Проекциями параллельных прямых являются параллельные прямые.

5. Свойство деления отрезка в отношении. Если отрезок прямой линии делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении.

6. Свойство параллельного переноса. Проекция фигуры не меняется при параллельном переносе плоскости проекций.

Три последние свойства обеспечивают более простое построение изображения и меньше искажают форму и размеры оригинала по сравнению с центральной проекцией.

4. Ортогональная система двух и трех плоскостей проекции.

ОРТОГОНАЛЬНАЯ ДВУХМЕРНАЯ СИСТЕМА ПРОЕКЦИЙ

Ортогональное проецирование состоит в смещении предмета на две взаимно перпендикулярные плоскости с помощью лучей, перпендикулярных к этим плоскостям.

Плоскости проекции располагаются горизонтально и вертикально.

Плоскость H называется горизонтальной плоскостью проекций, а плоскость V — фронтальной. Плоскости H и V бесконечны и непрозрачны. Плоскостями проекций пространство делится на четыре двугранных угла — четверти. Линия пересечения плоскостей проекций называется осью координат и обозначается OX.

Будем считать, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций. В связи с тем, что плоскости проекций непрозрачны, видимыми для наблюдателя будут только точки, линии и фигуры, расположенные в пределах той же первой четверти.

Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость.

Эпюр - это проекционный чертеж, на котором плоскости проекций со всем изображенным на них совмещены определенным образом

ОРТОГОНАЛЬНАЯ СИСТЕМА ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИИ

5. Эпюр точки и прямой.

ЭПЮР ТОЧКИ

6. Различные положения прямой линии отосит. п.п.

• Прямая, не параллельна ни одной из плоскостей проекций, H прямой общего положения

• Прямые параллельны или перпендикулярный плоскостям проекций, H прямой частного положения

• Прямые параллельны плоскости проекции, линия уровня (прямая, параллельная H горизонтальная)

• Прямые, перпендикулярны п.п. – проецирующие (прямая, перпендикулярная H – горизонтально и проецирующ.)

7. Следы прямой линии.

Точка пересечения прямой с плоскостями проекций. Для определения на эпюре горизонтального следа прямой необходимо проложить ее фронтальную проекцию до пересечения с осью Ох и в этой точке восстановить перпендикуляр до пересечения с горизонтальной проекцией прямой.

8. Определения натуральной величины отрезка прямой линии.

Ортогональная проекция отрезка прямой общего положения всегда меньше длины самого отрезка.

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

9. Взаимное расположение двух прямых линий.

• Пересекающиеся прямые

• Параллельные прямые

• Скрещивающиеся прямые (если не параллельны и не прямые, т.е. не лежат в одной плоскости)

10. Способы задания и изображения плоскости

1) тремя точками, не лежащими на одной прямой

2) прямой и точкой, не лежащей на этой прямой

3) двумя параллельными прямыми

4) двумя пересекающимися прямыми

5) плоской фигурой

6) масштабом уклонов

11. Плоскости общего положения. Следы плоскости.

П лоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Эта плоскость произвольно наклонена к осям проекций и на эпюре ее следы составляют с координатными осями произвольные углы наклона

Положение плоскости в пространстве может быть определено ее следами.

След плоскости - прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций

В общем случае плоскость имеет три следа – горизонтальный, фронтальный и профильный, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃

В точках а_x, а_y, а_z, лежащих на осях координат, следы плоскости пересекаются. Эти точки называются точками схода следов плоскости.

Если прямая АВ лежит в плоскости Р, то она пересечет плоскость П₁ в точке М₁ расположенной на линии Р₁, т.е. горизонтальный след прямой, лежащей в плоскости, расположен на горизонтальном следе плоскости.

Иными словами, следы прямой, лежащей в плоскости, расположены на одноименных следах плоскости. Отсюда следует, что следы плоскости должны проходить через одноименные следы прямых, лежащих в плоскости.

Чтобы построить след плоскости, необходимо определить следы двух прямых, лежащих в плоскости.

На рисунке плоскость задана двумя пересекающимися прямыми АВ и СD. Чтобы построить горизонтальный след плоскости необходимо найти горизонтальный след прямой АВ – точку М и прямой СD – точку М¹. Горизонтальный след плоскости будет проходить через точки М и М¹. Фронтальный след плоскости Р₂ строится аналогично. Следует отметить, что для построения следа Р₂ достаточно иметь фронтальный след только одной прямой, так как второй точкой, определяющей положение следа Р₂ будет точка Р_х схода следов (точка пересечения ранее построенного следа Р₁ с осью х).