Аксонометрические проекции. Связь между коэффициентами искажения и направлением проецирования. Стандартные аксонометрические проекции (ортогональные и косоугольные).
Аксонометрическая проекция — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций. При этом предмет проецируется на произвольную плоскость, которая не совпадает с его координатной плоскостью. В результате получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение предмета в пространстве и получить наглядное изображение.
Связь между коэффициентами искажения и направлением проецирования определяет тип аксонометрической проекции. Если все три коэффициента искажения равны между собой, проекция называется изометрической, если равны только два коэффициента — диметрической, а если коэффициенты неравны — триметрической. Если направление проецирования перпендикулярно плоскости проекций, проекция называется прямоугольной, а если направление проецирования не перпендикулярно плоскости проекций — косоугольной
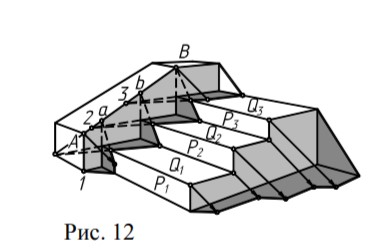
Тень лестницы:
Построена продолжением плоскостей ступеней до пересечения с прямыми, дающими тень на эти плоскости, т.е. использован след прямой на плоскости тени
Тень цилиндрической колонны с квадратной плитой: этот пример полная аналогия построения теней в аксонометрии в перспективе. Отличие в наличии на перспективном изображении двух точек схода перспектив параллельных ребер на линии горизонта и точек схода перспектив лучей S и их вторичных проекций s
Перспектива
Перспектива - различные способы и приёмы изображения объёмных объектов и пространственных отношений на плоскости.
• Виды: прямая линейная, параллельная (латеральная), обратная, усиленно сходящаяся, соединенная прямой/аксонометрической и прямой, сферическая, воздушная, панорамная, тональная
• Линейная перспектива: фронтальная, угловая, мультиточечная и перспектива в три точки схода
Перспектива окружности
• Способ 1. Для получения перспективы окружности (или любой другой кривой линии) строится перспектива достаточно большого числа её точек, которые соединяются плавной кривой линией. Перспектива каждой точки строится при помощи двух вспомогательных прямых или другим способом.
• Способ 2. Около заданной окружности (или другой кривой линии) описывается квадрат (или другой многоугольник), строится перспектива квадрата или многоугольника и в него вписывается в перспективе кривая - перспектива заданной кривой.
• Перспектива параллельных окружностей
Линейная перспектива
Линейная перспектива - способ изображения пространства так, как его видит человеческий глаз
Точка зрения должна выбираться на таком расстоянии от объекта, чтобы его можно было легко охватить одним взглядом. Горизонтальные углы зрения между крайними лучами в плане должны находиться в пределах от 20 до 50°
Горизонтальный угол 50° — это предельная величина угла зрения. Лучшими углами следует считать углы 30 — 40°. С более близких точек зрения рассматривать объекты целиком трудно, а на перспективных изображениях, построенных с этих точек зрения, возникают чрезмерные перспективные искажения.
Виды перспективы в зависимости от положения картинной плоскости и высоты точки зрения.
Виды:
Прямая – с единой точкой схода на горизонте;
Обратная – с центром схода линий на наблюдателе;
Панорамная – основанная на цилиндрической или сферической поверхности;
Тональная – созданная на цвете и контрасте объекта;
Воздушная – со снижением четкости границ при отдалении от точки зрения.
Построение перспективы способом архитекторов (с двумя и одной точками схода).
Исходными данными для построения перспективы является ортогональные проекции данного объекта и положение линии горизонта.
• Построение с одной точкой схода (объяснение и пример)
При построении перспективы в первую очередь строиться вначале перспектива плана. Главная ось картины РР1 выбирается так, чтобы обе точки схода, по возможности, поместились в пределах чертежа. С ортогонального чертежа на основание картины в перспективе переносятся картинные следы прямых плана (точки 11,21,31), а на линию горизонта – точки схода (F1+ и F1-). Расстояния между точками в перспективе должны соответствовать их расстоянию в ортогональных проекциях или увеличены, если принимается масштаб увеличения. Соединив картинные следы (т. 1,2,3) с соответствующими точками схода (F1+ и F1 -), получим перспективу прямых плана и контур перспективы плана.
Для построения перспективы вертикальных ребер проводятся вертикальные прямые. Ребро, проходящее через точку 21, лежит в картинной плоскости, следовательно, в перспективе оно изобразится в натуральную величину (с учетом масштаба при выполнении перспективы). Через верхнюю точку ребра проводятся прямые в точки схода F1+ и F1 -.
Высота остальных вертикальных прямых определяется до точки пересечения лучей, идущих в точки схода. Эти прямые будут определять положение крайних вертикальных ребер здания в перспективе. Вершины этих ребер соединяются с точками схода, и в пересечении этих лучей определяется положение вершины дальнего ребра здания.
