6. Способ лучевых поверхностей

Это основной и универсальный способ построения теней. Применяется при построении падающих, а также собственных теней сложных по форме объектов. Не сложен, но требует много графических операций.

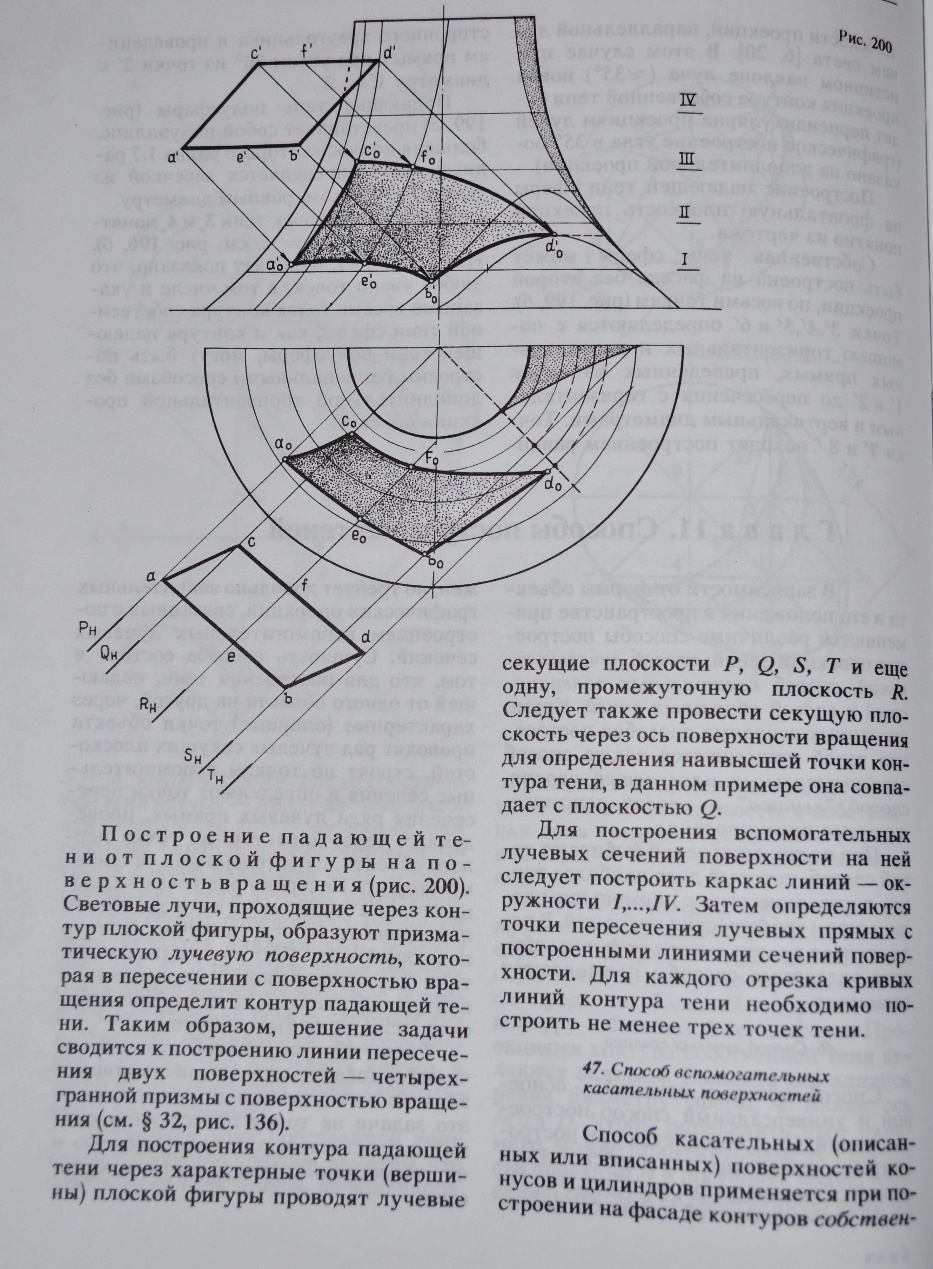
Сущность – для построения падающей тени через характерные (опорные) точки объекта проводят ряд лучевых секущих плоскостей, по которым строят вспомогательные сечения. Затем определяют точки пересечения потока лучевых прямых со вспомогательными сечениями. Соединив их определенным образом, получают контур падающей тени.

Построение падающей тени от плоской фигуры на поверхность вращения. Световые лучи, проходящие через контур плоской фигуры, образуют призматическую лучевую поверхность, которая при пересечении с поверхностью вращения даст контур падающей тени.

6. Способ касательных поверхностей при построении теней.

Способ вспомогательных касательных (описанных или вписанных) поверхностей конусов или цилиндров применяется при построении на фасаде контуров собственных теней поверхностей вращения без второй проекции.

Сущность (рис. 201). Для построения точек, принадлежащих контуру собственной тени, используются вспомогательные цилиндрические или конические поверхности, тени которых определяются просто. Эти поверхности касаются заданной поверхности вращения по окружностям – параллелям.

Нужно вычленить из сложной фигуры цилиндры и конусы. Затем построить их тени. Найти характерные точки (те что лежат на фигуре) и соединить их. Построить контур тени по этим точкам

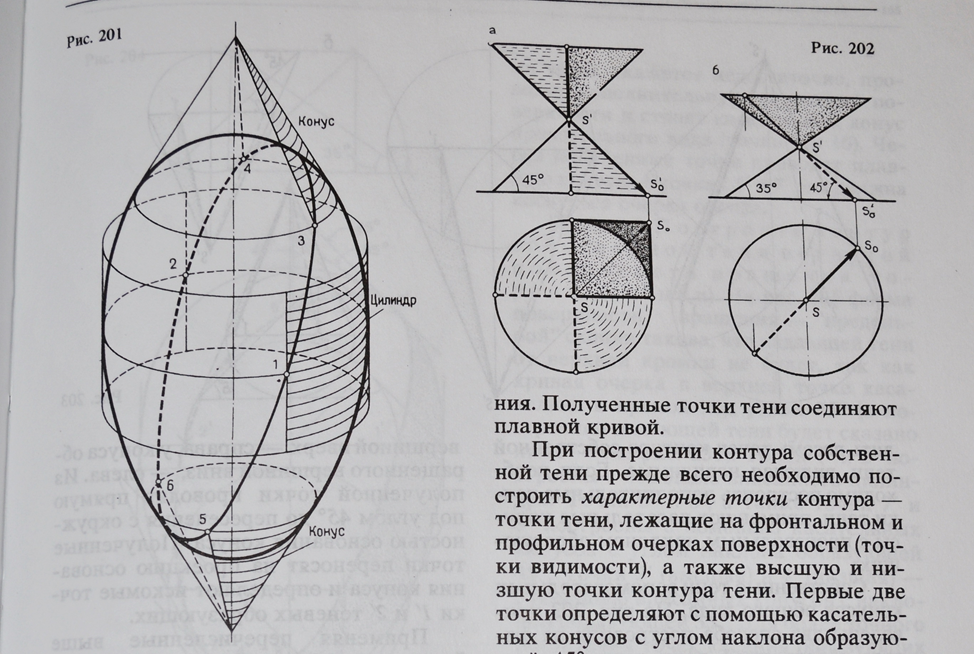
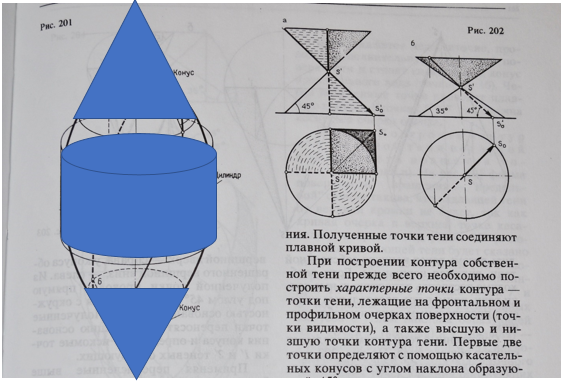
Собственная тень сферы и валика в ортогональных проекциях.

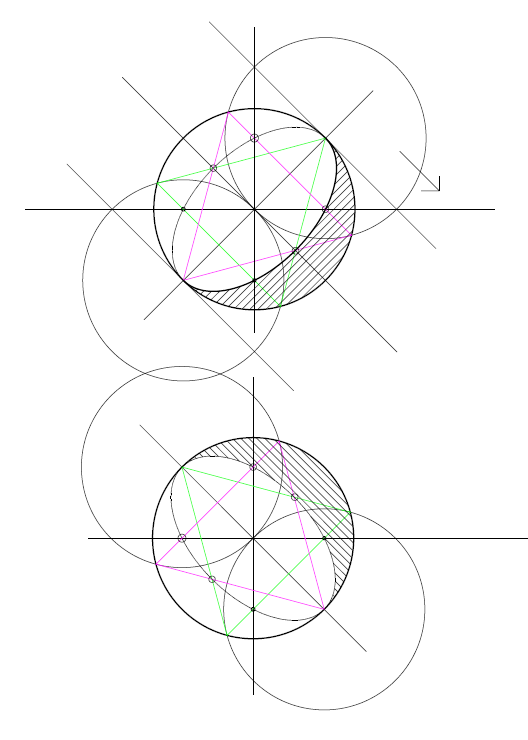
Строим центральную ось под 90 к углу падения солнечных лучей, находим характерные точки с помощью доп построения 2х окружностей и строим тень.

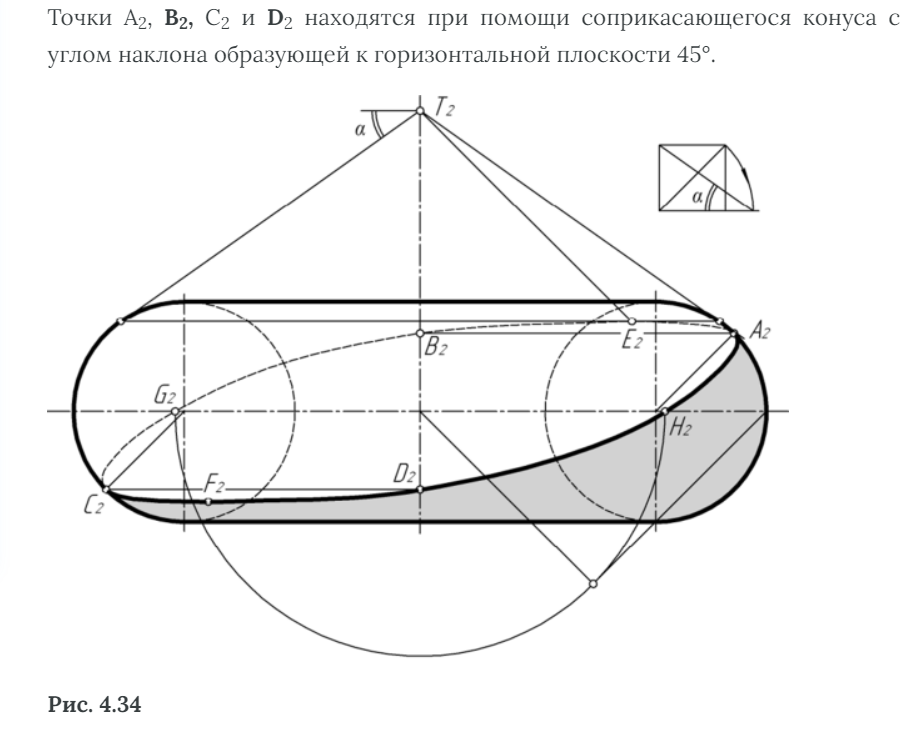
Точки Е₂ и F₂ (самая высокая и самая низкая) строятся при помощи соприкасающегося конуса с углом наклона образующей к горизонтальной плоскости а=35°15'52". Построение угла а показано справа вверху на рис.4.34. (построение конусов можно посмотреть в предыдущем пункте)

Точки G₂ и Н₂ строятся при помощи соприкасающегося цилиндра вращения.

Затем все точки соединяются лекальной линией, как показано на рис.4.34. Необходимо учитывать, что в точках Е₂ и F₂ граница собственной тени касается параллелей тора (на фронтальной проекции - горизонтальных прямых), а в точках А₂, и С₂ она касается очерка тора.

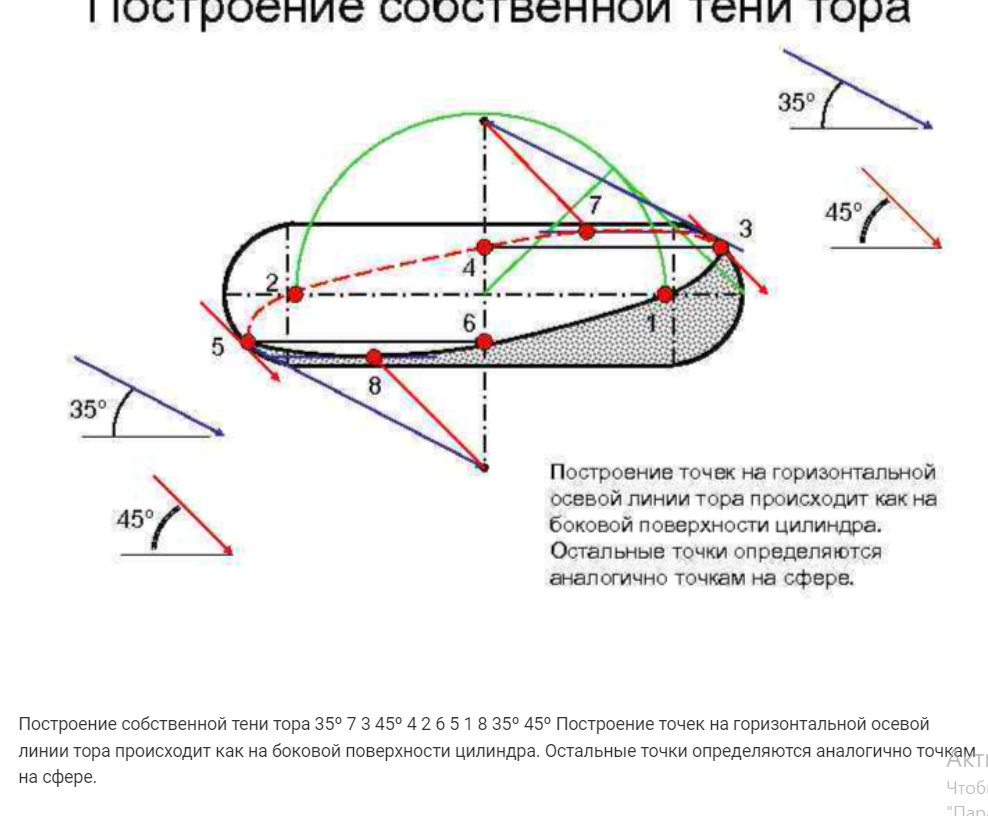
6. Способ выноса при построении теней. Падающая тень от сферы в ортогональных проекциях.

Способ "выноса" (ординат) при­меняется для построения падающих теней на плоскостях проекций и пло­скостях уровня.

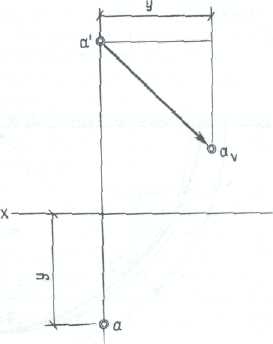
Если известно рассто­яние (вынос) отдельных точек объекта, например от фронтальной плоскости, падающая тень может быть построена без горизонтальной проекции, по выно­су (ординатам у) этих точек.

Для построения тени точки А на фронтальной плоскости проекций (рис. 208) следует от проекции точки а' отло­жить вправо величину выноса у и по­строить в пересечении с проекцией лу­ча тень av точки.

6. Тени карнизов в ортогональных проекциях.

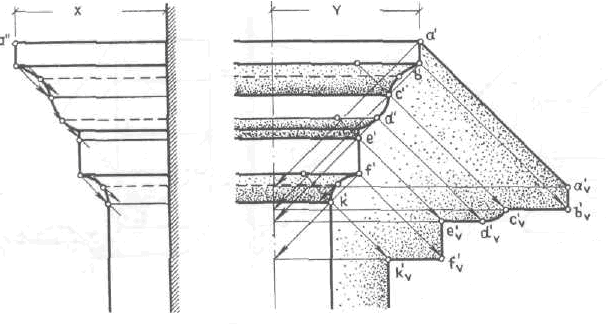
Это тоже способ выноса, без горизонтальной проекции. Лучи падают по 45 от оси, падающую тень образуют точно которые не находятся в собственной тени.

6. Тени кронштейнов в ортогональных проекциях

Тени кронштейнов. Форма кронштейна представляет собой цилиндрическую поверхность различного профиля, ограниченную параллельными плоскостями. Построение собственных и падающих теней кронштейна, имеющего выпуклые и вогнутые части цилиндрической поверхности, выполняют с помощью профильной проекции. Профильные проекции лучей, касательные к профилю кронштейна, определяют контуры собственной тени. Для более точного построения кривой контура падающей тени на стену следует изобразить и мнимые участки тени.

6. Тени в ортогональных проекциях комбинированной (сферической – цилиндрической) ниши.

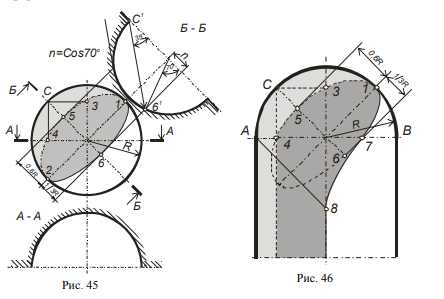
Ниши обычно имеют форму поверхностей второго порядка, поэтому падающая тень от кромки ниши на ее внутреннюю поверхность будет плоской кривой того же порядка (на основе теоремы Монжа о плоских сечениях). Это позволяет упростить построение, выполняя его по одной проекции, используя опорные точки.Наклонное сечение Б-Б позволяет увидеть построение точки 6 на малой оси эллипса падающей тени. Контур собственной тени (1, 2, 3, 4, 5) построен с использованием касательных конусов. Расстояние от центра сферы до точки 5 (малая полуось эллипса) равно 0,57R ≈ 0,6R. Расстояние от центра сферы до точки 6 равно примерно 1/3R, (точнее cos 70o = 0,342).

Полуэллипс (1 6 2) – контур падающей тени – можно построить по трем точкам. Кстати, любая точка этой кривой отстоит от линии (1 2) на 1/3 своей полухорды в направлении, параллельном малой оси эллипса. На рис. 46 построены собственная и падающая тени полуцилиндрической ниши со сферическим завершением. АВ – граница перехода, на которой лежат пограничные точки 4 и 7. В точке 4 виден излом при переходе собственной тени сферы в тень цилиндра. Точка 8 – тень от точки А. Контур падающей тени не должен иметь излома, так как поверхности цилиндра и сферы касательные.

6. Тени в ортогональных проекциях схематизированной капители

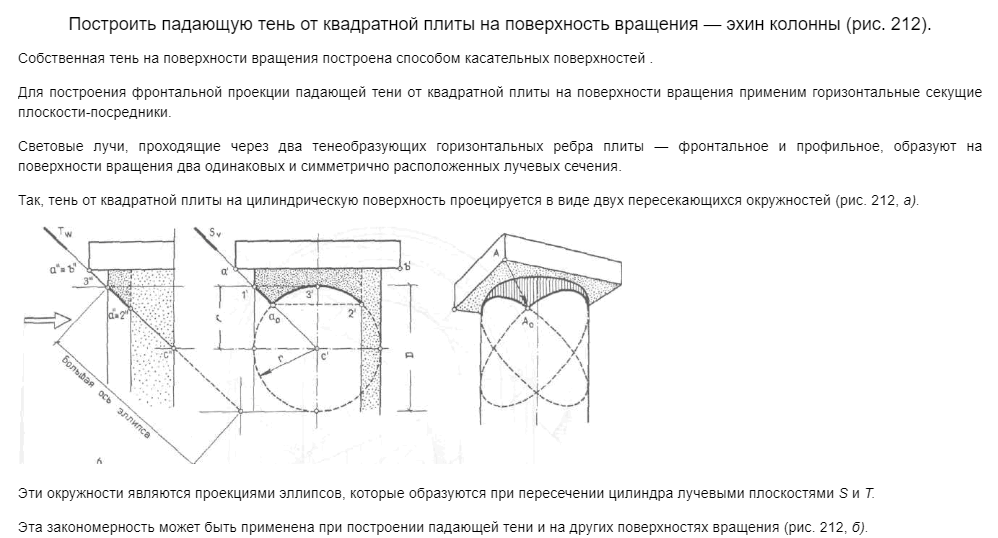
Все элементы теней этого архитектурного фрагмента были рас­смотрены ранее (см. рис. 210, 212).

Соб­ственная тень полувалика (эхина) по­строена способом касательных поверх­ностей. Падающая тень от эхина на колонну построена с помощью тени на вспомога­тельной меридиональной плоскости (см. рис. 233).

Точка тени а₀ является точкой пересечения контуров падаю­щих теней от двух горизонтальных ре­бер квадратной плиты на ствол колон­ны.

Следует обратить внимание на чет­кую взаимосвязь контуров теней, а так­же на следующие закономерности:

1. точка исчезновения тени и точ­ка пересечения контуров падающих теней лежат на одном луче, это точки 2' и 2’o, 3' и 3v, 4’₀ и 4v

2. в точках 2', 3' и 4'₀ исчезновения тени, где контур падающей тени пересекает контур собственной тени, ли­ния контура падающей тени касательна к проекции луча.

Падающие тени от квадратной плиты (абаки) на эхин и на колонну построены способом горизонтальных плоскостей уровня и с помощью лучевого сечения колонны фронтально про­ецирующей плоскостью (см. рис. 212).

6. Тени в ортогональных проекциях комбинированной (тороидальной - цилиндрической) ниши.

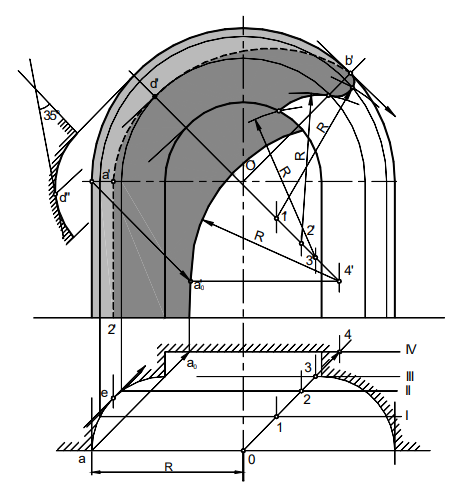
Поверхность ниши образована тороидальной и цилиндрической поверхносятми и фронтальной плоскостью. Собственная тень ниши построена с помощью вспомогательного сечения, проведенного в плоскости луча (точка d’). Для построения падающей тени от кромки ниши проведены четыре фронтальные плоскости посредники и построены сечения ниши этими плоскостями. Затем на каждой плоскости сроят тени от кромки ниши – засечки другой окружности радиуса R. Центры 1,2,3,4 вспомогательных окружностей смещаются от проекции луча. В точке b’ контур падающей тени должен коснуться кромки ниши.

6. Аксонометрические проекции. Виды аксонометрических проекций.

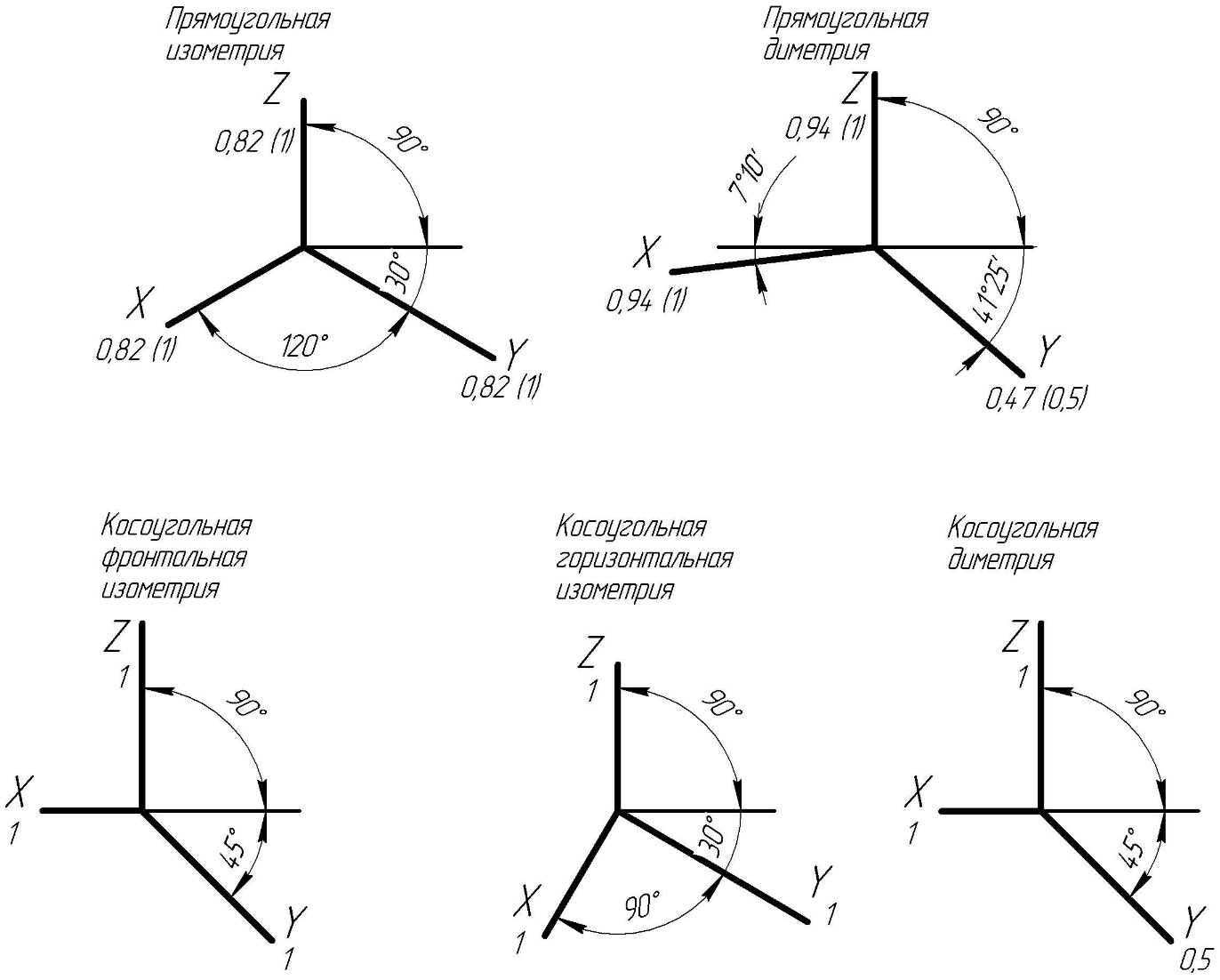
Аксонометрическая проекция — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций. При этом предмет проецируется на произвольную плоскость, которая не совпадает с его координатной плоскостью. В результате получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение предмета в пространстве и получить наглядное изображение.

Виды аксонометрических проекций включают прямоугольные и косоугольные проекции. Прямоугольные проекции делятся на изометрические и диметрические, а косоугольные проекции включают фронтальные диметрические, фронтальные изометрические и горизонтальные изометрические проекции.