3. Тени призмы и пирамиды в ортогональных проекциях.

ТЕНЬ ПРИЗМЫ

На рисунке 89, 90 построены собственная и падающая тени прямой пятиугольной призмы.

Рис. 89

Рис. 90

Для определения контура собственной тени призмы необходимо установить освещенность ее граней. Так как боковые грани призмы перпендикулярны к плоскости Н, то их освещенность легко определить на горизонтальной проекции, где видно, что обращены к свету две грани: EFGK и KGAB.

ТЕНЬ ПИРАМИДЫ

На рисунке 91,92 приведен пример построения собственной и падающей теней правильной пятиугольной пирамиды SABCDE.

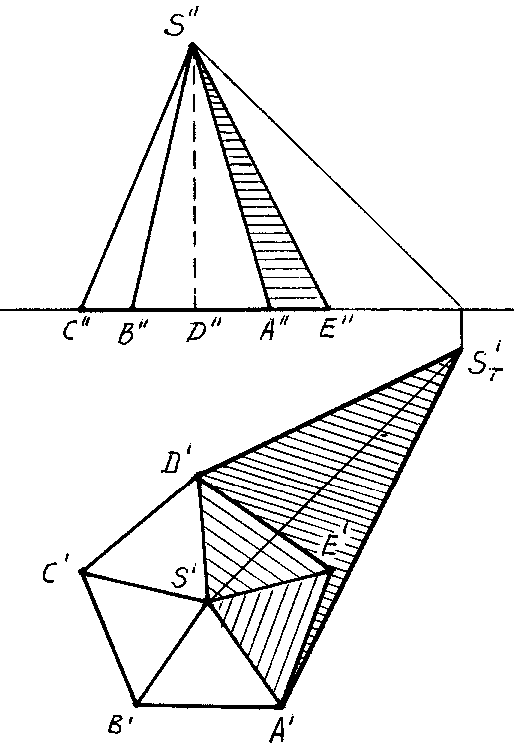
Рис. 91 Рис. 92

В отличие от прямой призмы, боковые грани пирамиды не являются горизонтально-проецирующими плоскостями, поэтому определить их освещенность непосредственно по горизонтальной проекции не всегда возможно.

Строим падающую тень ST' от вершины S на плоскость Н и определяем падающие тени от боковых ребер пирамиды. Линиями контура падающей тени пирамиды оказались прямые ST'А и ST'D. Следовательно, контур собственной тени пройдет вдоль ребер SA и SD. Таким образом, в собственной тени будут находиться грани SAE,SDE и основание пирамиды.

4. Тень цилиндра и конуса в ортогональных проекциях.

ТЕНЬ ЦИЛИНДРА

Две плоскости Р и Q – касательные к цилиндру (рис. 12 а) дают собственные и падающие тени. Тень от верхнего основания строится по точкам 1, 2, 3, 4, 5.

Падающая тень от цилиндра на стену по ширине равна 1,4 диаметра цилиндра. В точках 1v и 5v – прямые, касательные к кривой. Тень от полуцилиндра на стенку строится по размеру х (рис 12 б).

ТЕНЬ КОНУСА.

Поверхность конуса – это единственная поверхность, для построения

контура собственной тени которой надо сначала построить падающую тень на плоскость его основания.

1. Через вершину S (рис. 14 а и 14 б) проводится луч SSh (обратный SS0 – для обратного конуса).

2. Находится точка его пересечения с плоскостью основания конуса Sh (S0).

3. Из полученной точки Sh (или S0) проводятся касательные Sh1, Sh2 (S01, S02) к основанию конуса. Эти точки касания 1 и 2 определяют образующие конуса S1, S2 – границу собственной тени.

У прямого конуса в тени будет меньше половины поверхности, у обратного – больше половины.

5. Способ обратного луча при построении теней.

СПОСОБ ОБРАТНЫХ ЛУЧЕЙ

Способ обратных лучей применяется для построения падающих теней от одного предмета на другой. Способ основан на том, что точки пересечения теней, падающих от двух линий на плоскость, являются совпавшими тенями точек этих линий, лежащих на одном световом луче.

Рассмотрим построение тени от двух прямых SF и SB на непрозрачную пластинку ECDF. (рисунок 5.2).

Тень от проецирующей прямой SA строится методом лучевых сечений. На горизонтальной проекции тень совпадает с направлением луча, на фронтальной - идет по лучевому сечению. Тень от точки S на пластину ESDF не надает. Для построения тени от наклонной прямой SB на пластину ESDF, необходимо построить сначала тень падающую на плоскость   Для чего строим тень от точки S падающую на  и полученную точку  соединяем с точкой   т.к. точка В лежит на плоскости 

Далее строим тень от пластины ESDF на плоскость  для чего строим тени точек С и D и соединяем их с точками  лежащими на плоскости Полученные тени пересекаются    в точке   . Из точки пересечения теней проводим обратный луч под углом 45° на прямую   По вертикальной линии связи находим фронтальную проекцию этой точки. Обратите внимание, что точки 1 и 3, являются точками излома теней падающих на горизонтальную плоскость и на наклонную плоскость а.

Необходимо отметить что данную задачу можно решить используя построение мнимой тени от точки S на пластину ESDF (рисунок 5.3).