Экзамен начертательная геометрия 06.07.2024 г.

	Оглавление	Стр
	Блок 1	3
1	Тень точки и отрезка прямой в ортогональных проекциях	3
2	Тени плоских фигур в ортогональных проекциях	7
3	Тени призмы и пирамиды в ортогональных проекциях	8
4	Тень цилиндра и конуса в ортогональных проекциях	10
5	Способ обратного луча при построении теней	12
6	Способ лучевых сечений при построении теней. Тень от пластины на кривую поверхность в ортогональных проекциях	14
7	Способ касательных поверхностей при построении теней. Собственная тень сферы и валика в ортогональных проекциях	15
8	Способ выноса при построении теней. Падающая тень от сферы в ортогональных проекциях	18
9	Тени карнизов в ортогональных проекциях	20
10	Тени кронштейнов в ортогональных проекциях	20
11	Тени в ортогональных проекциях комбинированной (сферической – цилиндрической) ниши	22
12	Тени в ортогональных проекциях схематизированной капители	23
13	Тени в ортогональных проекциях комбинированной (тороидальной - цилиндрической) ниши	25
14	Аксонометрические проекции. Виды аксонометрических проекций	26
15	Аксонометрические проекции. Связь между коэффициентами искажения и направлением проецирования. Стандартные аксонометрические проекции (ортогональные и косоугольные)	27
16	Тени в аксонометрии: лестницы, цилиндрической колонны с квадр. плитой	28
17	Перспектива: определение, виды, компоненты линейной перспективы	29
18	Перспектива окружности. Перспектива параллельных окружностей	29
19	Выбор картины, точки зрения и углов при построении линейной перспективы	31
20	Виды перспективы в зависимости от положения картинной плоскости и высоты точки зрения	32
21	Построение перспективы способом архитекторов (с двумя и одной точками схода)	32
22	Метод сетки в построении перспективы (привести пример с построением теней)	33
23	Построение теней в перспективе	35
24	Перспектива интерьера (особенности выбора точек и углов зрения). Привести пример	37
	Блок 2	40
1	Сущность метода проекций	40
2	Центральное и параллельное проецирования	40
3	Основные свойства параллельных проецирования	42
4	Ортогональная система двух и трех плоскостей проекции	42
5	Эпюр точки и прямой	45
6	Различные положения прямой линии отосит. п.п	45
7	Следы прямой линии	46
8	Определения натуральной величины отрезка прямой линии	46
9	Взаимное расположение двух прямых линий	47
10	Способы задания и изображения плоскости	48
11	Плоскости общего положения. Следы плоскости	49
12	Плоскости частного положения. Их свойства	50
13	Главные линии плоскости	52
14	Различное положения прямой линии и плоскости	53
15	Различное положения двух плоскостей	54
16	Перпендикулярность прямой и плоскости	55
17	Определение линии пересечения двух плоскостей	56
18	Способы преобразования прямой	56
19	Способы замены плоскостей проекций	57
20	Пересечения многогранника плоскостью общего положения	58
21	Пересечение многогранника плоскостью частного положения	59
22	Пересечение поверхности вращения плоскости общего положения	59
23	Перенесение поверхности вращение плоскостью частного положения	61
24	Развертка многогранников	64
25	Развертка цилиндра поверхности	64
26	Построение разверток многогранников (способы	65
27	Построение развёртки тел вращения	67
	Задачи
1	Построить пересечение геометрических фигур
2	Построить сечение фигур плоскостью
3	Построить пересечение плоскостей
4	Построить пересечение плоскости и отрезка
5	Построить тени в ортогональных проекциях
6	Построить тени в перспективе
7	Построить тени в аксонометрии
8	Построить перспективу
9	Построить аксонометрию

Блок 1

1. Тень точки и отрезка прямой в ортогональных проекциях.

Падающая тень от точки

Представим себе материальную точку А(рис. 74), расположенную в пространстве над плоскостью Н, которая освещается световыми лучами, идущими из бесконечности параллельно заданному направлению. Точка А задержит один из них и отбросит теневой луч, который пересечет плоскость Н в точке АТ'. Эта точка и будет являться тенью точки А.

Иными словами, тень точки является следом теневого луча.

Итак, чтобы построить тень, падающую от точки на какую-либо плоскость или поверхность, необходимо через данную точку провести прямую, параллельную направлению лучей света, и определить точку пересечения этой прямой с плоскостью или поверхностью, на которую падает тень.

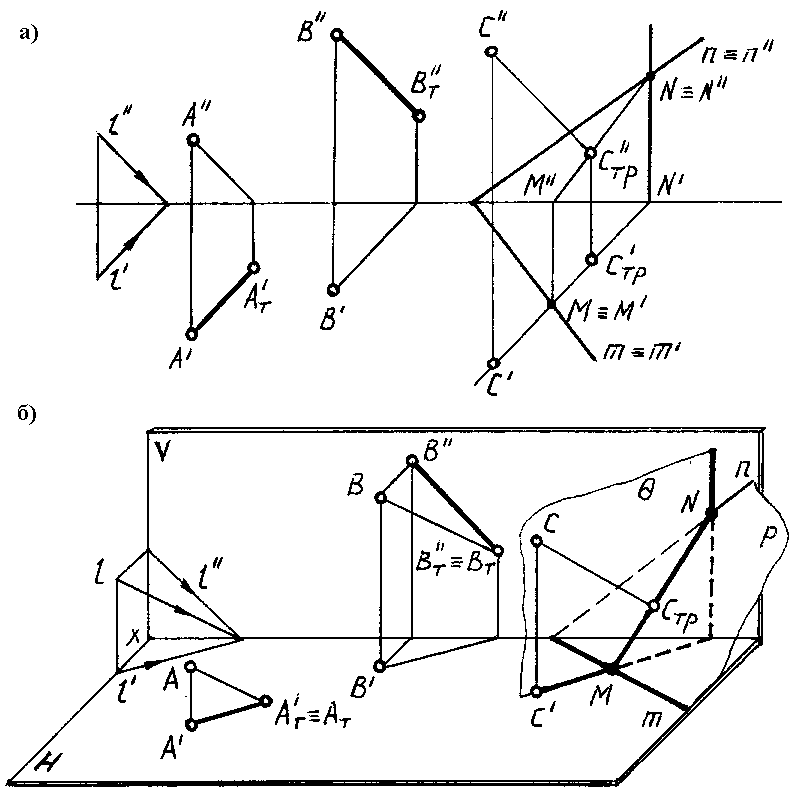
На рис. 75а в ортогональных проекциях и на рис. 75б в аксонометрии построены тени, падающие на плоскости Н, V и P(nm) от точек А,В и С.

Тень от точки А падает на плоскость Н в точке АТ' (эта точка является горизонтальным следом луча ААТ).

Тень от точки В падает на плоскость V в точке BТ'' (эта точка является фронтальным следом луча АВТ).

Тень от точки в аксонометрии определяется в результате пересечения луча с его вторичной проекцией.

Тень ВT'' (в аксонометрии) можно построить как точку пересечения луча ВВТ с его фронтальной проекцией В''BT''или при помощи горизонтальной проекции луча.

Тень от точки Спадает на плоскость P (nm) в точке СTP (СTP', СTP”), которая определяется в результате пересечения луча ССT с заданной плоскостью Р при помощи горизонтально-проецирующей плоскости

Падающая тень от прямой линии

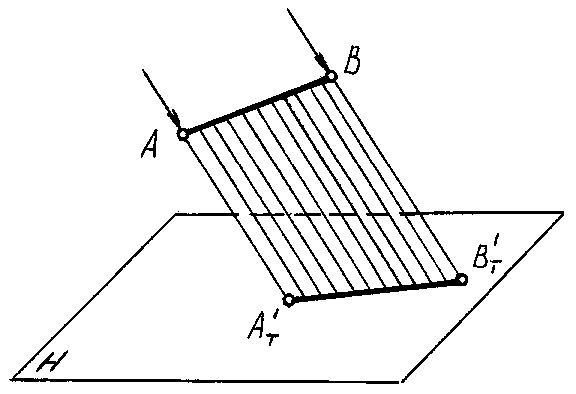
Тень, падающая от прямой линии, состоит из падающих теней от всех ее точек. Лучи, проходящие через все точки прямой, образуют лучевую плоскость, а тень от прямой линии есть линия пересечения лучевой плоскости с плоскостью или поверхностью, на которую падает тень (то есть след лучевой плоскости).

Тенью, падающей от прямой на плоскость, является прямая линия, поэтому для ее построения достаточно построить тени от двух точек, принадлежащих этой прямой.

Тени от точек А и B в этом примере падают на одну плоскость проекций V, поэтому для построения тени отрезка АВ достаточно соединить между собой полученные точки АT'' и ВT'' прямой линией.

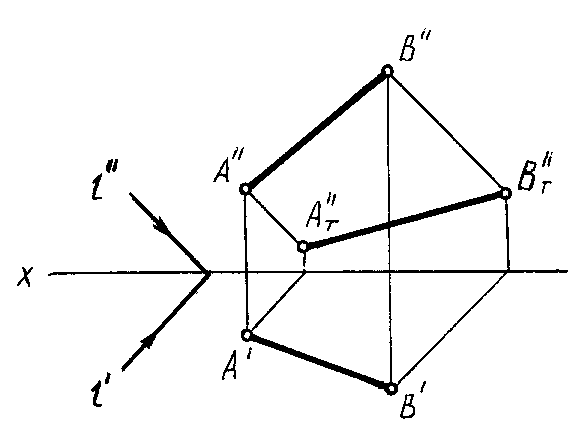
СПОСОБЫ ПОСТРОЕНИЯ ПРИМЕР (РИС.СМ.НИЖЕ):

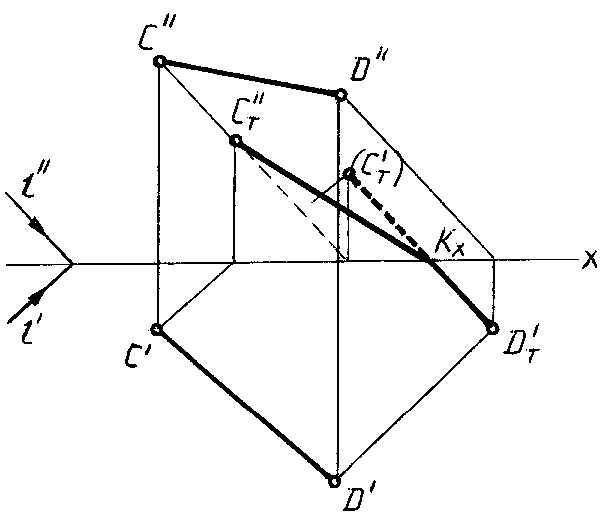
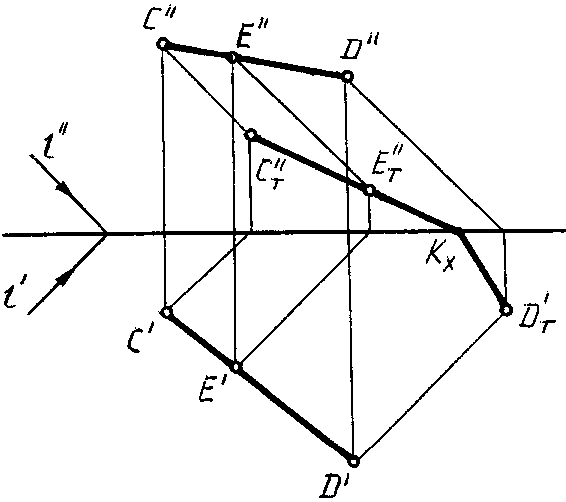
Решение. Тень от отрезка СD падает на две плоскости проекций и представляет собой ломаную линию CT''KXDT'. Точку перелома КX можно определить двумя способами:

1) при помощи мнимой тени (рис.выше)

Для этого строят тень отрезка на одну из плоскостей проекций, предполагая, что второй не существует. На рисунке сначала построена тень отрезка на плоскость Н (СT'DT'). Построенная тень пересекает ось ОХв точке КX, в этой точке тень переломится и с одной плоскости перейдет на другую (в точку СT'').

2.  при помощи тени от промежуточной точки (рис.ниже)

На чертеже точка перелома КX определяется при помощи тени от произвольной промежуточной точкиЕ (ЕT'').

2. Тени плоских фигур в ортогональных проекциях.

ТЕНЬ ОТ ПЛОСКОЙ ФИГУРЫ (непрозрачной пластинки)

Чтобы построить падающую тень от плоской фигуры, ограниченной многоугольником, достаточно построить тени, падающие от всех сторон многоугольника.

На рисунке построена тень, падающая от треугольника АВС на плоскости проекций H и V. Тень от вершины А падает на плоскость V, а от вершины В и вершины С— на плоскость Н. Следовательно, тень от стороны ВС падает на одну плоскость Н и представляет прямую линию, а тени от сторон АВ и АС падают на две плоскости и представляют ломаные линии.

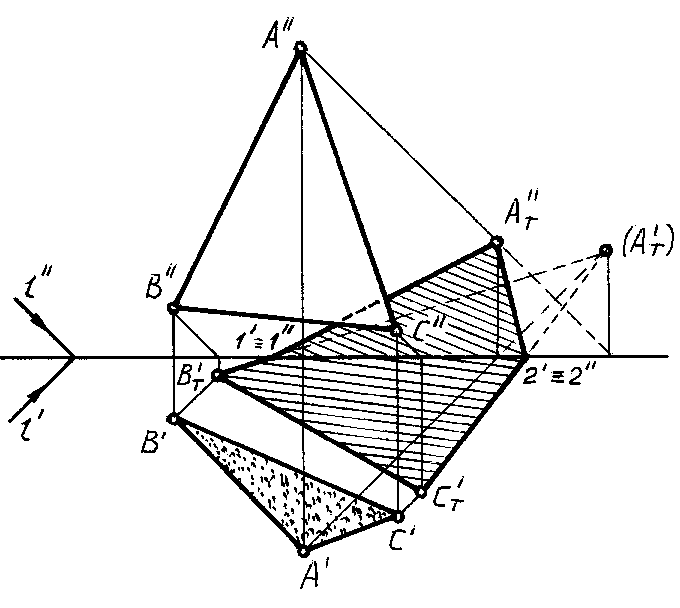
Падающие тени от сторон АВ иАС можно построить при помощи промежуточных точек или при помощи мнимой тени (АT'), падающей от точки А на заднюю полуплоскость Н. Получив треугольник А_THВ_THС_TH, определяем на оси ОХ точки перелома 1 и 2 падающей тени и соединяем их с действительной тенью А_TV от точки А на плоскости V. Сторона плоской фигуры, обращенная к теневому столбу, находится в тени, то есть у плоских фигур следует различать освещенную и неосвещенную стороны. Иначе говоря, плоская фигура всегда имеет собственную тень.