МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра САПР

ОТЧЕТ

по лабораторной работе №1

по дисциплине «Компьютерная графика»

Тема: ПРЕДСТАВЛЕНИЕ И КОМБИНИРОВАННЫЕ ПРЕОБРАЗОВАНИЯ ПЛОСКИХ И ОБЪЕМНЫХ ИЗОБРАЖЕНИЙ

Преподаватель

Колев Г. Ю.

Санкт-Петербург

2024

Цель работы

Исследование математических методов представления и преобразования графических объектов на плоскости и в пространстве.

Задание (вариант 9)

Сформировать отрезок, проведенный из произвольно расположенной точки на плоскости к заданной окружности, определив предварительно координаты точки касания. Необходимо предусмотреть возможность редактирования положения точки и параметры окружности.

Основные сведения:

Для построения отрезка P₁P₂, проведённого из произвольно заданной точки P₁ к заданной окружности с центром в P₀ и радиусом r, необходимо две точки. Координаты первой точки P₁ вводит пользователь, вторая точка P₂ - точка касания, координаты, которой необходимо вычислить. Визуализация задачи представлена на рисунке 1.

Рисунок 1

Рассмотрим . Он прямоугольный, т.к. радиус, проведённый к точке касания, образует прямой угол с касательной.

Длину гипотенузы посчитаем по формуле евклидова расстояния:

Опишем вокруг треугольника окружность. Центр этой окружности будет лежать на середине гипотенузы , т.к. вписанный угол равен половине дуги, на которую он опирается. Таким образом:

Рисунок 2

Тогда точка касания - точка пересечения двух окружностей. Проведём прямую, соединяющую две точки касания.

Рисунок 3

Рассмотрим два прямоугольных треугольника с общим катетом P₂P₃ и обозначим его h.

По теореме Пифагора: и

Т.к. , то:

Тогда можно вычислить h:

Найдём координаты точки :

Тогда можно найти координаты точек касания

Результаты выполнения программы

Для выполнения задания был выбран язык программирования Python и внешняя библиотека PyQT для создания оконного приложения.

Рисунок 1. Интерфейс программы

Все координаты вводятся в текстовые поля. После нажатия кнопки “Начать” на экране сразу появляются окружность, точка и два отрезка, являющиеся касательными к окружности. Произвольная точка и две точки касания выделяются красным цветом. Программа предусматривает случаи, когда выбранная точка совпадает с точкой касания и когда она попадает в саму окружность.

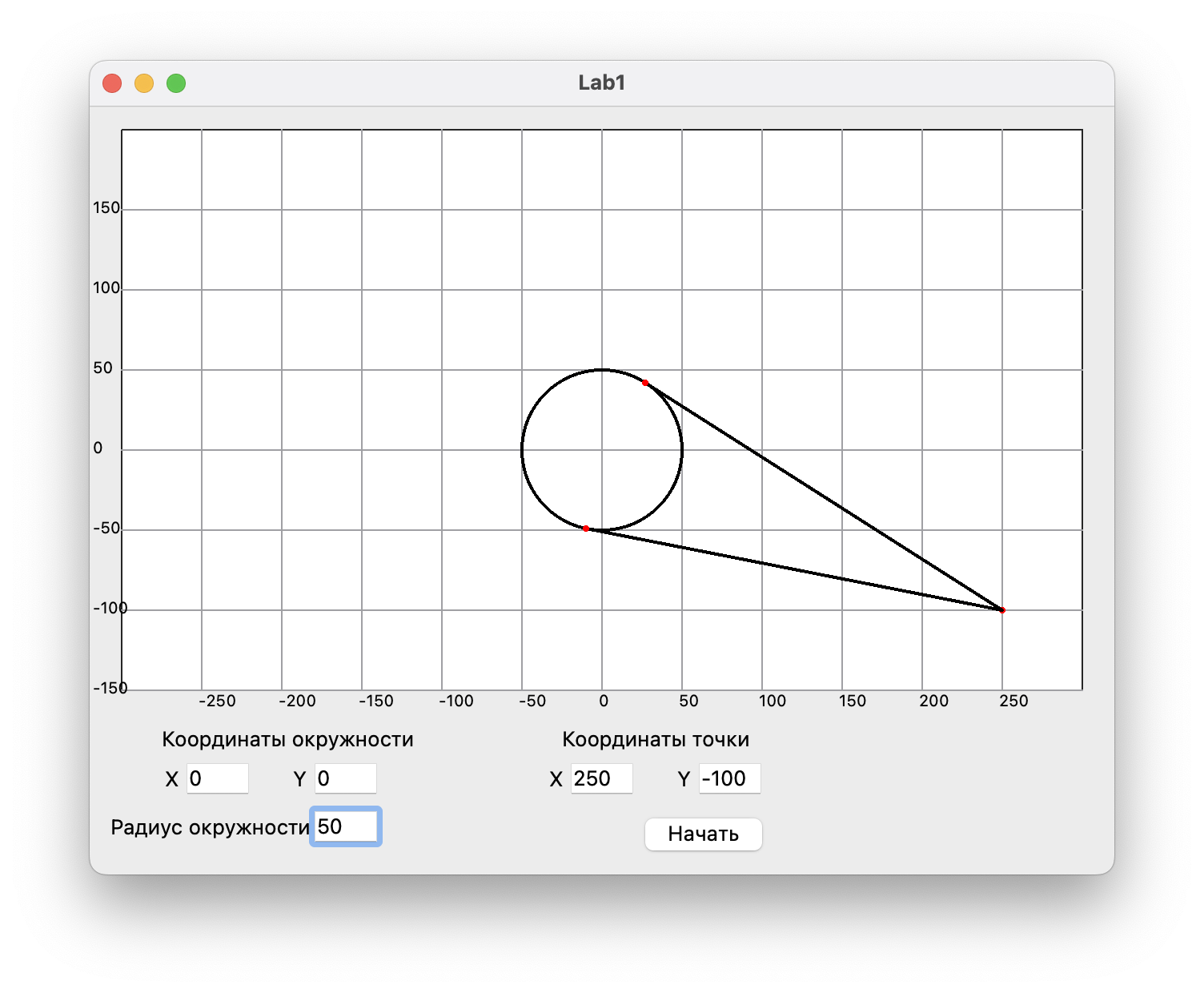
Рисунок 2. Окружность с двумя касательными

Рисунок 3. Окружность с одной точкой касания

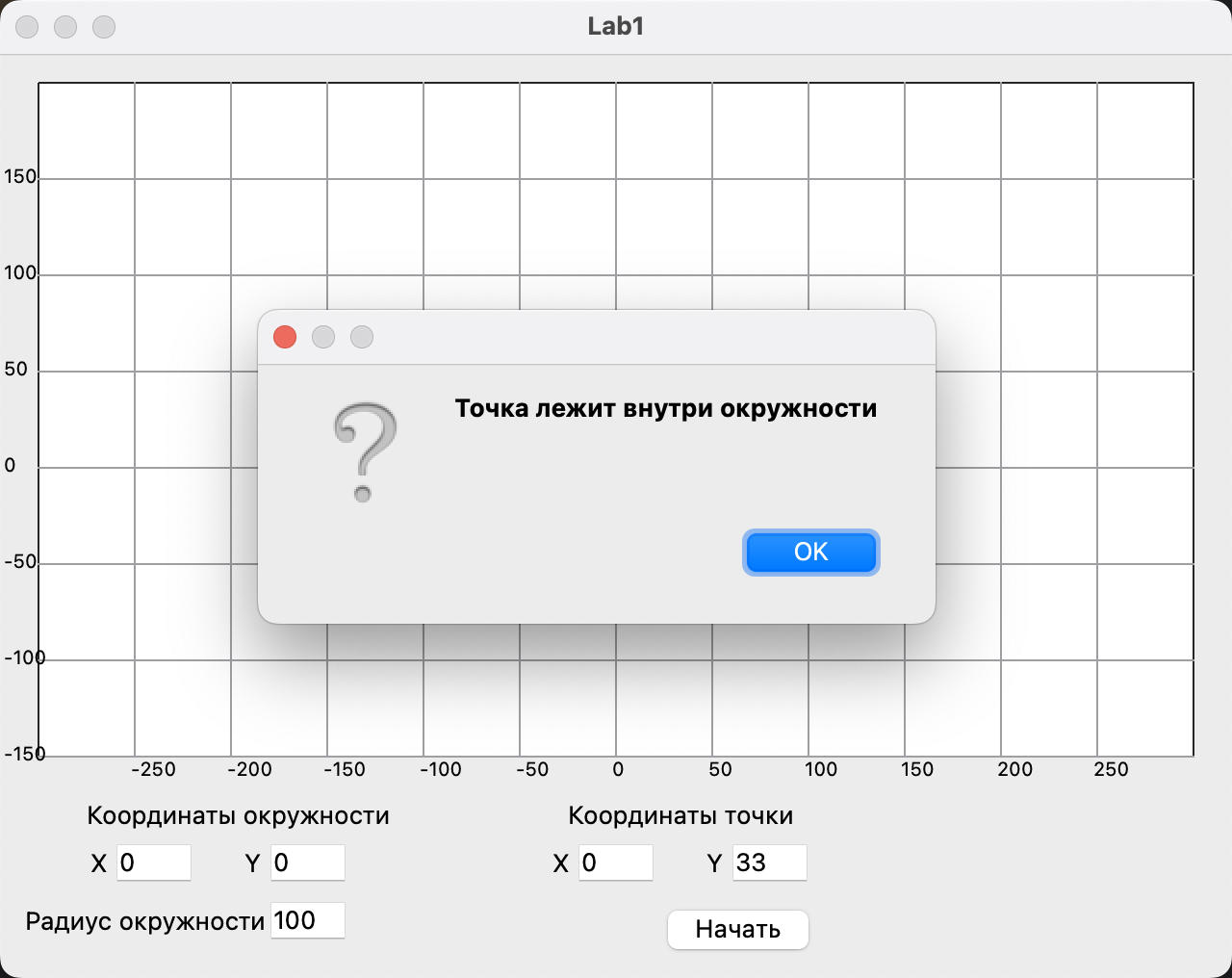
Рисунок 4. Вывод сообщения об ошибке

Вывод

В результате выполнения работы было проведено исследование математических методов представления и преобразования графических объектов на плоскости и в пространстве. Была реализована программа для применения полученных методов на практике.

Приложение

Файл main.py:

import sys

from math import sqrt

from PyQt5.QtCore import Qt, pyqtSlot

from PyQt5.QtWidgets import QApplication, QWidget, QPushButton, QDesktopWidget, QLineEdit, QMessageBox

from PyQt5.QtGui import QPainter, QColor, QPen, QFont, QBrush

x_border = 20 + 300

y_border = 365 - 150

def compute_distance(x1, y1, x2, y2):

return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)

def compute_touchpoints(x0, y0, r0, x1, y1, l):

midx, midy = (x0 + x1) / 2, (y0 + y1) / 2

d, r1 = compute_distance(x0, y0, midx, midy), l / 2

a = (r0 ** 2 - r1 ** 2 + d ** 2) / (2 * d)

h = sqrt(r0 ** 2 - a ** 2)

x2 = x0 + a * (midx - x0) / d

y2 = y0 + a * (midy - y0) / d

x3 = x2 + h * (midy - y0) / d

y3 = y2 - h * (midx - x0) / d

x4 = x2 - h * (midy - y0) / d

y4 = y2 + h * (midx - x0) / d

return x3, y3, x4, y4

class Example(QWidget):

def __init__(self):

super().__init__()

self.lib = {'x': None, 'y': None, 'x_r': None, 'y_r': None, 'r': None,

'x_tch1': None, 'y_tch1': None, 'x_tch2': None, 'y_tch2': None}

self.initUI()

def initUI(self):

self.resize(640, 480)

self.center()

self.setWindowTitle('Lab1')

self.draw_inputs()

self.show()

def center(self):

qr = self.frameGeometry()

cp = QDesktopWidget().availableGeometry().center()

qr.moveCenter(cp)

self.move(qr.topLeft())

def paintEvent(self, e):

qp = QPainter()

qp.begin(self)

self.draw_coords(qp)

if None not in self.lib.values():

self.draw_point(self.lib['x'], self.lib['y'], qp, color='red')

self.draw_line(self.lib['x'], self.lib['y'], self.lib['x_tch1'], self.lib['y_tch1'], qp)

self.draw_line(self.lib['x'], self.lib['y'], self.lib['x_tch2'], self.lib['y_tch2'], qp)

self.draw_cirle(self.lib['x_r'], self.lib['y_r'], self.lib['r'], qp)

self.draw_point(self.lib['x_tch1'], self.lib['y_tch1'], qp, color='red')

self.draw_point(self.lib['x_tch2'], self.lib['y_tch2'], qp, color='red')

self.render_text(qp)

qp.end()

def draw_point(self, x, y, qp, color='black'):

pen = QPen(QColor(color), 4, Qt.SolidLine, Qt.RoundCap)

qp.setPen(pen)

qp.drawPoint(x_border + x, y_border - y)

def draw_line(self, x1, y1, x2, y2, qp):

pen = QPen(Qt.black, 2, Qt.SolidLine, Qt.RoundCap)

qp.setPen(pen)

qp.drawLine(x_border + x1, y_border - y1, x_border + x2, y_border - y2)

def draw_cirle(self, x, y, r, qp):

pen = QPen(Qt.black, 2, Qt.SolidLine, Qt.RoundCap)

qp.setPen(pen)

qp.setBrush(QBrush(Qt.transparent, Qt.SolidPattern))

qp.drawEllipse(x_border + x - r, y_border - y - r, r * 2, r * 2)

def draw_coords(self, qp):

qp.setBrush(QColor(255, 255, 255))

qp.drawRect(20, 15, 600, 350)

pen = QPen(Qt.gray, 1, Qt.SolidLine)

qp.setPen(pen)

for x in range(65, 375, 50):

qp.setPen(pen)

qp.drawLine(20, x, 620, x)

qp.setPen(Qt.black)

qp.setFont(QFont('Decorative', 10))

qp.drawText(2, x + 2, f'{365 - x - 150}')

for y in range(70, 620, 50):

qp.setPen(pen)

qp.drawLine(y, 15, y, 365)

qp.setPen(Qt.black)

qp.setFont(QFont('Decorative', 10))

qp.drawText(y - 2, 375, f'{y - 20 - 300}')

def render_text(self, qp):

qp.setPen(Qt.black)

qp.setFont(QFont('Decorative', 13))

qp.drawText(45, 400, "Координаты окружности")

qp.drawText(47, 425, "X")

qp.drawText(127, 425, "Y")

qp.drawText(13, 455, "Радиус окружности")

qp.drawText(295, 400, "Координаты точки")

qp.drawText(287, 425, "X")

qp.drawText(367, 425, "Y")

def draw_inputs(self):

self.input_x_r = QLineEdit(self)

self.input_x_r.move(60, 410)

self.input_x_r.resize(40, 20)

self.input_y_r = QLineEdit(self)

self.input_y_r.move(140, 410)

self.input_y_r.resize(40, 20)

self.input_r = QLineEdit(self)

self.input_r.move(140, 440)

self.input_r.resize(40, 20)

self.input_x = QLineEdit(self)

self.input_x.move(300, 410)

self.input_x.resize(40, 20)

self.input_y = QLineEdit(self)

self.input_y.move(380, 410)

self.input_y.resize(40, 20)

# Create a button in the window

self.button = QPushButton('Начать', self)

self.button.move(340, 440)

# connect button to function on_click

self.button.clicked.connect(self.on_click)

self.show()

@pyqtSlot()

def on_click(self):

self.lib['x_r'] = int(self.input_x_r.text()) # x_r

self.lib['y_r'] = int(self.input_y_r.text()) # y_r

self.lib['r'] = int(self.input_r.text()) # r

self.lib['x'] = int(self.input_x.text()) # x

self.lib['y'] = int(self.input_y.text()) # y

l = compute_distance(self.lib['x_r'], self.lib['y_r'], self.lib['x'],

self.lib['y']) # distance between point and circle

if l < self.lib['r']:

QMessageBox.question(self, 'Message', "Точка лежит внутри окружности", QMessageBox.Ok,

QMessageBox.Ok)

self.lib['r'] = None

elif l == self.lib['r']:

self.lib['x_tch1'] = self.lib['x']

self.lib['y_tch1'] = self.lib['y']

self.lib['x_tch2'] = self.lib['x']

self.lib['y_tch2'] = self.lib['y']

self.update()

else:

x3, y3, x4, y4 = compute_touchpoints(self.lib['x_r'], self.lib['y_r'], self.lib['r'],

self.lib['x'], self.lib['y'], l)

self.lib['x_tch1'] = round(x3) # 1st touchpoint x

self.lib['y_tch1'] = round(y3) # 1st touchpoint y

self.lib['x_tch2'] = round(x4) # 2nd touchpoint x

self.lib['y_tch2'] = round(y4) # 2nd touchpoint y

self.update()

if __name__ == '__main__':

app = QApplication(sys.argv)

ex = Example()

sys.exit(app.exec_())