МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра вычислительной техники

ОТЧЕТ

по лабораторной работе №2

по дисциплине «Введение в искусственный интеллект»

Тема: Методы информированного (эвристического) поиска

Преподаватель

Родионов С.В.

Санкт-Петербург

2024

Цель работы:

Практическое закрепление теоретических основ информированного (эвристического) поиска.

Постановка задачи:

Реализовать программу поиска пути решения головоломки «8-ка» с использованием эвристических функций h1 (поиск фишек не на своих местах с присваиванием приоритета) и h2 (манхэттенское расстояние) для алгоритма поиска A* двух заданных состояний: целевого и исходного. Экспериментальным путем оценить временную и емкостную сложность решения задачи для двух заданных стратегий.

Описанные выше состояния изображены на рисунке 1 и 2 соответственно.

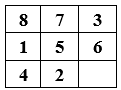
Рисунок 1 – начальное состояние

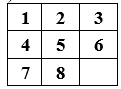
Рисунок 2 – конечное состояние

Распределение обязанностей:

Описание выбранных структур данных:

Для решения поставленной задачи был использован язык Python 3.11. Для реализации программы были реализованы два класса - состояние и вершина дерева.

Структура	Поля	Описание
class Node	self.state	матрица состояний
	self.x	“x” координата пустой клетки в матрице
	self.y	“y” координата пустой клетки в матрице
	self.iter	расстояние между текущим и исходным состоянием (глубина дерева)
	self.unique	параметр, указывающий на уникальность матрицы состояния данного узла в дереве, принимает значения: “0” - не уникальное, “1” - уникальное.
	self.action	действие, которое привело к текущему состоянию
class TreeNode	self.data	состояние, записанное в узле
	self.children	дочерние узлы
	self.parent	родительский узел
	self.h	словарь, хранящий значения эвристических функций (значение h1 по ключу 1, значение h2 по ключу 2)
states: Dict		хэш-таблица, хранящая посещенные узлы (состояния матрицы)

Описание методов класса Node:

Метод	Описание
__init__(self)	метод инициализации класса
perform_action(self, action: str)	меняет матрицу состояний в соответствии с выбранным действием (up, down, left, right)
out_node(self)	выводит матрицу состояний
get_string(self)	возвращает матрицу состояний в виде последовательного набора чисел
available_actions(self)	выводит возможные действия игры для данного узла

Описание методов класса TreeNode:

Метод	Описание
__init__(self, data: Node, parent)	Метод инициализации класса
add_child(self, child_node)	Добавление дочернего узла в список children, содержащий дочерние вершины выбранного узла
get_node(self)	Получение объекта состояния, записанного в данном узле
count_h1(self)	Подсчет эвристической функции h1 (количество фишек, стоящих не на своих местах)
count_h2(self)	Подсчет эвристической функции h2 (суммарное манхэттенское расстояние по всем фишкам до целевого положения)

Описание алгоритма поиска a*:

Поиск А* - наиболее широко известная разновидность поиска по первому наилучшему совпадению. В нем применяется оценка узлов, объединяющая в себе эвристическую функцию (стоимость прохождения от данного узла до цели) h(n) и стоимость достижения данного узла g(n):

Поскольку функция g(n) позволяет определить стоимость пути от начального узла до узла n, а функция h(n) определяет оценку стоимости наименее дорогостоящего пути от узла n до цели, то справедливо, что f(n) - это оценка стоимости наименее дорогостоящего пути решения, проходящего через узел n.

Таким образом, при при переходе к потомкам узла, проверяется узел с наименьшим значением g(n) + h(n).

Реализация поиска A* похожа на реализацию алгоритмов слепого поиска с тем отличием, что при переходе к новой раскрываемой вершине мы выбираем не узел из начала очереди или из конца дека, а берем тот узел, значение эвристической функции которого минимально.

Пример работы программы:

Программа представляет из себя меню с выбором одной из двух эвристических функций. При выборе функции программа первым делом спрашивает, необходимо ли выводить поиск решения пошагово, после чего производит поиск решения. На каждом шаге отображается текущий состояние поля текущего раскрываемого узла, значение его эвристической функции, а также узлы, найденные на этом шаге со следующей информацией: какое действие было сделано для раскрытия данной вершины, состояние поля, значение эвристической функции и уникальность данного состояния. В любой момент пошаговое выполнение можно прервать и перейти к результату. Результат включает в себя количество шагов, количество найденных за время поиска состояний, глубину, на которой было найдено решение, и время, в течение которого алгоритм работал.

Рисунок 3 - меню выбора алгоритма поиска.

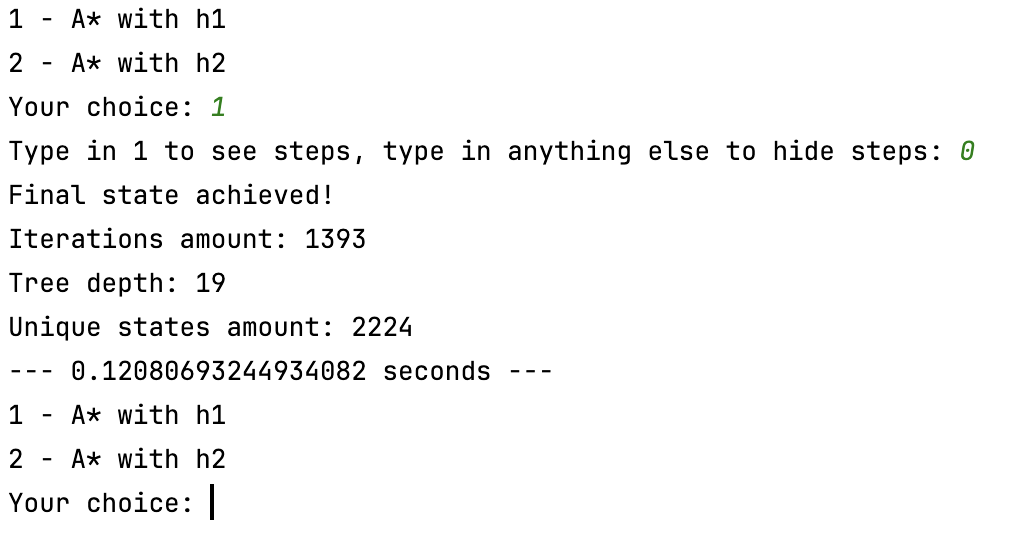
Рисунок 4 - результаты выполнения алгоритма поиска без пошагового выполнения (эвристическая функция h1)

Рисунок 5 - пошаговый режим программы (h2)

Рисунок 5 - завершение пошагового режима (h2)

Оценки временной и ёмкостной сложности алгоритмов:

	Поиск в ширину	Поиск с итеративным углублением	Алгоритм A* с эвристикой h1	Алгоритм A* с эвристикой h2
Временная сложность (кол-во шагов)	14461	14461	1393	257
Ёмкостная сложность (кол-во уникальных вершин в дереве поиска)	22892	3426	2224	426

В результате выполнения экспериментальных запусков программы в разных версиях было обнаружено, что сложность алгоритмов эвристического поиска меньше, чем сложность алгоритмов слепого поиска. При этом при использовании эвристики h2 (манхэттенское расстояние) алгоритм имеет меньшую как временную, так и ёмкостную сложность по сравнению с использованием эвристики h1 (поиск фишек не на своих местах с присваиванием приоритета).

Вывод

В результате выполнения лабораторной работы были закреплены навыки по обходу графа алгоритмами информированного поиска. Был изучен и реализован алгоритм А* для поиска оптимального решения в игре “восьмерка”. При сравнении алгоритма A* с алгоритмами слепого поиска в ширину и глубину было замечено уменьшение временной сложности алгоритма примерно в 10 раз, а при использовании эвристики h2 программе поиска потребовалось всего 257 итераций для нахождения решения. Емкостная сложность также уменьшилась. В итоге, можно сказать, что если алгоритм эвристического поиска применим к решению задачи, он будет более эффективным, чем алгоритм слепого поиска.