лаб1

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра вычислительной техники

ОТЧЕТ

по лабораторной работе №1

по дисциплине «Введение в искусственный интеллект»

Тема: Методы неинформированного (слепого) поиска

Преподаватель

Родионов С.В.

Санкт-Петербург

2024

Цель работы:

Практическое закрепление понимания общих идей поиска в пространстве состояний и стратегий слепого поиска.

Постановка задачи:

Реализовать программу поиска пути решения головоломки «8-ка» с использованием алгоритма поиска в ширину и итеративного алгоритма поиска в глубину – для двух заданных состояний: целевого и исходного. Экспериментальным путем оценить временную и емкостную сложность решения задачи для двух заданных стратегий.

Описанные выше состояния изображены на рисунке 1 и 2 соответственно.

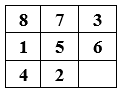
Рисунок 1 – начальное состояние

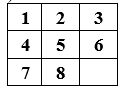
Рисунок 2 – конечное состояние

Распределение обязанностей:

Описание выбранных структур данных:

Для решения поставленной задачи был использован язык Python 3.11. Для реализации программы были реализованы два класса - состояние и вершина дерева.

Структура	Поля	Описание
class Node	self.state	матрица состояний
	self.x	“x” координата пустой клетки в матрице
	self.y	“y” координата пустой клетки в матрице
	self.iter	расстояние между текущим и исходным состоянием (глубина дерева)
	self.unique	параметр, указывающий на уникальность матрицы состояния данного узла в дереве, принимает значения: “0” - не уникальное, “1” - уникальное.
class TreeNode	self.data	состояние, записанное в узле
	self.children	дочерние узлы
	self.parent	родительский узел
states: Dict		хэш-таблица, хранящая посещенные узлы (состояния матрицы)

Описание методов класса Node:

Метод	Описание
__init__(self)	метод инициализации класса
perform_action(self, action: str)	меняет матрицу состояний в соответствии с выбранным действием (up, down, left, right)
out_node(self)	выводит матрицу состояний
get_string(self)	возвращает матрицу состояний в виде последовательного набора чисел
available_actions(self)	выводит возможные действия игры для данного узла

Описание методов класса TreeNode:

Метод	Описание
__init__(self, data: Node, parent)	Метод инициализации класса
add_child(self, child_node)	Добавление дочернего узла в список children, содержащий дочерние вершины выбранного узла
get_node(self)	Получение объекта состояния, записанного в данном узле

Описание алгоритмов:

Алгоритм поиска в ширину:

Поиск в ширину - это простая стратегия, в которой вначале развертывается корневой узел, затем - все преемники корневого узла, после этого развертываются преемники этих преемников и т.д. Вообще говоря, при поиске в ширину, прежде чем происходит развертывание каких-либо узлов на следующем уровне, развертываются все узлы на данной конкретной глубине в дереве поиска.

Алгоритм поиска с итеративным углублением:

Поиск с итеративным углублением – это стратегия поиска, которая объединяет в себе преимущества поиска в глубину и в ширину. Этот метод позволяет выполнять поиск в глубину с постепенным увеличением глубины, что позволяет сбалансировать эффективность и потребление ресурсов.

Поиск в глубину – это алгоритм обхода графа или дерева, который начинает с начальной вершины и идет по одной из ветвей как можно глубже, пока не достигнет конечной вершины или не обнаружит, что больше нет вершин для посещения. Если путь не приводит к решению, алгоритм возвращается к предыдущей вершине и исследует другие направления.

Процесс поиска с итеративным углублением начинается с минимальной глубины, обычно с глубины 1. На каждой итерации выполняется поиск в глубину с ограничением на максимальную глубину. Если цель не найдена на текущей глубине, максимальная глубина увеличивается, и поиск начинается заново. Этот процесс повторяется до тех пор, пока цель не будет найдена или пока не будет достигнута максимальная глубина, заданная пользователем.

Реализуется с помощью надстройки над алгоритмом поиска в глубину с ограничением в виде цикла, инкрементирующего ограничивающую глубину дерева при отсутствии результата на текущей итерации. Поиск в глубину реализуется с помощью стека и заключается в следующем: после раскрытия очередной вершины все её потомки поочерёдно проверяются на соответствие конечному результату или повторному состоянию и помещаются в стек, если не являются таковыми, далее из стека достается верхний элемент и алгоритм повторяется (до того момента пока в стеке либо не останется ни одной вершины, либо не будет найдено искомое состояние, либо не достигнут предел глубины).

Пример работы программы:

Программа представляет из себя меню с выбором одного из двух алгоритмов поиска. При выборе алгоритма программа производит поиск решения, после чего отображает его результаты - количество шагов, найденных за время поиска состояний и глубину, на которой было найдено решение. После этого можно посмотреть по шагам найденный путь решения задачи от исходного состояния до целевого. Запуск алгоритмов можно повторять несколько раз подряд в разном порядке.

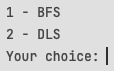
Рисунок 3 - меню выбора алгоритма поиска.

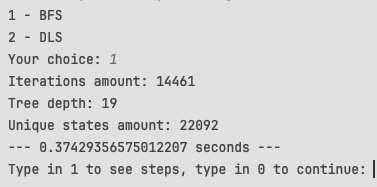
Рисунок 4 - результаты выполнения алгоритма поиска.

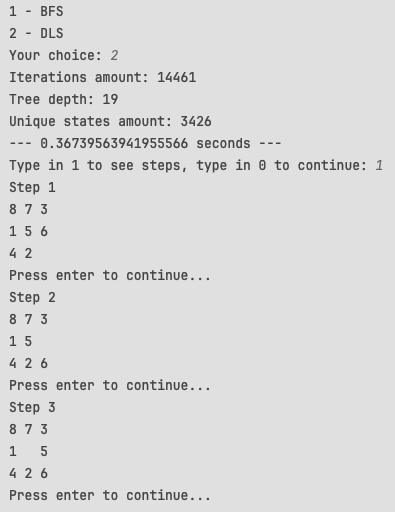
Рисунок 5 - пошаговый режим программы

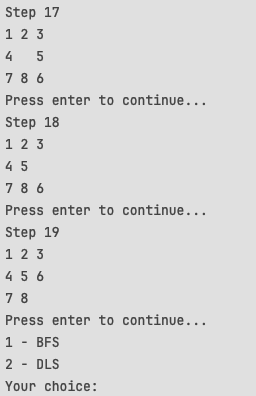
Рисунок 5 - завершение пошагового режима

Оценки временной и ёмкостной сложности алгоритмов:

	Поиск в ширину	Поиск с итеративным углублением
Временная сложность (кол-во шагов)	14461	14461
Ёмкостная сложность (кол-во уникальных вершин в дереве поиска)	22892	3426

В результате выполнения экспериментальных запусков программы в разных версиях было обнаружено, что сложность обоих алгоритмов колеблется в зависимости от того, в каком порядке выполняются действия в игре “Восьмерка”. Также порядок выполнения действий влияет на то, на какой глубине при итеративном поиске будет найдено целевое решение. Общий вывод из оценки временной и емкостной сложности заключается в том, что поиск в ширину имеет меньшую временную сложность, а поиск с итеративным углублением может иметь как большую емкостную сложность при большой глубине дерева так и меньшую, поскольку после достижения определенной глубины прошлое дерево удаляется и создается новое и нужно смотреть только на глубину финального дерева.

Вывод:

В результате выполнения работы было успешно закреплено понимание общих идей поиска в пространстве состояний и стратегий слепого поиска. Была реализована программа, производящая поиск решений в игре “Восьмерка” на основе двух подходов: поиск в ширину и поиск с итеративным углублением. Сравнение двух подходов показало, что в данной задаче лучше использовать поиск в ширину, поскольку на его выполнение требуется меньше времени и сам результат вне зависимости от порядка выполнения действий в игре всегда выявляется на наименьшей возможной глубине дерева.

В ходе выполнения работы был выбран подход ООП для реализации структур данных для работы с деревом состояний и подходы к реализации алгоритмов поиска. Так, например, в ходе разработки алгоритма поиска в глубину было принято решения отказаться от рекурсивного подхода в пользу реализации алгоритма с помощью стека.

Исходный код:

import time

from copy import deepcopy

class Node:

def __init__(self):

self.state = \

[['8', '7', '3'],

['1', '5', '6'],

['4', '2', ' ']]

self.x = 2

self.y = 2

self.iter = 1

self.unique = 1

states.update({self.get_string(): self.iter})

def perform_action(self, action: str):

if action == 'right':

self.state[self.x][self.y] = self.state[self.x][self.y - 1]

self.state[self.x][self.y - 1] = ' '

self.y -= 1

elif action == 'left':

self.state[self.x][self.y] = self.state[self.x][self.y + 1]

self.state[self.x][self.y + 1] = ' '

self.y += 1

elif action == 'up':

self.state[self.x][self.y] = self.state[self.x + 1][self.y]

self.state[self.x + 1][self.y] = ' '

self.x += 1

elif action == 'down':

self.state[self.x][self.y] = self.state[self.x - 1][self.y]

self.state[self.x - 1][self.y] = ' '

self.x -= 1

self.iter += 1

if self.get_string() not in states.keys():

states.update({self.get_string(): self.iter})

else:

self.unique = 0

def out_node(self):

for i in range(len(self.state)):

print(*self.state[i])

def get_string(self) -> str:

s = ''

for i in range(len(self.state)):

s += ''.join(self.state[i])

return s

def available_actions(self) -> list:

actions = []

if 0 <= self.x <= 1:

actions += ['up']

if 1 <= self.x <= 2:

actions += ['down']

if 1 <= self.y <= 2:

actions += ['right']

if 0 <= self.y <= 1:

actions += ['left']

return actions

class TreeNode:

def __init__(self, data: Node, parent):

self.data = data

self.children = []

self.parent = parent

def add_child(self, child_node):

self.children.append(child_node)

def get_node(self):

return self.data

def BFS():

root = TreeNode(Node(), None)

states.clear()

fifo = [root]

it = 0

while fifo:

return new_tree_node

fifo.append(new_tree_node)

def DLS(limit: int, it: int):

root = TreeNode(Node(), None)

states.clear()

stack = [root]

while stack:

it += 1

current_node = stack.pop()

actions = current_node.get_node().available_actions()

for action in actions:

new_node = deepcopy(current_node.get_node())

new_node.perform_action(action)

if new_node.unique:

new_tree_node = TreeNode(new_node, current_node)

current_node.add_child(new_tree_node)

if new_tree_node.get_node().get_string() == looked_node:

print(f"Iterations amount: {it}")

print(f"Tree depth: {new_tree_node.get_node().iter}")

print(f"Unique states amount: {len(states)}")

return new_tree_node, it

elif new_tree_node.get_node().iter <= limit:

stack.append(new_tree_node)

return None, it

def IDS():

i = 0

it = 0

while True:

# print(f"iteration {i}")

current_node, it = DLS(i, it)

if current_node:

return current_node

i += 1

def show_steps(final_node: TreeNode):

steps = {}

current_node = final_node

while current_node is not None:

steps.update({current_node.get_node().iter: current_node.get_node()})

current_node = current_node.parent

for i in range(1, final_node.get_node().iter + 1):

print(f"Step {i}")

steps[i].out_node()

input("Press enter to continue...")

states = {}

looked_node = '12345678 '

mode = -1

while mode != 0:

mode = input('''1 - BFS

2 - DLS

Your choice: ''')

if mode == "1":

start_time = time.time()

result = BFS()

print("--- %s seconds ---" % (time.time() - start_time))

elif mode == "2":

start_time = time.time()

result = IDS()

print("--- %s seconds ---" % (time.time() - start_time))

else:

break

steps = input("Type in 1 to see steps, type in 0 to continue: ")

if steps == "1":

show_steps(result) it += 1

current_node = fifo.pop(0)

actions = current_node.get_node().available_actions()

for action in actions:

new_node = deepcopy(current_node.get_node())

new_node.perform_action(action)

if new_node.unique:

new_tree_node = TreeNode(new_node, current_node)

current_node.add_child(new_tree_node)

if new_tree_node.get_node().get_string() == looked_node:

print(f"Iterations amount: {it}")

print(f"Tree depth: {new_tree_node.get_node().iter}")

print(f"Unique states amount: {len(states)}")