
Mechanics-11
.pdfМинистерство образования и науки Российской Федерации Ярославский государственный университет
им. П. Г. Демидова
В.П. Алексеев, Е. О. Неменко,
В.А. Папорков, Е. В. Рыбникова
Лабораторная работа № 11
Определение момента инерции тел методом трифилярного подвеса.
Ярославль 2013
Лабораторная работа № 11.
Определение момента инерции тел методом трифилярного подвеса1
Цель работы:
•изучение метода трифилярного подвеса для определения моментов инерции тел;
•экспериментальное определение этим методом моментов инерции некоторых тел;
•проверка теоремы о переносе осей моментов инерции.
Оборудование:
•платформа на трифилярном подвесе;
•секундомер (или электронный счётчик);
•линейка;
•тела (грузы) для измерения момента инерции.
11.1. Краткая теория
В простых случаях величину момента инерции можно определять расчетом, а в сложных – его приходится находить экспериментально.
Одним из способов нахождения моментов инерции твердого тела является метод крутильных колебаний. Метод трифилярного подвеса – его частный случай.
11.1.1. Проверка теоремы о переносе осей моментов инерции
Вращение твердого тела с динамической точки зрения вызывает необходимость введения весьма важных новых понятий. Так, наряду с понятием о силах вводиться понятие о моментах сил и наряду с понятием о массе – понятие о моменте инерции.
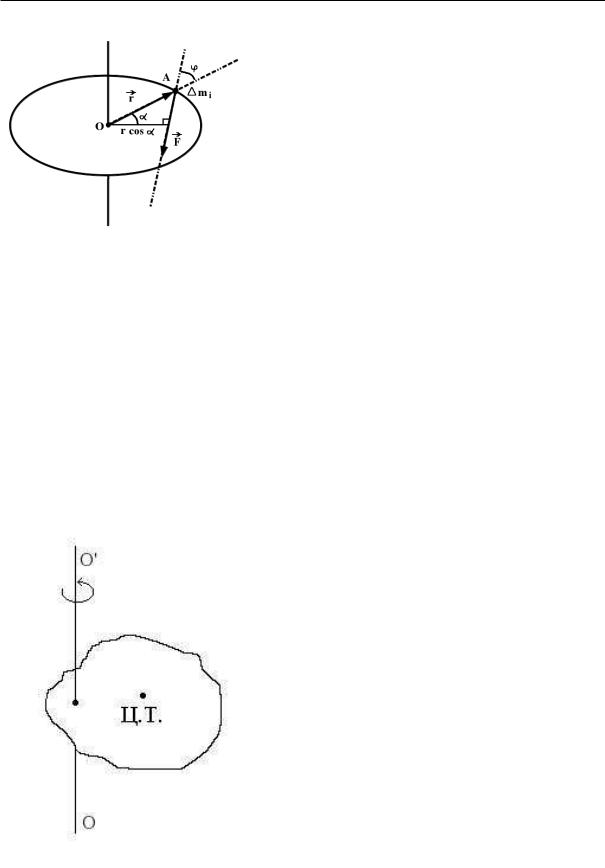
Рассмотрим движение одной материальной точки A с массой m, удерживаемой на окружности
радиуса r с помощью какой – либо связи (рис. 11.1). |
|
|
Пусть на точку a действует постоянная по величине сила |
~ |
~ |
F . Вектор M |
= (~r × F ) называется |
|
~ |
|
|
моментом силы F относительно точки O. Его модуль |
|
|
~ |
|
(11.1) |
|M| = rF sin ϕ = rF cos α, |
|
|
численно равен произведению величины силы F на длину перпендикуляра, опущенного на направле- |
||
~ |
относительно |
|
ние силы из точки O (центра вращения). Расстояние r cos α называется плечом силы F |
||
точки O |
|
|
|
|
|
1Ранее данная работа имела номер 8. |
|
|
1
2
Величина J = mr2, численно равная произведению массы m точки A на квадрат ее расстояния оси вращения, называется моментом инерции точки A относительно оси.
Нетрудно убедиться в том, что основной закон динамики для вращательного движения записывается в виде:
M = J |
dω |
, |
(11.2) |
|
dt |
||||
|
|
|
Угловое ускорение, приобретаемое при вращении вокруг некоторого центра, прямо пропорционально моменту силы, действующему на точку, и обратно пропорционально моменту инерции материальной точки.
Рассмотрим теперь вращение твердого тела около некоторой неподвижной оси OO′ (рис. 11.2).
Если выше мы говорили о моменте силы относительно точки (центра вращения), то здесь для характеристики способности силы F вызывать вращение вокруг данной
оси вводится понятие о моменте сил относительно оси.
Очевидно, что момент силы относительно оси создается только той составляющей силы, которая лежит в плоскости перпендикулярной оси.
Выделим малый элемент в твердом теле с массой mi и будем рассматривать только ту состав-
ляющую действующей на него силы, которая лежит в плоскости, перпендикулярной к оси вращения OO′. Обозначим эту составляющую силы через Fi. Пусть сила Fi образует угол α с касательной к траектории элемента mi. Угол α считаем острым. Тогда, пользуясь соотношением (11.2), для
этого элемента можно написать равенство:
Mi = Ji |
dωi |
= Jiεi, |
(11.3) |
|
dt |
||||
|
|
|
где εi – угловое ускорение элемента.
Ясно, что такие же равенства мы можем написать для всех прочих элементов. Если же имеем n элементов, на которые разбито наше тело, то получим и n подобных
(11.3) соотношений:
F1r1 cos α1 |
= |
m1r12ε1 |
(для 1 − го элемента) |
F2r2 cos α2 |
= |
m2r22ε2 |
(для 2 − го элемента) |
F3r3 cos α3 |
= |
m3r32ε3 |
(для 3 − го элемента) (11.4) |
F4r4 cos α4 |
= |
m4r42ε4 |
(для 4 − го элемента) |
. . .
Сложим эти равенства и получим:
n |
n |
|
X |
X |
|
Firi cos αi = |
miri2εi, |
(11.5) |
i=1 |
i=1 |
|
где угловое ускорение ε постоянно для всех элементов, поэтому его можно вывести из-под знака суммы, а i = 1, 2, 3, . . . , n.
Величина
n |
|
X |
(11.6) |
M = Firi cos αi |
i=1
Рис. 11.2. Вращение твёрдого тела относительно оси
представляет собой сумму моментов сил, действующих на все элементы твердого тела, т.е. она представляет собой полный момент M сил, действующих на твердое тело.
Величина
|
n |
|
|
X |
|
J = |
miri2, |
(11.7) |
i=1
11.2. Описание экспериментальной установки |
3 |
|
|
равная сумме моментов инерции отдельных элементов, на которые мы разбили тело, называется моментом инерции тела относительно данной оси OO′.
Таким образом, и для твердого тела основной закон динамики вращательного движения можно представить в виде:
M = Jε, |
(11.8) |
где ε – угловое ускорение, приобретаемое твердым телом, прямо пропорционально приложенному моменту сил M и обратно пропорционально моменту инерции J.
На самом деле при определении момента инерции твердого тела (формула 11.7) должны быть взяты бесконечно малые элементы массы. И тогда суммирование заменяется операцией интегрирования:
J = Z |
r2dm. |
(11.9) |
Вводя плотность тела ρ, имеем dm = ρdV , где dV – элемент объема. Если ρ = const, то |
|
|
J = ρ Z |
dV r2. |
(11.10) |
V |
|
|
11.2. Описание экспериментальной установки
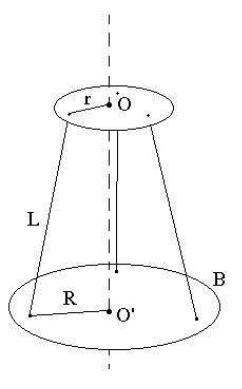
Трифилярный подвес состоит из круглой платформы В, подвешенной на трех симметрично расположенных по вершинам равностороннего треугольника металлических нитей (рис. 11.3). Наверху эти нити также симметрично прикреплены к диску несколько меньшего диаметра, чем диаметр платформы. Диск укреплен на кронштейне
иснабжен рычагом, при помощи которого системе можно сообщать крутильные колебания вокруг вертикальной оси, перпендикулярной к ее плоскости и проходящей через ее середину. Центр масс платформы при этом перемещается по оси вращения. Период колебаний определяется величиной момента инерции платформы. Он будет другим, если платформу нагрузить каким-либо телом, этим
ипользуются в настоящей работе. На платформе расположены 5 центрующих штырей, один в центре, остальные четыре попарно, на двух различных расстояниях от её центра. Грузы устанавливаются на них соответствующим гнездом.
Для определения периода колебаний используется секундомер (или электронный счетчик).
11.2.1. Теория метода
Обозначим длину нитей через L, радиус платформы – R, радиус верхнего диска – r. При повороте платформы на
некоторый угол относительно верхнего диска точка прикрепления нити B переходит в положение B1 и платфор-
Рис. 11.3. Схема трифилярного подвеса ма приподнимается на некоторую высоту h (рис. 11.4):
|
h = OO1 = AC − A1C. |
|||
Это выражение можно записать в виде: |
|
|
||
|
|
(AC)2 |
− (A1C)2 |
|
|
h = |
|
|
(11.11) |
|
|
|
||
|
|
AC |
+ A1C |
|
Из геометрических данных имеем: |
|
|
||
из |
ABC AC2 = BC2 − AB2 = L2 − (R − r)2 |
|||
из A1B1C |
A1C2 = B1C2 − A1B12 = L2 − (R2 + r2 − 2Rr cos α)2 |
|||

11.2. Описание экспериментальной установки |
4 |
|
|
Рис. 11.4. К выводу формулы момента инерции
Тогда: |
|
|
|
|
|
|
|
|
|
h = |
L2 |
− (R − r)2 − [L2 |
(R2 + r2 − 2Rr cos α)] |
||||||
|
|
|
|
|
|
|
|
= |
|
|
|
AC + A1C |
|
||||||
|
|
|
|
|
|||||
|
= |
|
2Rr − 2Rr cos α |
= |
2Rf(1 − cos α) |
, |
|
||
|
|
AC − A1C |
AC − A1C |
|
|||||
|
|
|
|
|
|
||||
|
|
|
h = |
4Rr sin2 α2 |
. |
(11.12) |
|||
|
|
|
|
||||||
|
|
|
|
AC + A1C |
|
|
|||
При большой длине нитей и малых углах отклонения α, синус угла можно заменить просто значением α, а величину знаменателя положить равной 2L, т. к. в этом случае
AC ≈ A1C ≈ L. |
|
||
При этих допущениях получаем: |
|
|
|
h = |
4Rrα2 |
(11.13) |
|
|
. |
||
|
|||
|
2L |
|
|
Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то прираще-
ние потенциальной энергии будет равно
Eп = mgh = mg |
Rrα2 |
(11.14) |
2L , |
где g – ускорение свободного падения.
Вращаясь в другом направлении, платформа придет в положение равновесия с кинетической энергией, равной
Eк = J |
ω2 |
(11.15) |
2 , |
где J – момент инерции платформы, ω – угловая скорость платформы в момент достижения ею
положения равновесия.
На основании закона сохранения механической энергии имеем:
|
|
|
|
1 |
Jω2 |
= mgh, |
|
|
||||
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
πα |
|
|
|
Rrα2 |
|
||||
|
|
J |
|
2 |
|
= mg |
|
, |
(11.16) |
|||
|
2 |
T |
2L |
|||||||||
где T – период полного колебания. |
|
|
|
|
|
|
|
|
|
|
||
Из (11.16) получаем: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
J = |
mgRr |
T 2. |
|
(11.17) |
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
4π2L |
|
|
|||

11.3. Порядок выполнения работы |
5 |
|
|
При выводе формулы (11.17) не учитывались потери энергии на трение. Учет таких потерь весьма затруднителен. Однако поправки оказываются небольшими, если потери энергии за период малы по сравнению с энергией колебаний системы. Таким образом, формула (11.17) справедлива, если
τ T, |
(11.18) |
где τ – время, в течение которого амплитуда колебаний платформы существенно (в 2 – 3 раза)
уменьшается.
По формуле (11.17) может быть определён момент инерции и самой платформы и тела, положенного на неё, т. к. все величины в правой части формулы могут быть непосредственно измерены.
Весьма важной в практическом отношении является теорема Гюйгенса-Штейнера о переносе осей моментов инерции, которая гласит: момент инерции тела, относительно любой оси, равен моменту инерции тела, относительно оси, проходящей через центр тяжести параллельно данной, сложенному с произведением массы на квадрат расстояния между осями:
J = J0 + ma2. |
(11.19) |
11.3. Порядок выполнения работы
1)Сначала определяют J0 – момент инерции ненагруженной платформы. Сообщают диску вращательный импульс, по секундомеру измеряют время t 30-40 колебаний. Находят период одного полного колебания T по формуле:
T = Nt ,
где N – число колебаний. Для уменьшения случайной ошибки, T находят не менее 5 раз и для расчета берут Tср. Величины L, r и R измеряют линейкой. Затем по формуле (11.17) вычисляют J.
2)Определяют момент инерции платформы с одним грузом массы m, расположенным в её цен-
тре. Вновь сообщая платформе колебания, тем же способом определяют их период. По формуле (11.17) вычисляют значения момента инерции нагруженной платформы, при этом масса нагруженной платформы равна сумме масс диска платформы и груза. Момент инерции всей
системы J1 будет равен сумме моментов инерции самой платформы J0 и лежащего на ней тела
– Jx0. Чтобы определить момент инерции исследуемого тела, нужно из полученного значения J вычесть значение J0.
Jx0 = J1 − J0. |
(11.20) |
3)Для проверки теоремы о переносе осей моментов инерции берут два совершенно одинаковых груза массы m, которые устанавливают на на расстоянии A по обе стороны от центра платфор-
мы. По формуле (11.17) определяют момент инерции платформы с двумя грузами J2, затем, вычтя из него момент инерции пустой платформы J0, получают момент инерции системы двух грузов JxA относительно оси, проходящей через центр платформы.
4)Проверяют теорему Гюйгенса-Штейнера, сравнивая вычисленное значение момента инерции
JxA теор = 2(Jx0 + mA2) |
(11.21) |
с экспериментальным результатом, полученным в предыдущем пункте.
5)Повторяют опыт для другого расстояния A по двум предыдущим пунктам.
6)Сравните экспериментальные значения J0 и JxA с теоретическими значениями для тел пра-
вильной геометрической формы, найденными по соответствующим формулам (прил. А).
11.4. Контрольные вопросы |
6 |
|
|
11.4. Контрольные вопросы
1)Что называют моментом силы? Что называют моментом инерции материальной точки? тела?
2)Каков физический смысл момента инерции тела?
3)Чему равна кинетическая энергия вращающегося тела?
4)Как теоретически можно вычислить момент инерции тела любой формы относительно оси вращения? Вывести момент инерции тела правильной геометрической формы (шар, диск, стержень).
5)Сформулируйте теорему о переносе осей момент инерции? Каково её практическое значение?
6)Какова общая идея метода определения моментов инерции тел при помощи крутильных колебаний? Какое свойство момента инерции при этом используется?
7)Какой закон положен в основу вывода основной расчётной формулы (11.17)?
8)При каких упрощающих предложениях выведена формула (11.17)?
9)Выполняется ли в ваших опытах условие (11.18)? Сделайте соответствующие расчеты.

Приложение А.
Моменты инерции тел правильной геометрической формы
Таблица А.1. Моменты инерции тел правильной геометрической формы
|
№ п.п. |
Тело |
Положение оси |
Формула |
||||
|
|
|
|
|
|
|
|
|
|
1 |
Полый тонкостенный |
Ось |
|
|
|
|
|
|
|
цилиндр или кольцо, |
цилиндра |
|
mr2 |
|||
|
|
радиус r, |
|
|
|
|
|
|
|
|
масса m |
|
|
|
|
|
|
|
2 |
Сплошной цилиндр |
Ось |
|
|
|
|
|
|
|
или диск |
цилиндра |
|
21 mr2 |
|||
|
|
радиус r, |
|
|
|
|
|
|
|
|
масса m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
Полый толстостенный |
Ось |
|
|
|
|
|
|
|
цилиндр |
цилиндра |
m |
R2 |
− m |
r2 |
|
|
|
2 |
2 |
|||||
|
|
внешний радиус R, |
|
|
|
|
|
|
|
|
внутренний радиус r, |
|
|
|
|
|
|
|
|
масса m |
|
|
|
|
|
|
|
4 |
Сплошной цилиндр |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
|
|
радиус r, |
цилиндру |
mr4 |
+ ml12 |
|||
|
|
длина l, |
и проходит через |
|
|
|
|
|
|
|
масса m |
его центр масс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Полый тонкостенный цилиндр |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
|
|
радиус r, |
цилиндру |
mr2 |
+ ml12 |
|||
|
|
длина l, |
и проходит через |
|
|
|
|
|
|
|
масса m |
его центр масс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7

8
Таблица А.2. Моменты инерции тел правильной геометрической формы (продолжение)
|
№ п.п. |
Тело |
Положение оси |
|
Формула |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
Прямой тонкий |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
|
стержень |
стержню |
|
|
|
|
1 |
|
|
ml2 |
|
|
|
|
|
|
12 |
|||||
|
|
длина l, |
и проходит через |
|
|
|
|
|
|
|
|
|
|
масса m |
его центр масс |
|
|
|
|
|
|
|
|
|
7 |
Прямой тонкий |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
|
стержень |
стержню |
|
|
|
|
31 ml2 |
|||
|
|
длина l, |
и проходит через |
|
|
|
|
|
|
|
|
|
|
масса m |
его конец |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
Тонкая прямоугольная |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
|
пластина |
пластине |
|
1 |
m(a2 + b2) |
|||||
|
|
|
12 |
||||||||
|
|
длина a, |
и проходит через |
|
|
|
|
|
|
|
|
|
|
ширина b |
её центр масс |
|
|
|
|
|
|
|
|
|
9 |
Тонкостенная сфера |
Проходит |
|
|
|
|
|
|
|
|
|
|
радиус r, |
через |
|
|
|
|
32 mr2 |
|||
|
|
масса m |
центр сферы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
Сплошной |
Проходит |
|
|
|
|
|
|
|
|
|
|
шар |
через |
|
|
|
|
52 mr2 |
|||
|
|
радиус r, |
центр шара |
|
|
|
|
|
|
|
|
|
|
масса m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
Сплошной |
Ось |
|
|
|
|
|
|
|
|
|
|
конус |
конуса |
|
|
|
3 |
|
mr2 |
||
|
|
|
|
|
10 |
||||||
|
|
радиус r, |
|
|
|
|
|
|
|
|
|
|
|
масса m |
|
|
|
|
|
|
|
|
|
|
12 |
Квадрат |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
|
сторона a, |
плоскости квадрата |
|
|
|
|
61 ma2 |
|||
|
|
масса m |
и проходит через |
|
|
|
|
|
|
|
|
|
|
|
его центр масс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
Правильный |
Перпендикулярна |
|
|
|
|
|
|
|
|
|
|
треугольник |
плоскости треугольника |
|
|
|
1 |
ma2 |
|||
|
|
|
|
12 |
|||||||
|
|
сторона a, |
и проходит через |
|
|
|
|
|
|
|
|
|
|
масса m |
его конец |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Литература
1.Майсова, Н. Н. Практикум по курсу общей физики / Н. Н. Майсова. – М.: Высшая школа, 1970.
2.Иверонова, В. И. Физический практикум: Механика и молекулярная физика / В. И. Иверонова.
– М.: Наука, 1967.
3.Комплект описаний к “Типовому комплекту учебного оборудования ”Механика“ на 6 рабочих мест” / НПИ “Учебная техника и технологии” ЮУрГУ – Челябинск, 2008.
4.Каленков, С. Г. Практикум по физике. Механика / С. Г. Каленков. – М.: Высшая школа, 1990.
5.Сивухин, Д. В. Общий курс физики. Т.1: Механика / Д. В. Сивухин. – М.: Наука, 1989 (и др. года издания).
6.Савельев, И. В. Курс общей физики (Том 1. Механика) / И. В. Савельев. – М.: Наука, 1970 (и др. года издания).
7.Хайкин, С. Э. Физические основы механики / С. Э. Хайкин. – М.: Наука, 1971
8.Касандрова, О. Н. Обработка результатов наблюдений / О. Н. Касандрова, В. В. Лебедев. – М.: Наука, 1970.
9.Зайдель, А. Н. Элементарные оценки ошибок измерений / А. Н. Зайдель. – М.: Наука, 1967.
10.Щиголев, Б. Н. Математическая обработка наблюдений / Б. Н. Щиголев. – М.: Физматгиз, 1962.
9
