
Mechanics-18
.pdfМинистерство образования и науки Российской Федерации Ярославский государственный университет
им. П. Г. Демидова
В.П. Алексеев, Е. О. Неменко,
В.А. Папорков, Е. В. Рыбникова
Лабораторная работа № 18
Определение ускорения свободного падения
из колебаний математического и физического маятников.
Ярославль 2013

Лабораторная работа № 18.
Определение ускорения свободного падения из колебаний математического и физического маятников1
Цель работы:
•изучение законов колебательных движений на примере математического и физического маятников;
•определение ускорения свободного падения.
Оборудование:
•лабораторная установка “Математический и физический маятник”;
•линейка,
•штангенциркуль.
18.1. Краткая теория
18.1.1. Гармонические колебания
Гармоническими колебаниями физической величины x называется процесс изменения её во времени t по закону:
x = A sin |
T t + ϕ , |
(18.1) |
|
|
|
2π |
|
где A – амплитуда колебания, T – период колебания.
Величина 2Tπ t + ϕ носит название фазы, ϕ – начальной фазы. График такого колебания пред-
ставлен на рис. 18.1.
Из определения гармонического колебания следует, что период колебания является наименьшим промежутком времени, по истечении которого движение в точности повторяется. Действительно,
x = A sin |
T |
t + ϕ = A sin |
T (t + T ) + ϕ . |
||
|
|
2π |
|
|
2π |
За время t = T совершается одно полное колебание. Амплитуда колебания A равна максимальному значению x. Величина ϕ соответствует фазе в начальный момент времени (t = 0) и называется
начальной фазой.
1Ранее данная работа имела номер 10.
1

18.1. Краткая теория |
2 |
|
|
|
|
Рис. 18.1. Гармонические колебания |
|
|
Величина |
2π |
= ω называется круговой (циклической) частотой. Если начальная фаза равна |
||
T |
||||
|
|
|
||
ϕ = π/2, то уравнение гармонического колебания записывается в виде: |
|
|||
|
|
x = A cos(ωt). |
(18.2) |
|
18.1.2. Математический маятник
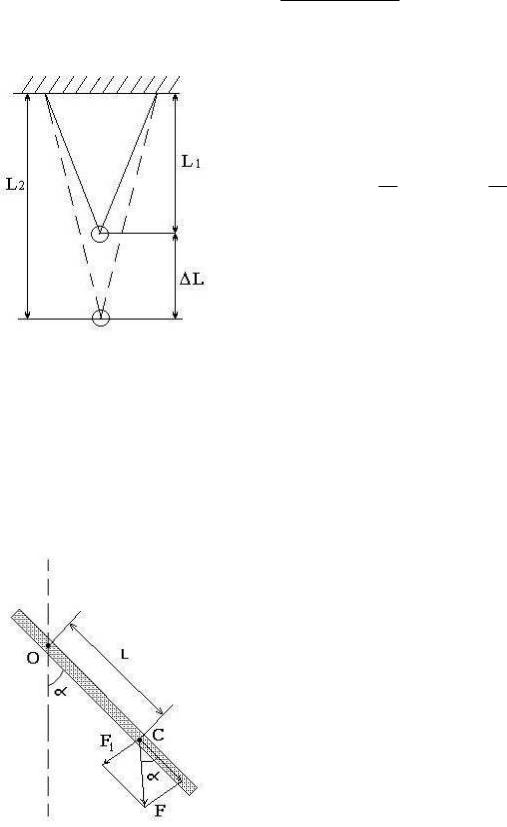
Математическим маятником называется колебательная система, состоящая из материальной точки, прикреплённой к концу идеально гибкой, нерастяжимой и невесомой нити, второй конец которой закреплён неподвижно в точке подвеса. Исследуемый в лабораторной установке маятник схематически изображён на рис. 18.2. Он представляет собой стальной шарик радиусом r с ушком
на бифилярном подвесе. Тонкая нить пропущена через ушко шарика, концы нити закреплены на стойке. Длина подвеса L может регулироваться в пределах от нескольких сантиметров до 0.5 м.
Момент инерции маятника складывается из момента инерции шарика и момента инерции нити подвеса относительно оси OO′. Пренебрегая моментом инерции нити, запишем момент инерции маятника относительно оси OO′
в виде:
J0 = Jc + mL |
2 |
= |
2 |
|
2 |
2 |
|
(18.3) |
|
|
mr |
|
+ mL |
. |
|||
|
5 |
|
Рис. 18.2. Математический маятник
Jсист
J
Соотношение (18.3) следует из теоремы ГюйгенсаШтейнера, поскольку момент инерции однородного шара радиусом r и массой m относительно оси, проходящей через его центр, равен Jc = 25 mr2.
Рассмотрим случай, когда радиус шарика мал по сравнению с длиной подвеса: r L. Тогда в (18.3) можно пренебречь слагаемым 2/5mr2, малым по сравнению с mL2,
и положить:
|
|
|
|
|
|
|
|
J0 = mL2. |
(18.4) |
|
В этом приближении J определяется, очевидно, с |
||||||||
небольшой систематической погрешностью: |
|
||||||||
|
|
2mr2 |
2 |
|
r |
2 |
|
||
= |
|
|
= |
|
|
|
|
, |
(18.5) |
5mL2 |
5 |
L |
|||||||
которую в условиях опыта легко оценить. С учётом (18.4) период колебаний маятника можно записать в виде:
T = 2πs |
|
g |
, |
(18.6) |
|
|
L |
|
|
18.1. Краткая теория |
3 |
|
|
где g – ускорение свободного падения.
Из формулы (18.6) следует, что период колебаний математического маятника не зависит от его массы m. Заметим, что формула (18.6) справедлива лишь для малых углов. Более точная формула
v
u
u
для определения периода имеет вид T = 2πt
g |
1 + 4 sin |
|
2 |
!. |
L |
1 |
2 |
α |
|
Длиной маятника является расстояние от центра тяжести до оси подвеса. Центр тяжести лабораторного маятника может не совпадать с геометрическим центром тяжести шарика, поэтому непосредственное измерение длины представляется некорректным. При определении ускорения свободного падения рассматривают колебания маятника для двух различных его длин. Согласно формуле (18.6), периоды колебаний двух маятников с различными длинами равны
L1 |
|
|
|
L2 |
|
|||
T1 = 2πs |
|
|
, |
T2 = 2πs |
|
. |
(18.7) |
|
g |
g |
|||||||
Откуда определяем |
|
|
|
|
|
|
||
g = |
4π2(L1 − L2) |
|
(18.8) |
|||||
|
T12 |
− T22 |
||||||
|
|
|
|
|||||
Таким образом, для того, чтобы определить ускорение свободного падения, достаточно знать разницу длин математических маятников L и их периоды колебаний. При этом изме-
Рис. 18.3. К определение g с поморять длину можно по верхней, нижней, или любой другой удоб-
щью двух маятников разных длин ной точке шарика, главное чтобы эта точка оставалась неизменной во всех опытах.
18.1.3. Физический маятник
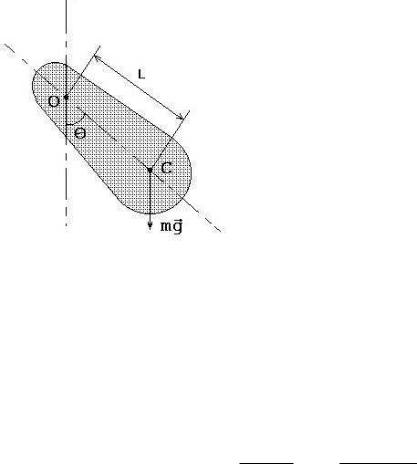
Физическим маятником называется тело, укреплённое на неподвижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относительно этой оси (рис. 18.4). Покажем, что маятник, отклонённый на малый угол α от положения равновесия, будет
совершать гармонические колебания и найдем период колебаний такого маятника. Обозначим через J момент инерции маятника относительно оси O. Пусть точка C является центром тяжести.
На основании второго закона Ньютона для вращательного движения (М = Jε) имеем:
Jε = −F1L, |
(18.9) |
||||
где: |
|
|
|
||
F1 = F sin α |
(18.10) |
||||
d2 |
α |
. |
(18.11) |
||
ε = |
|
|
|||
dt2 |
|||||
|
|
|
|||
L = CO – расстояние от точки подвеса до центра тяжести. Знак минус выбран потому, что момент силы M стремится
вернуть маятник в положение равновесия, т. е. уменьшить угол α. Т. к. угол α мал, то sinα ≈ α и
|
|
|
F1 = mgα. |
(18.12) |
|
|
Подставляя (18.11) и (18.12) в уравнение (18.9) получим: |
||||
|
d2 |
α |
+ mgLα = 0. |
(18.13) |
|
|
J |
|
|
||
|
dt2 |
||||
|
|
|
|
||
Рис. 18.4. Физический маятник |
Частным решением последнего дифференциального урав- |
||||
|
нения является |
|
|
|
|
|
α = A cos ωt, |
|
|
(18.14) |
|
18.1. Краткая теория |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = r |
|
|
J , |
|
|
|
(18.15) |
|||
|
|
|
|
|
|
mgL |
|
|
|
|
||||
A – амплитуда колебаний маятника. |
|
|
|
|
|
|
|
|
|
|
|
|||
Дважды дифференцируя (18.14), получим |
|
|
|
|
|
|
|
|
||||||
|
d2α |
|
2 |
|
|
|
mgL |
|
α |
(18.16) |
||||
|
|
= −Aω |
|
cos(ωt) = −A |
|
|
|
|
cos(ωt) = −mgL |
|
, |
|||
|
dt2 |
|
J |
|
||||||||||
|
|
|
|
|
|
2 |
|
|
||||||
Подставляя (18.14) и (18.16) в (18.13), можно убедиться, что левая часть уравнения тождественно равна нулю.
Сравнивая (18.15) и (18.1), получим |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = 2πs |
|
|
J |
|
, |
(18.17) |
|||
|
|
|
|
|
|
||||||
mgL |
|||||||||||
или |
|
|
|
|
|
||||||
|
|
T = 2πs |
Lпр |
, |
(18.18) |
||||||
|
|
|
|
||||||||
g |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
J = J0 + mL2, |
(18.19) |
где J0 – момент инерции маятника относительно оси, параллельной оси качания и проходящей через центр масс C маятника, L – расстояние между точками O и C.
Подставляя (18.19) в (18.17), получаем
ss
T = 2π mgl |
+ g = 2π |
g |
mL + L , |
(18.20) |
|||
|
J0 |
|
L |
1 |
|
J0 |
|
18.1. Краткая теория |
5 |
|
|
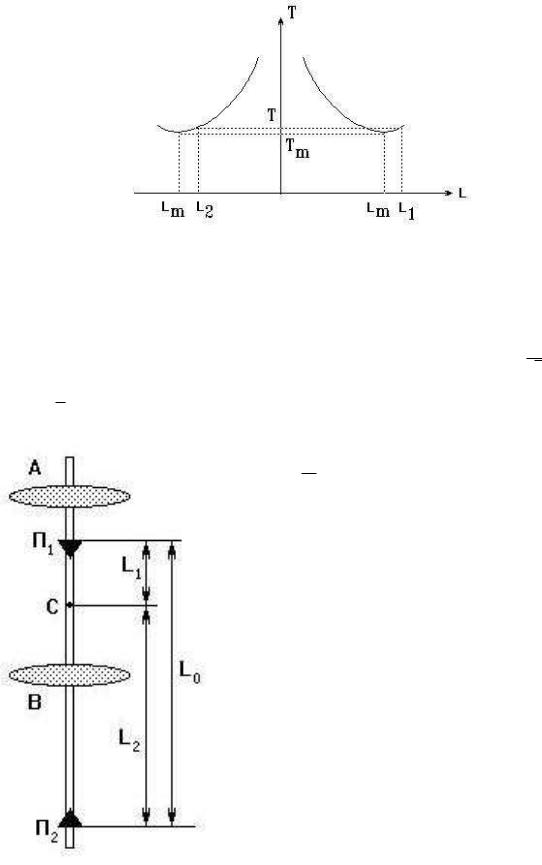
Рис. 18.6. Зависимость T (L)
Обсудим качественно характер зависимости периода колебаний от расстояния до оси качания. При очень малых L момент силы тяжести M = −mgL sin θ (рис. 18.5), стремящийся вернуть маят-
ник в положение равновесия, становится очень малым и период колебаний резко возрастает. В пределе L → 0 момент силы тяжести равен нулю и колебания вообще невозможны, маятник находится
в положении равновесия. Это согласуется с формулой (18.20): при L → 0 период T ≈ 1 → ∞.
√
L
В обратном пределе очень больших L можно пренебречь J0 по сравнению с mL2 и рассматривать физический маятник как математический с длиной подвеса L. В этом случае период колебаний
q
T = 2π |
L . |
|
g |
При возрастании L период T сначала убывает до некоторого минимального значения Tm = Tmin, а затем снова неограниченно возрастает при L → 0 (см. (18.20)). Период минимален
q
при Lm = |
J0 |
. |
|
||
|
m |
|
Качественно вид зависимости T (L) изображён на рис. 18.6. Значению L = 0 соответствует центр масс маятника. Если под-
вешивать маятник по другую сторону от центра масс, то зависимость T (L) будет точно такой же. Поэтому график T (L)
имеет две симметричные ветви, соответствующие положению точки подвеса маятника слева и справа от его центра масс. По каждую сторону от центра масс маятника имеется по два положения опорных призм, при которых периоды колебаний маятника совпадают.
Но в случае, когда T = Tmin таких точек по одной от центра масс, причем L1 = L2.
В данной установке оборотный маятник представляет собой стальной стержень, на котором находятся два подвижных груза A и B (рис. 18.7). Две легкие опорные призмы П1 и П2 мо-
гут перемещаться по стержню и фиксироваться винтами в разных его точках. Маятник совершает колебания в вертикальной плоскости. Перемещая по стержню грузы, можно изменять период колебаний маятника.
Попробуем найти такие два положения L1 и L2 опорных
призм по разные стороны от центра масс, чтобы периоды колебаний маятника совпадали: Т(L1) = Т(L2.
Рис. 18.7. Устойство лабораторного оборотного маятника

18.2. Описание экспериментальной установки |
6 |
|
|
Как видно из ((18.20), для этого необходимо выполнение равенства:
T = T (L1) = T (L2) =
= 2πs |
g J0 mL1 + l1 |
= |
|||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 2πs |
L |
|
g |
|
, |
|
||||||
|
|
|
|
|
|
|
1 + L2 |
|
|
|
|||
|
J0 |
+ L1 = |
|
J0 |
+ L2, |
||||||||
|
|
|
|
|
|||||||||
mL1 |
|
mL2 |
|
|
|
||||||||
L1 = L2
1
L2 = J0 mL1 .
Следовательно, ускорение свободного падения может быть определено по формуле
4π2
g = T 2 (L1 + L2).
(18.21)
(18.22)
(18.23)
Как видно из (18.23), для нахождения g достаточно измерить только две величины: расстояние L0 = L1 + L2 между рёбрами опорных призм и период колебаний маятника T в положении L1 и в “перевёрнутом” положении L2, таком, чтобы T = T1 = T2.
18.2. Описание экспериментальной установки
Общий вид универсального маятника FPM-04 представлен на рис.18.8. Основой установки является колонка 1, наверху которой смонтирован поворотный кронштейн 2. Также на колонку надет и нижний кронштейн с фотоэлектрическим датчиком 3, который может перемещаться вдоль неё и фиксироваться в произвольно выбранном положении.
С одной стороны кронштейна 2 находится математический маятник 4, с другой на вмонтированных вкладышах оборотный маятник 5. Длину математического маятника можно регулировать при помощи воротка, а ее величину определить по шкале на колонке. Оборотный маятник выполнен в виде стального стержня 5, на котором зафиксированы две повернутых навстречу друг к другy лезвиями призмы 7 и два груза 8. На стержне через каждые 10 мм выполнены кольцевые проточки, служащие для точного определения положения призм и грузов. Призмы и грузы можно можно перемещать вдоль стержня и фиксировать в любом положении. В основании имеются регулируемые ножки 10, которые позволяют произвести выравнивание прибора.
Фотоэлектрический датчик соединён с привинченным к основанию счётчиком-секундомером FPM-14 9. Описание и правила пользования им приведены в приложении А.1.
Также данная работа может выполняться на установке “Маятник универсальный ФМ-13”. Устройство и принцип работы установки ФМ-13 полностью аналогичны установке FPM-04. В комплект установки входит электронный счётчик-секундомер ФМ-1/1, описание и правила пользования которым приведены в приложении А.2.
18.3. Порядок выполнения работы
18.3.1.Исследование зависимости периода математического маятника от угла отклонения
1)Разверните верхний кронштейн установки математическим маятником вперёд. Установите датчик в самое нижнее положение. Установите длину математического маятника таким образом, чтобы риска на шарике совпадала с риской на датчике и добейтесь, чтобы шарик в состоянии покоя висел строго симметрично относительно датчика. Измерьте диаметр шарика и ширину датчика.

18.3. Порядок выполнения работы |
7 |
|
|
Рис. 18.8. Лабораторная установка “Маятник универсальный FPM-04”
2)Отклоните шарик таким образом, чтобы он только-только выходил за пределы датчика. Измерьте время десяти колебаний и вычислите период оного колебания. Правила проведения измерений с применением электронного счётчика-секундомера описаны в приложении А. Определите угол отклонения маятника по формуле
s + d
α = arctg 2 2 , L
где s – ширина датчика, d – диаметр шарика, L – длина маятника до центра шарика. Повторите
опыт три раза.
3)Отклоните шарик таким образом, чтобы расстояние x между ним и датчиком составляло 1 см. Измерьте время десяти колебаний и вычислите период оного колебания. Определите
угол отклонения маятника по формуле
s + d + x
α = arctg 2 2 , L
где s – ширина датчика, d – диаметр шарика, L – длина маятника до центра шарика. Повторите
опыт три раза.
4)Аналогично произведите измерения для x = 2, 3, . . . , 10 см.
5)Постройте график зависимости периода от угла отклонения T = T (α). Определите, при каком
максимальном угле отклонения, колебания сохраняют гармонический характер.
18.3.2. Измерение G с помощью математического маятника
1)Разверните верхнюю часть установки математическим маятником вперёд. Установите датчик в самое нижнее положение. Установите длину математического маятника таким образом, чтобы шарик риска на шарике совпадала с риской на датчике.
18.4. Контрольные вопросы |
8 |
|
|
2)Отклоните маятник на (4 − 5)◦ от положения равновесия. Измерьте время 10 колебаний и вычислите период одного колебания T1. Период определяется не менее 5 раз и вычисляется
ошибка измерений.
3)Поднимите шарик на (15−20) см, укорачивая нить, и переместить датчик на соответствующую
высоту (риски на шарике и датчике также должны совпасть). Определить период колебаний маятника T2 аналогично предыдущему пункту.
4)Определите ускорение свободного падения g по формуле (18.8)
18.3.3. Измерение G с помощью физического маятника
1)Поверните верхний кронштейн физическим маятником вперёд. Зафиксируйте грузы на стержне несимметрично, т. о., чтобы один из них находился вблизи конца стержня, а другой вблизи его середины, как изображено на рис. 18.7. Опорные призмы маятника закрепите по обеим сторонам стержня на одинаковом расстоянии от его концов, которое должно составлять 10 − 15 см, таким образом, чтобы они были обращены друг к другу вершинами.
2)Перемещая грузы, добейтесь того чтобы получился оборотный маятник, т. е. чтобы периоды колебаний на обеих призмах T1 и T2 были равны.
3)Измерьте время 10 колебаний маятника и определить период одного колебания.
4)По формуле (18.23) найти величину g.
18.4. Контрольные вопросы
1)Какому методу измерений ускорения силы тяжести вы отдаёте предпочтение? Почему?
2)Как влияют на точность опытов колебания температуры, сила трения, амплитуда колебаний маятника?
3)Что называется приведенной длиной физического маятника?
4)При каком условии точка подвеса и центр качания физического маятника расположены симметрично относительно его центра масс?
5)При каком расстоянии от опорной призмы до центра масс период колебаний маятника минимален?
6)Покажите, что точка опоры маятника и точка его качания лежат по разные стороны от центра масс.
7)Выведите формулу для периода нелинейных колебаний математического маятника.
8)От чего зависит величина ускорения силы тяжести?
9)Рассмотрите оборотный маятник, имеющий вид тонкого однородного стержня длины L с дву-
мя невесомыми подвижными призмами. Как в этом случае будет зависеть величина g/g от
положения призм относительно центра тяжести маятника? Какое расположение призм кажется вам более разумным? Оцените значения t и t, соответствующие величине g/g = 5· 10−2,
а также время, необходимое для проведения эксперимента с заданной точностью.
10)Сформулируйте теорему Гюйгенса.
11)Где и для каких целей используются маятники?

Приложение А.
Правила пользования электронными секундомерами
А.1. Правила пользования счетчиком-секундомером FPM-14
На передней панели счётчика расположены кнопки “Сеть” 1, “Стоп” 2 и “Сброс” 3, а также два цифровых табло, отображающих прошедшее время 5 и количество периодов колебаний 4 соот-
ветственно. Запуск секундомера происходит после нажатия кнопки “Сброс”, в момент пересечении маятником датчика. Остановка отсчёта происходит при нажатии кнопки “Стоп” в конце следующего периода колебания, т. е., дя фиксации времени 10 колебаний, следует нажимать кнопку “Стоп”, когда на табло 4 высветится значение “9”.
Рис. А.1. Счётчик-секундомер FPM-14
А.2. Правила пользования счетчиком-секундомером ФМ-1/1
Правила пользования счетчиком-секундомером ФМ-1/1 аналогичны правилам пользования прибором FPM-14, за исключением того, что функции “Пуск” и “Сброс” разнесены по разным кнопкам (1 и 3 соответственно) и расположением выключателя питания на задней панели, в верхнем правом
углу.
Рис. А.2. Счётчик-секундомер ФМ-1/1
9
