К зачету по МО

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Н. Э. БАУМАНА

Национальный Исследовательский Университет техники и технологий

Практическая часть подготовки к зачету по:

“Методы оптимизации”

Вариант 8

Выполнил: Лапин А.И.

Группа: СМ10-81

Проверил: Аттетков А.В

Шишкина С.И.

Москва 2020

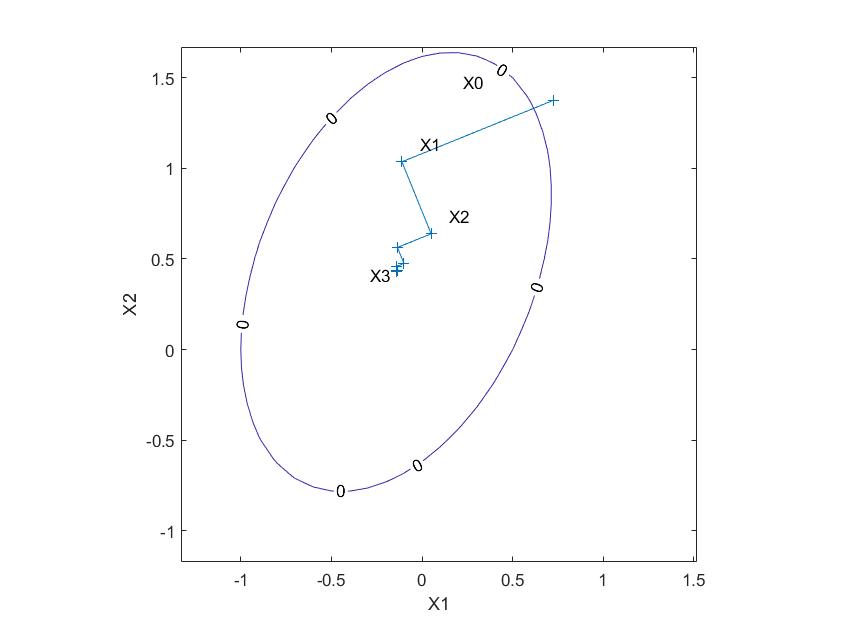
1. Привести квадратичную функцию к каноническому виду, указав

ортогональное преобразование. Построить линии уровня. Указать

минимальное значение функции и точку минимума.

2. Минимизировать функцию методами

• градиентным (с постоянным шагом, с дроблением шага, методом

наискорейшего спуска),

• сопряженных направлений (Флетчера-Ривса, Пауэлла, сопряженных

относительно матрицы вторых производных),

• используя методом Ньютона или его модификации.

Целевая функция:

Дано уравнение линии 2-ого порядка

Уравнение имеет вид:

,

где

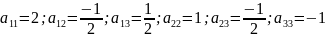
Инвариантами данного уравнения при преобразовании координат являются определители:

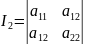
Подставляем коэффициенты

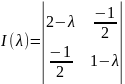
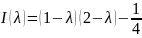
Т.к. , то по признаку типовых линий данное уравнение имеет тип: эллипс.

Составим характеристическое уравнение для линии:

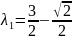
тогда канонический вид уравнения будет

приведено к каноническому виду

,

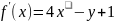
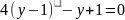
AC-B²>0 – имеет экстремум

A= ; B= C=

8-1>0 – имеет экстремум, А>0 – точка минимума в М₀

– минимальное значение

Минимизация функций

Квазиньютоновский

Точка (0; )

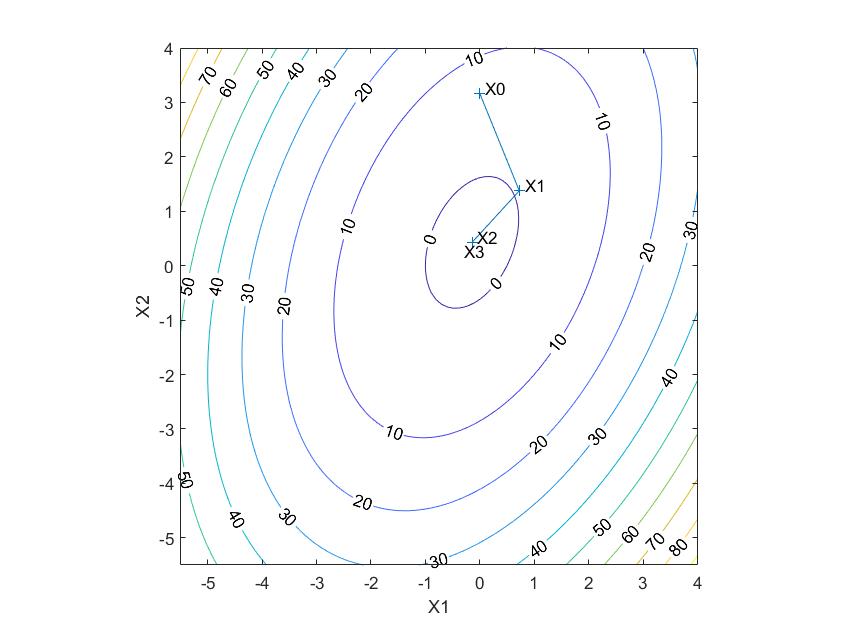
Наискорейшего спуска