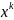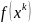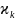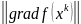ДЗ_МО Лапин
.docx

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Н. Э. БАУМАНА
Национальный Исследовательский Университет техники и технологий
Домашнее задание № 1 по дисциплине:
“Методы оптимизации”
Вариант 8

Выполнил: Лапин А.И.
Группа: СМ10-81
Проверил: Аттетков А.В
Шишкина С.И.
Москва 2020
Целевая функция:
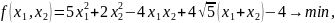
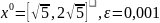 .
.
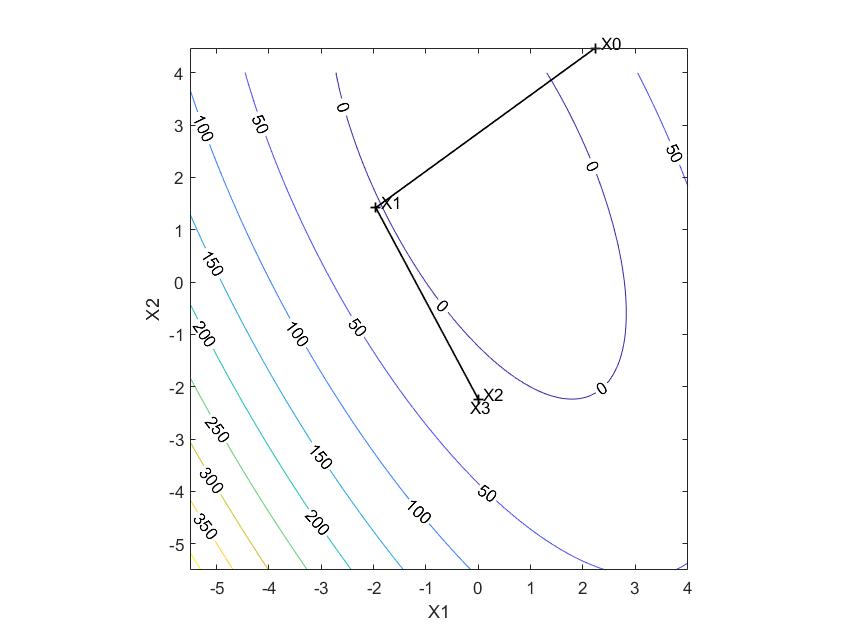
Метод наискорейшего спуска
Х2
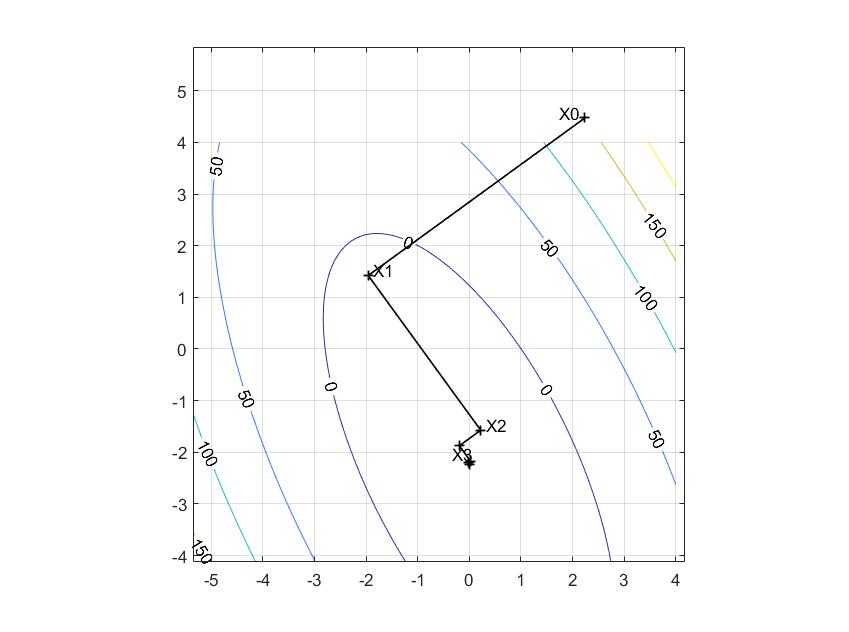
Х1
k |
|
|
|
|
0 |
(2.2361; 4.472) |
151.00 |
0 |
0 |
1 |
(-1.9578; 1.4220) |
-6.719 |
0.085 |
60.827 |
2 |
(0.2208; -1.5736) |
-22.294 |
0.441 |
8.409 |
3 |
(-0.1933; -1.8748) |
-23.832 |
0.085 |
6.006 |
4 |
(0.0218; -2.1707) |
-23.983 |
0.441 |
0.830 |
5 |
(-0.0191; -2.2004) |
-23.998 |
0.085 |
0.593 |
6 |
(0.0022; -2.2296) |
-23.999 |
0.441 |
0.082 |
7 |
(-0.0019; -2.2325) |
-24.000 |
0.085 |
0.058 |
8 |
(2.1263е-4; -2.2354) |
-24.000 |
0.441 |
0.008 |
Метод сопряженных градиентов
Х1
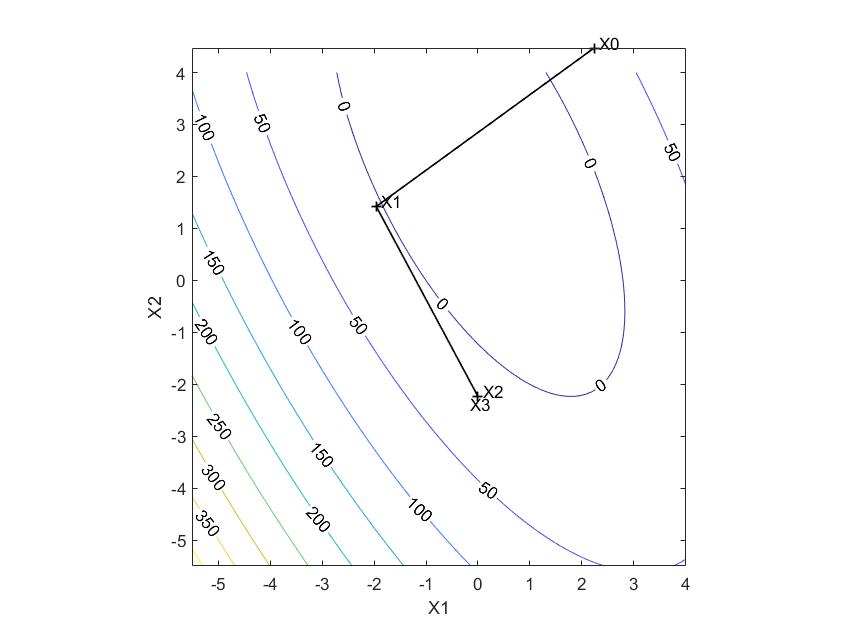
k |
|
|
|
|
0 |
(2.236; 4.472) |
151.00 |
0 |
0 |
1 |
(-1.9578; 1.422) |
-14.719 |
0.0853 |
60.8276 |
2 |
(5.1е-15; -2.2361) |
-24 |
0.4887 |
8.4093 |
3 |
(-5.2е-16; -2.2361) |
-24 |
0.0834 |
7.628e-14 |
Метод Дэвидона-Флетчера-Пауэлла
k |
|
|
|
|
0 |
(2.236; 4.472) |
151.00 |
0 |
0 |
1 |
(-1.958; 1.422) |
-6.719 |
0.0853 |
60.827 |
2 |
(-4.441е-16; -2.236) |
-24 |
0.4981 |
8.409 |
3 |
(-8.588е-17; -2.236) |
-24 |
0.0906 |
8.881e-15 |
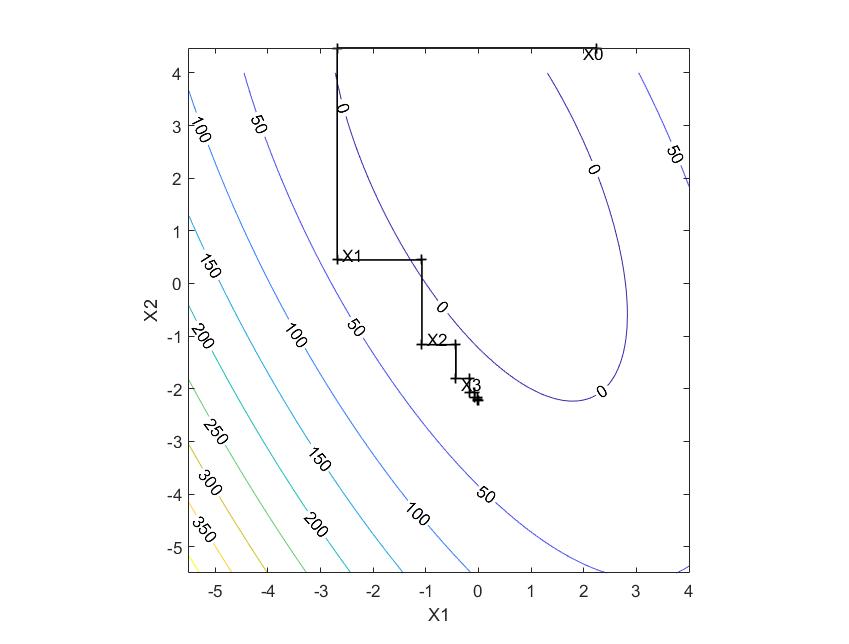
Циклический покоординатный спуск
k |
|
|
|
0 |
(2.236; 4.472) |
151.00 |
0 |
1 |
(-2.683; 0.447) |
-2.40 |
6.356 |
2 |
(-1.073; -1.162) |
-20.544 |
2.2768 |
3 |
(-0.429; -1.807) |
-23.447 |
0.9107 |
4 |
(-0.1717; -2.064) |
-23.911 |
0.3643 |
5 |
(-0.0687; -2.167) |
-23.9858 |
0.1457 |
6 |
(-0.0275; -2.2086) |
-23.9977 |
0.0583 |
7 |
(-0.011; -2.2251) |
-23.9996 |
0.0233 |
8 |
(-0.0044; -2.2317) |
-23.9999 |
0.0093 |
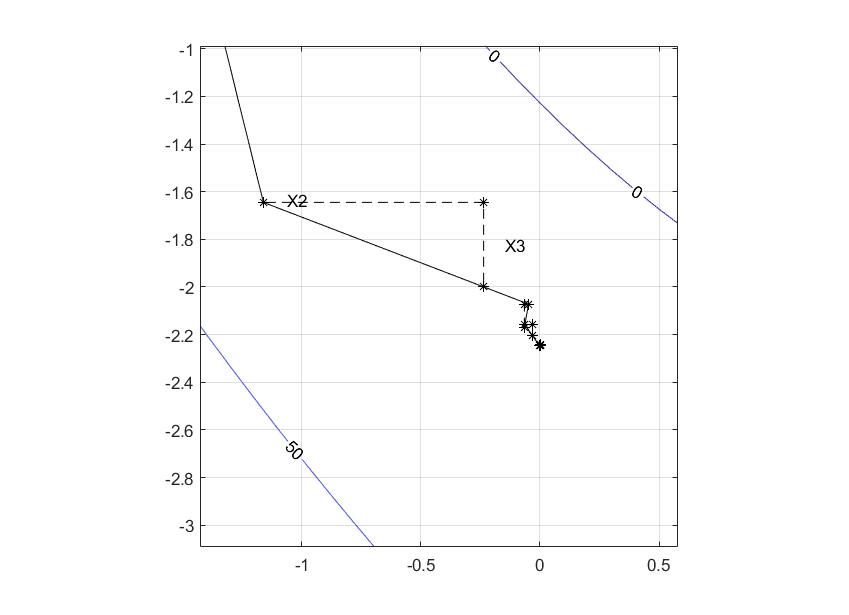
Метод Хука-Дживса


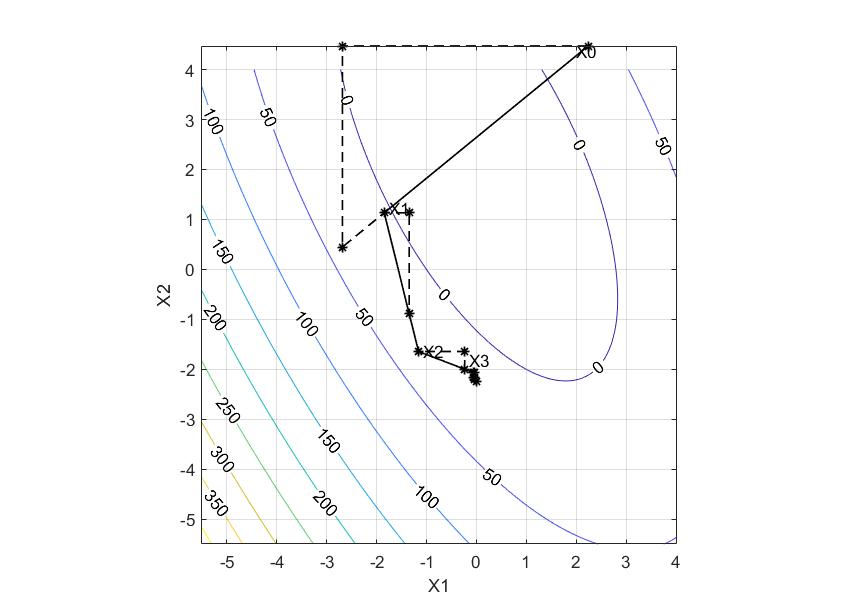
k |
|
|
|
|
0 |
(2.236; 4.472) |
151.00 |
0 |
0 |
1 |
(-1.8458; 1.1325) |
-9.1419 |
0.8298 |
5.274 |
2 |
(-1.1609; -1.6451) |
-19.3074 |
1.3743 |
2.8607 |
3 |
(-0.0478; -2.072) |
-23.9661 |
1.2040 |
1.1922 |
4 |
(-0.0634; -2.1581) |
-23.9875 |
0.8745 |
0.0875 |
5 |
(-0.0038; -2.2447) |
-23.9996 |
1.8521 |
0.1052 |
6 |
(0.0023; -2.2404) |
-24 |
0.8385 |
0.0075 |
Нерегулярный симплекс
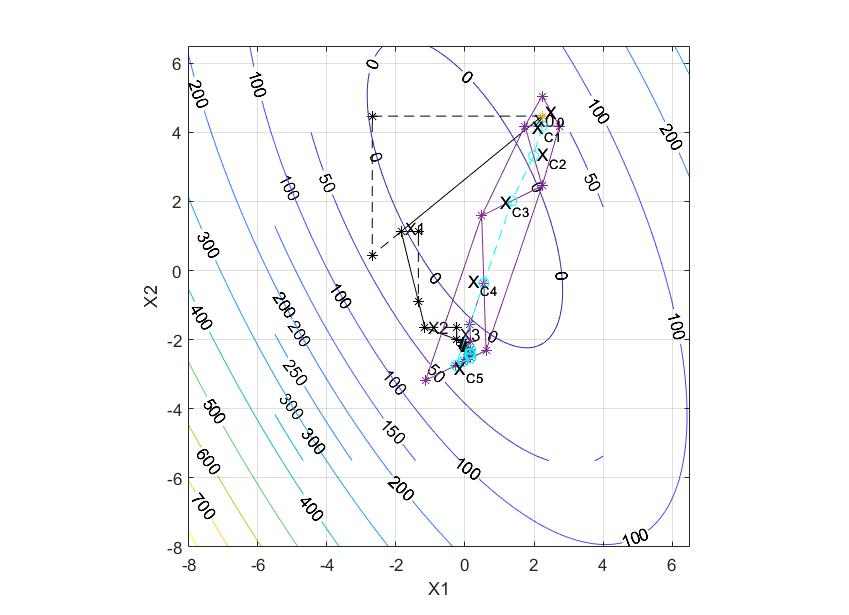
Коэффициент отражения: 𝛼=1
Коэффициент растяжения: 𝛽=2
Коэффициент сжатия: 𝛾=0.5
Начальная длина ребра: 𝑙=1
Количество итераций: 25
𝑥∗ = (0.1277; −2.3963)
𝑓(𝑥∗) = −23.9490