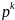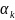7.3 Поиск при помощи регулярного симплекса ( )

k |
xk |
f(xk) |
lk |
|
||||
1 |
-4.47214 |
1 |
140.7771 |
2 |
50.40949 |
|||
2 |
-4.47214 |
-0.1547 |
96.53706 |
2 |
48.62259 |
|||
3 |
-3.47214 |
-0.73205 |
41.62389 |
2 |
31.27746 |
|||
4 |
-3.47214 |
-1.88675 |
14.00267 |
2 |
29.45836 |
|||
5 |
-2.47214 |
-2.4641 |
-13.6729 |
2 |
13.01268 |
|||
6 |
-2.47214 |
-3.6188 |
-24.6753 |
2 |
11.19465 |
|||
7 |
-2.47214 |
-4.19615 |
-27.1765 |
1 |
2.927951 |
|||
8 |
-1.97214 |
-4.48483 |
-27.5682 |
1 |
2.470212 |
|||
9 |
-2.22214 |
-4.62917 |
-27.9161 |
0.5 |
0.551766 |
|||
10 |
-2.22214 |
-4.48483 |
-27.9976 |
0.25 |
0.112814 |
|||
11 |
-2.22214 |
-4.41266 |
-27.9915 |
0.125 |
0.025697 |
|||
12 |
-2.22214 |
-4.48483 |
-27.9976 |
0.125 |
0.023767 |
|||
13 |
-2.25339 |
-4.46679 |
-27.9977 |
0.0625 |
0.01045 |
|||
14 |
-2.23776 |
-4.45776 |
-27.9993 |
0.03125 |
0.00257 |
|||
ε = 0,01
8 .
Поиск при помощи нерегулярного симплекса
(метод Нелдера-Мида)
.
Поиск при помощи нерегулярного симплекса
(метод Нелдера-Мида)
Параметры поиска:
– Длина ребра первого симплекса
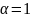 – Коэффициент
отражения
– Коэффициент
отражения
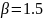 – Коэффициент
растяжения
– Коэффициент
растяжения
 – Коэффициент
сжатия
– Коэффициент
сжатия
– Коэффициент редукции

– Условие останова
ε = 0,01
 `
`
9. Метод проекций антиградиента

k |
xk |
|
|
|
|
||||||
0 |
-4.4721 |
1.0000 |
140.777 |
48.7214 |
0 |
0.0833 |
- |
||||
1 |
-2.2239 |
-0.2049 |
26.4209 |
16.9721 |
-25.5218 |
0.0867 |
2.5500 |
||||
2 |
-1.8211 |
-2.2121 |
-15.3947 |
-2.0701 |
-10.7162 |
0.2116 |
2.0472 |
||||
3 |
-2.7904 |
-3.8123 |
-23.387 |
2.6771 |
2.1314 |
0.1732 |
1.8709 |
||||
4 |
-2.3766 |
-3.4026 |
-23.8485 |
-1.0438 |
-1.2846 |
0.2237 |
0.5823 |
||||
5 |
-2.6274 |
-3.6715 |
-23.9051 |
1.0338 |
0.9673 |
0.1920 |
0.3677 |
||||
… |
… |
… |
… |
… |
… |
… |
… |
||||
15 |
-2.5161 |
-3.5611 |
-24.0195 |
0.0391 |
0.0411 |
0.2059 |
0.0159 |
||||
16 |
-2.5081 |
-3.5527 |
-24.0196 |
-0.0284 |
-0.0301 |
0.207 |
0.0117 |
||||
17 |
-2.5139 |
-3.5589 |
-24.0196 |
- |
- |
- |
0.0085 |
||||
ε = 0,01
1
 0.
Метод барьерных функций r
= 2.5 r
= 7
0.
Метод барьерных функций r
= 2.5 r
= 7
k |
xk |
f(xk) |
|
|
0 |
-4,47214 |
1 |
140,7771 |
- |
1 |
-3,77893 |
0,405594 |
87,7618 |
64,18018 |
2 |
-2,19484 |
-1,08435 |
5,882787 |
46,78996 |
3 |
-1,36845 |
-2,43936 |
-18,1416 |
21,77088 |
4 |
-1,83598 |
-3,86463 |
-26,9046 |
8,685747 |
5 |
-2,24495 |
-4,17341 |
-27,7212 |
3,093565 |
… |
… |
… |
… |
… |
11 |
-2,23632 |
-4,4696 |
-28 |
0,031785 |
12 |
-2,23525 |
-4,47092 |
-28 |
0,020938 |
13 |
-2,23612 |
-4,47163 |
-28 |
0,006377 |
14 |
-2,2359 |
-4,47189 |
-28 |
0,0042 |
15 |
-2,23608 |
-4,47203 |
-28 |
0,001278 |
16 |
-2,23603 |
-4,47209 |
-28 |
0,000842 |
ε = 0,001

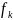 (xk)
(xk)