
Московский государственный технический
университет им. Н.Э. Баумана
Факультет «Фундаментальные науки»
Кафедра ФН-2 «Прикладная математика»
Домашнее задание по дисциплине
«Методы оптимизации»
Вариант 6
Студент: Новиков А.Д.
Группа: СМ9-81
Преподаватель: Аттетков А.В.
Москва, 2024 г.
1.Метод наискорейшего спуска
 ,
,
 ,
,

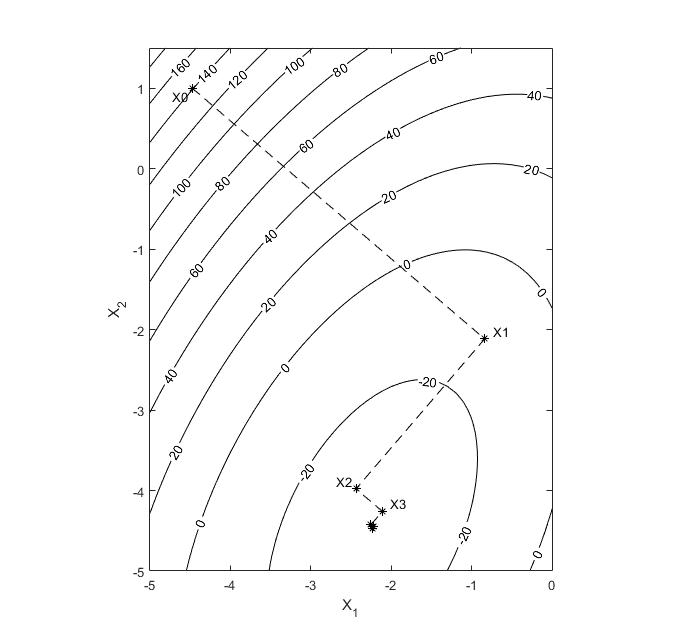
k |
xk |
f(xk) |
ϰk |
|
||||
0 |
-4.47214 |
1 |
140.7771 |
- |
- |
|||
1 |
-0.83916 |
-2.11516 |
-12.7959 |
0.074566 |
11.26838 |
|||
2 |
-2.4375 |
-3.97918 |
-26.6303 |
0.217907 |
5.78162 |
|||
3 |
-2.11023 |
-4.25981 |
-27.8766 |
0.074566 |
1.015103 |
|||
4 |
-2.25421 |
-4.42773 |
-27.9889 |
0.217907 |
0.520833 |
|||
5 |
-2.22473 |
-4.45301 |
-27.9990 |
0.074566 |
0.091445 |
|||
6 |
-2.2377 |
-4.46814 |
-27.9999 |
0.217907 |
0.046919 |
|||
7 |
-2.23505 |
-4.47041 |
-28.0000 |
0.074566 |
0.008238 |
|||
ε = 0,01
2. Метод градиентного спуска с дроблением шага
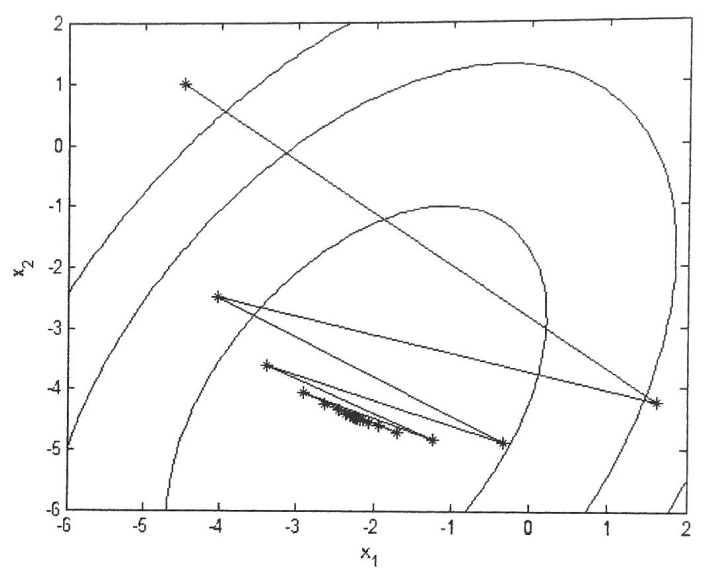
-
k
xk
f(xk)
ϰk
0
-4.4721
1.00000
140.7771
1.0000
64.1802
1
1.6180
-4.2221
57.4580
0.1250
47.3409
2
-4.0381
-2.4826
17.7004
0.1250
35.2377
3
-0.3403
-4.8758
-2.8860
0.1250
26.3384
4
-3.3858
-3.6251
-14.0215
0.1250
19.7238
5
-1.2377
-4.8352
-20.1741
0.1250
14.7828
6
-2.9168
-4.0637
-23.6072
0.1250
11.0838
7
-1.6915
-4.7104
-25.5314
0.1250
8.3117
8
-2.6275
-4.2594
-26.6120
0.1250
6.2334
9
-1.9340
-4.6147
-27.2194
0.1250
4.6749
10
-2.4584
-4.3567
-27.5609
0.1250
3.5062
11
-2.0672
-4.5544
-27.7530
0.1250
2.6296
…
…
…
…
…
…
29
-2.2351
-4.4726
-28.0000
0.1250
0.0148
30
-2.2368
-4.4718
-28.0000
0.1250
0.0111
31
-2.2355
-4.4724
-28.0000
0.1250
0.0083
ε = 0,01
3. Метод сопряженных направлений (Флэтчера-Ривса)
 ,
,
 ,
,
 ,
,
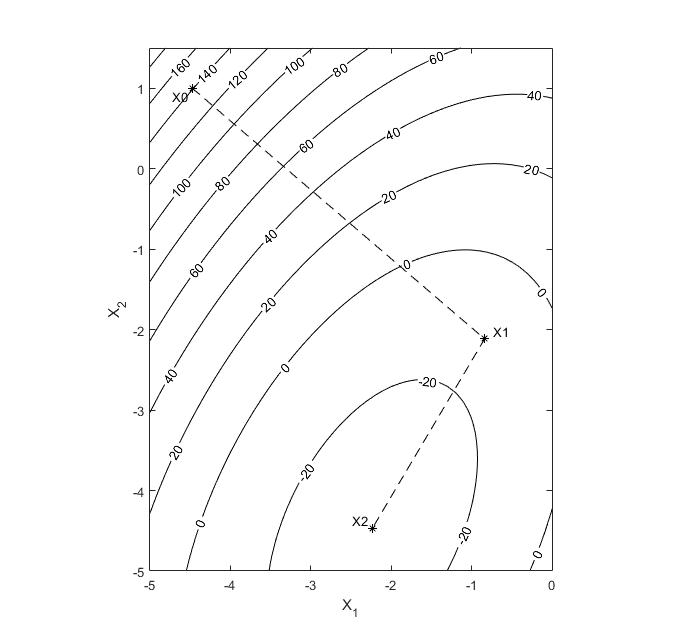
k |
xk |
f(xk) |
ϰk |
|
|
0 |
-4.47214 |
1.00000 |
140.7771 |
- |
64.18018 |
1 |
-0.83916 |
-2.11516 |
-12.7959 |
0.07456 |
11.26838 |
2 |
-2.23607 |
-4.47214 |
-28.0000 |
0.23948 |
0.00000 |
ε = 0,01
4. ДФП-метод
,
,
 ,
,
 ,
,
 ,
,
k |
xk |
f(xk) |
ϰk |
|
||||
0 |
-4.47214 |
1 |
140.7771 |
- |
64.18018 |
|||
1 |
-0.83916 |
-2.11516 |
-12.7959 |
0.074566 |
11.26838 |
|||
2 |
-2.23607 |
-4.47214 |
-28.0000 |
0.246862 |
0.00000 |
|||
ε = 0,01
5. Циклический покоординатный спуск
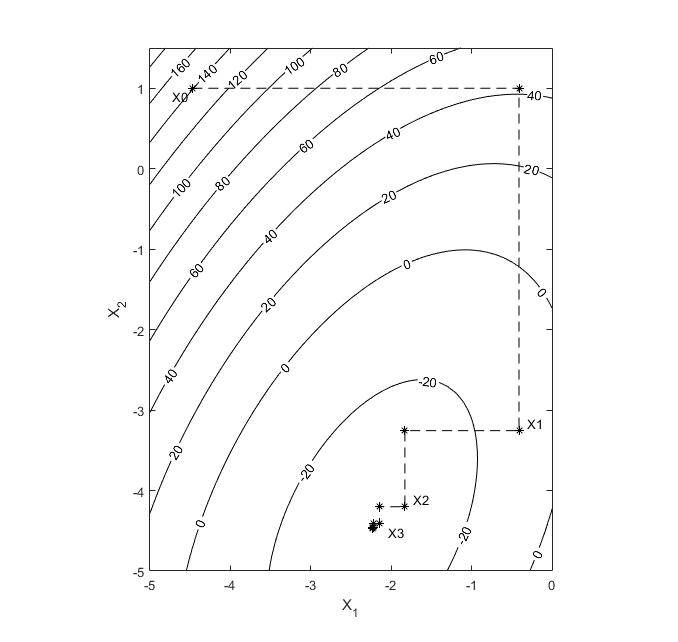
k |
xk |
f(xk) |
|
|||
0 |
-4.47214 |
1.00000 |
140.7771 |
- |
||
1 |
-0.41202 |
-3.25611 |
-12.4733 |
5.882088 |
||
2 |
-1.83072 |
-4.20191 |
-27.2333 |
1.705067 |
||
3 |
-2.14599 |
-4.41209 |
-27.9621 |
0.378904 |
||
4 |
-2.21605 |
-4.45879 |
-27.9981 |
0.084201 |
||
5 |
-2.23162 |
-4.46917 |
-27.9999 |
0.018711 |
||
6 |
-2.23508 |
-4.47148 |
-28.0000 |
0.004158 |
||
ε = 0,01


