Силовым полем называется часть пространства, в каждой точке пространства которого на материальную точку действует определенная сила, зависящая от координат точки
Стационарным силовым полем считается силовое поле, силы в котором не изменяются с течением времени
Потенциальнам силовым полем называется стационарное силовое поле, имеющее силовую функцию.
z 
F(x,y,z)
M
O |
y |
|
Силовая функция – U(x,y,z) функция, зависящая от |
||
координат точки, через которую проекции силы на |
||
координатные оси в каждой точке поля |
||
выражаются формулами: |
|
|
Fx U ; |
Fy U ; |
Fz U . |
x |
y |
z |
Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции
dA Fxdx Fydy Fzdz Ux dx Uy dy Uz dz dU ; dA dU
Полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках и не зависит от формы траектории, по которой происходит перемещение
M M
A dA dU U( x, y,z ) U( x0 , y0 ,z0 ) U U0 ;
M0 |
M0 |
A U U0 |
|
|
Потенциальное силовое поле – безвихревое
Вектор-градиент от скалярной функции U:
|
U |
|
|
U |
U |
. |
||||||
grad U i |
x |
j |
y |
k |
z |
|
||||||
|
|
|
|
|
|
|
|
|||||
Сила – градиент силовой функции: F grad U . |
|
|||||||||||
Если силовая функция существует, то: |
|
|
|
|
|
|
|
|||||
F |
2U |
|
|
Fy |
|
2U |
|
|
||||
x |
|
|
; |
|
|
|
|
|
|
|
. |
|
y x |
|
x |
x y |
|
||||||||
y |
|
|
|
|
|
|||||||
Потенциальное силовое поле – безвихревое
Так как |
2U |
|
|
|
2U |
|
|
, то |
||||||
y x |
|
x y |
|
|||||||||||
Аналогично |
Fz |
|
|
|
Fy |
0, |
||||||||
y |
|
|
z |
|||||||||||
Вектор вихря: F |
|
|
|
F |
y |
|
|
|||||||
rot F i |
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
z |
|
|
|
||||
|
|
y |
|
|
|
|
|
|
||||||
Fx Fy или Fx Fy 0.y x y x
Fx Fz 0.z x
|
|
|
F |
|
|
F |
|
|
|
j |
Fx |
z |
|
k |
y |
|
Fx |
; |
|
|
|
||||||||
|
|
z |
|
|
|
x |
|
|
|
|
|
x |
|
y |
|
||||
rot F 0
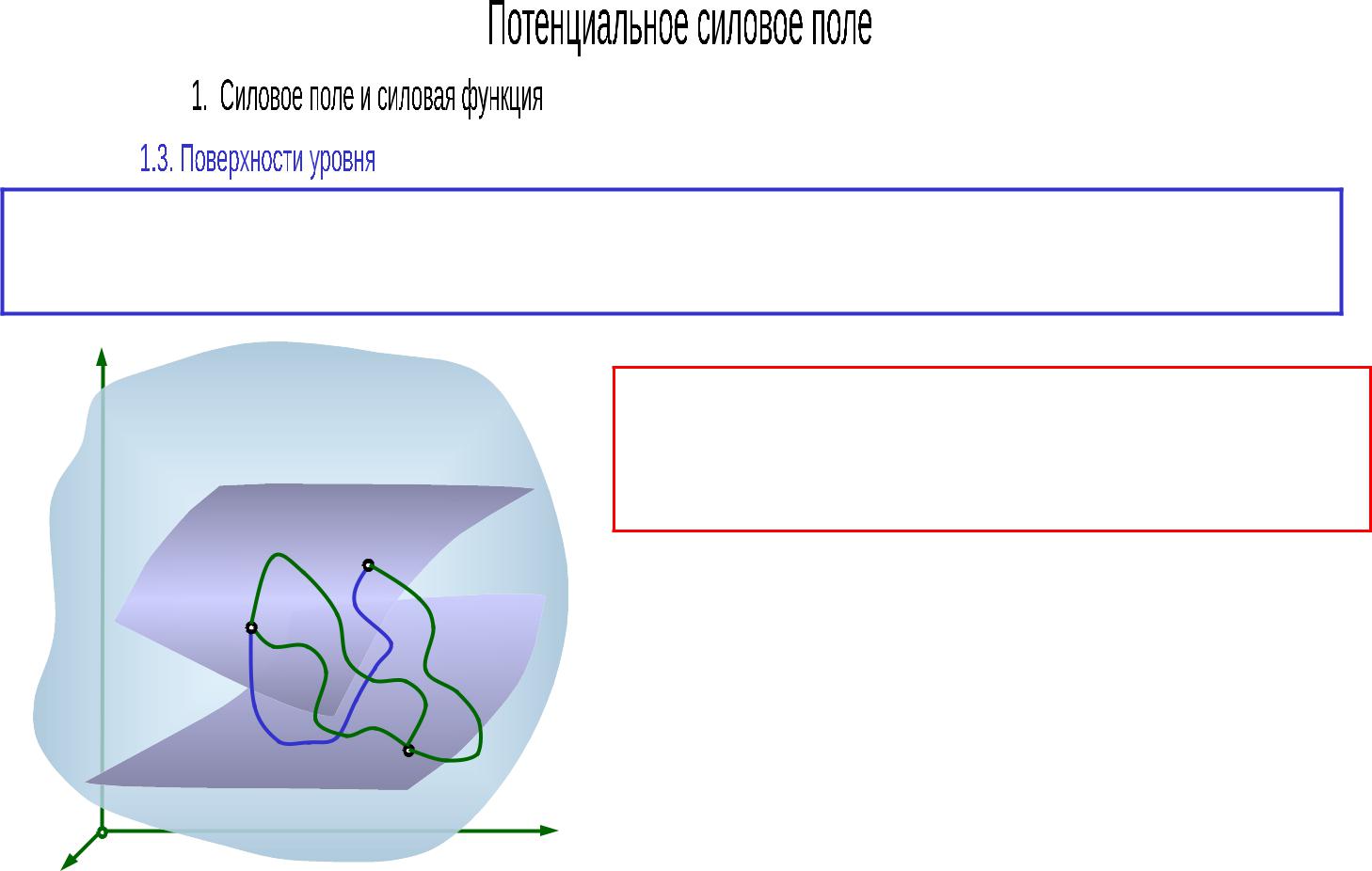
Точки потенциального силового поля, имеющие одинаковое значение силовой функции U=C, образуют поверхность, которую называют
поверхностью уровня
z
M2
U |
M |
|
A2 |
|
=C |
1 |
A3 |
||
|
|
|
||
|
|
|
A1 |
|
|
|
|
|
M0
U0=C0
Свойства поверхностей уровня:
1.Работа силы равна нулю, если начальная и конечная точки перемещения принадлежат одной поверхности уровня
A UM2 UM1 U U 0.
Работа силы при перемещении между двумя поверхностями уровня одинакова и не зависит от вида траектории и положения начальной и конечной точек на поверхностях уровня:
O |
y |
|
x
A1 A2 A3 U U0 .
Точки потенциального силового поля, имеющие одинаковое значение силовой функции U=C, образуют поверхность, которую называют
поверхностью уровня
z
U=C
O
F
900
900 |
M1 |
M
ds 
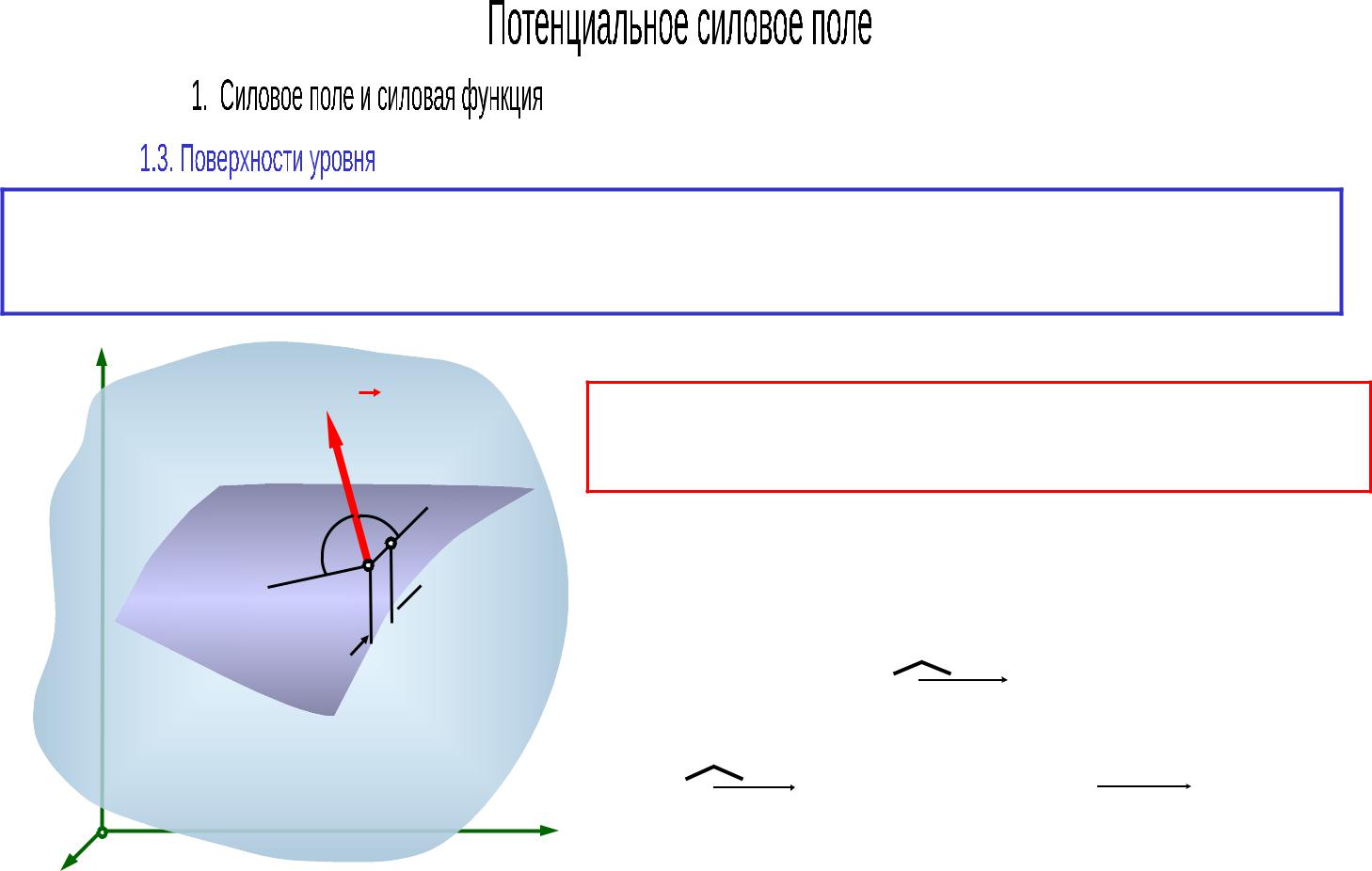
Свойства поверхностей уровня:
2.Сила в потенциальном силовом поле всегда перпендикулярна поверхности уровня.
Работа силы на перемещении ds между двумя бесконечно близкими точками M и
M1 на поверхности уровня:
|
dA Fdscos F , MM 1 |
UM1 UM 0; |
|||
y |
cos F , MM 1 |
0; |
|
F , MM 1 90 |
0 |
|
|
||||
x
Точки потенциального силового поля, имеющие одинаковое значение силовой функции U=C, образуют поверхность, которую называют
поверхностью уровня
z
U=C
O
x
F
ds
M1 900
900
M
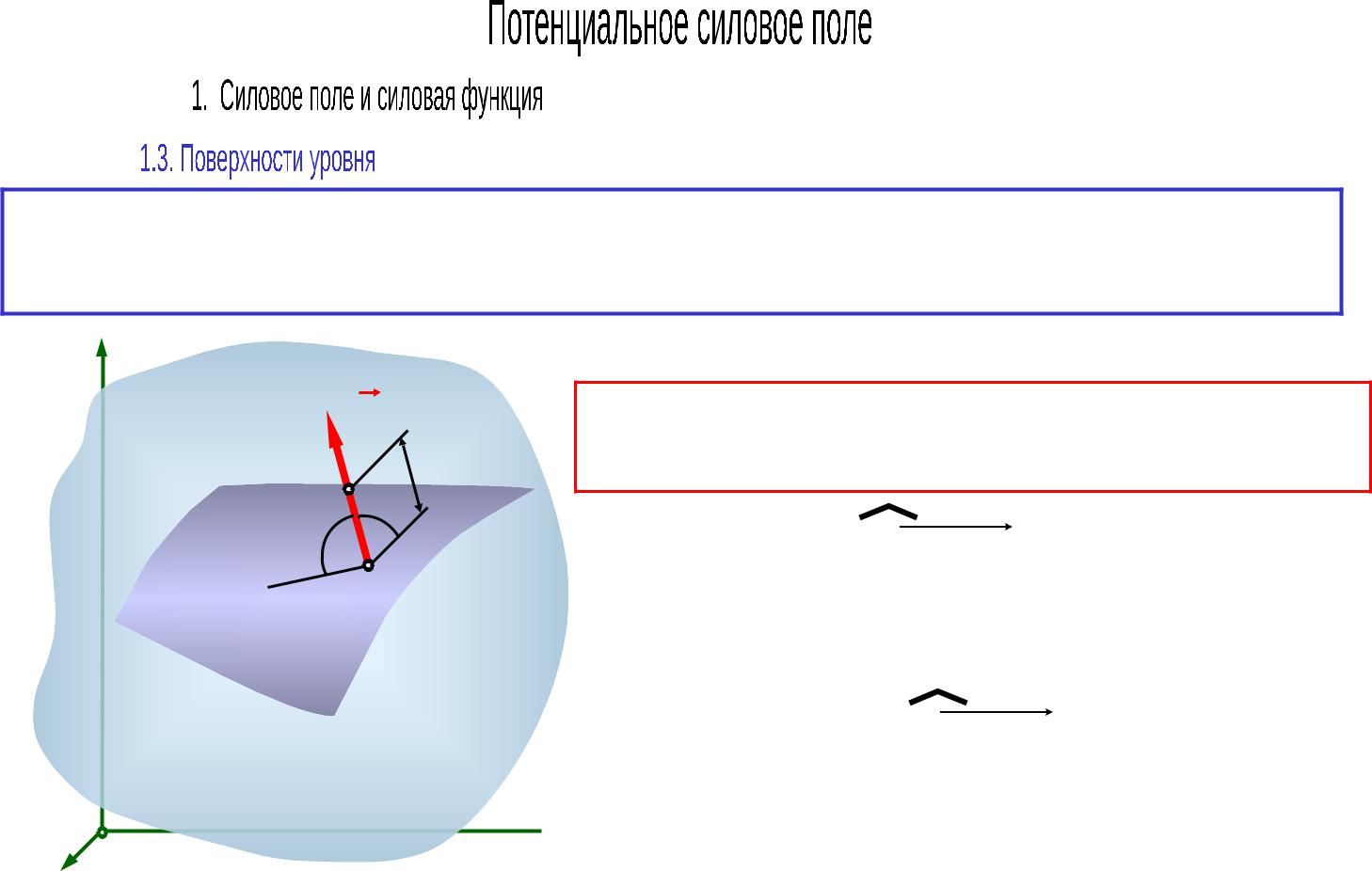
Свойства поверхностей уровня:
3.Сила в потенциальном силовом поле направлена в сторону возрастающих значений силовой функции.
F ds cos F , MM 1 C1 C 0,
так как C1 C .
cos F , MM 1 0;
y следовательно сила направлена в 
сторону возрастания U.
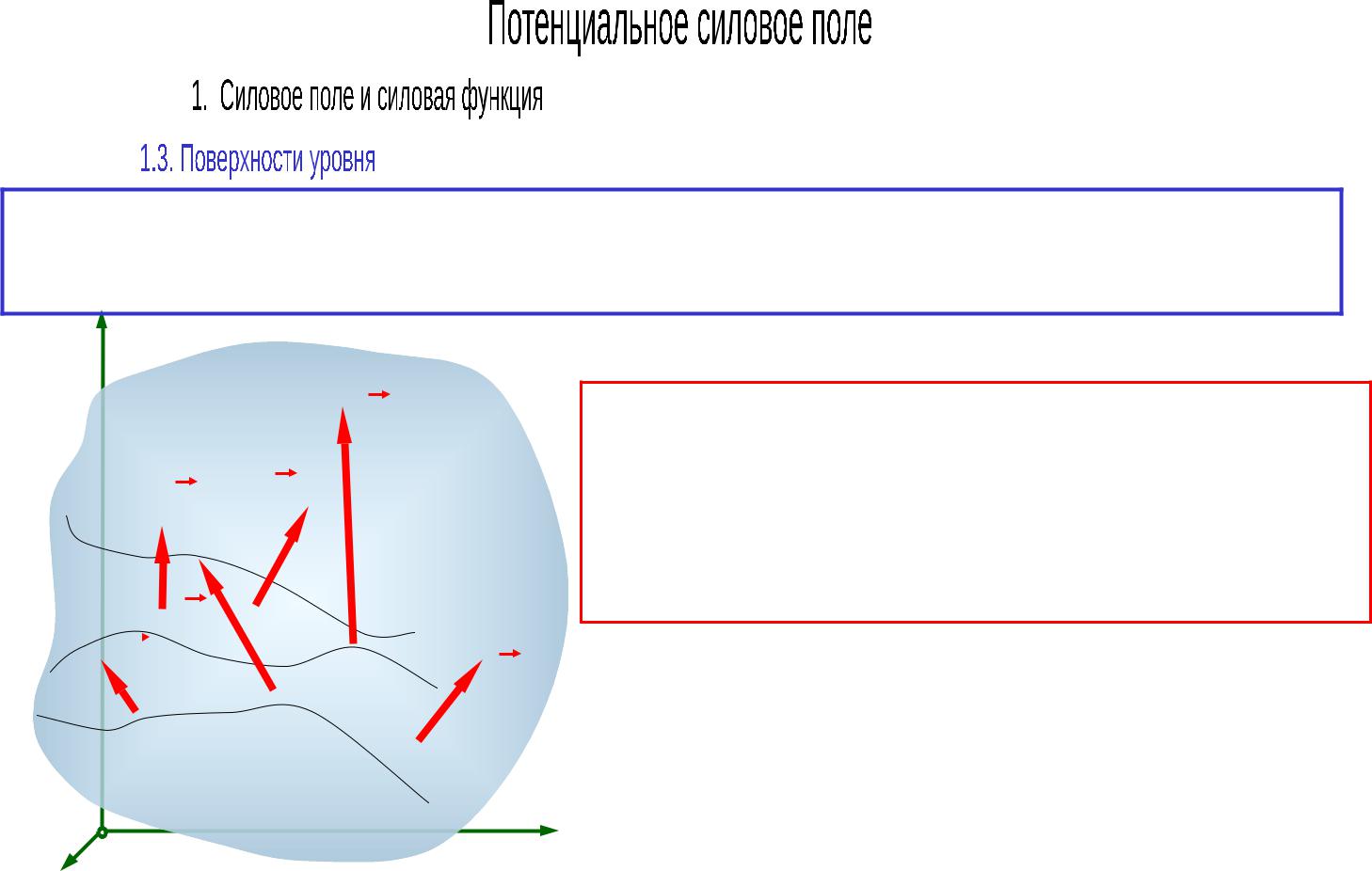
Точки потенциального силового поля, имеющие одинаковое значение силовой функции U=C, образуют поверхность, которую называют
поверхностью уровня
z
F1 F2
F5
F6
O
F3
|
|
|
|
|
U |
|
|
|
|
|
∆ |
|
|
|
|
|
+ |
|
|
|
|
|
U |
|
|
|
|
|
∆ |
|
|
|
|
|
+ |
|
|
|
|
|
|
U |
|
|
|
|
U |
F |
|
|
|
|
∆ |
||
|
|
|
|
|
||
|
|
|
U |
+ |
|
4 |
|
|
|
|
|
|
|
U
Свойства поверхностей уровня:
4.Если потенциальное силовое поле разбить на поверхности уровня, силовые функции которых отличаются друг от друга на одинаковую величину ∆U, то сила будет больше там, где поверхности уровня ближе друг к другу.
Работа силы на перемещении между двумя соседними поверхностями уровня одинакова во всех точках, следовательно сила будет больше там, где меньше
y расстояние.
x
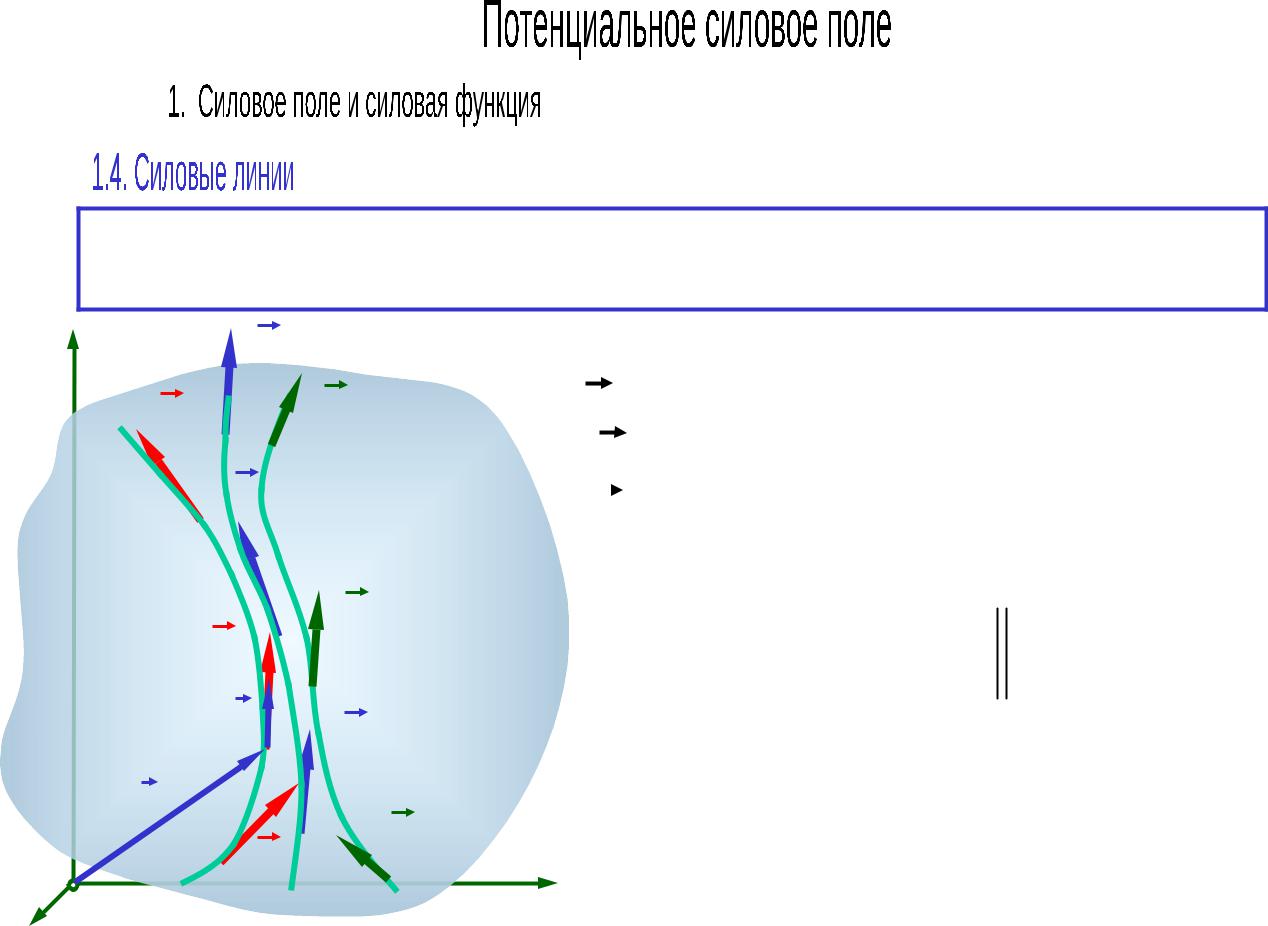
Линия, в каждой точке которой сила направлена по касательной к линии называется силовой линией
z |
|
Ф3 |
|
r – радиус-вектор точки; |
|||||
F |
3 |
|
P3 |
||||||
|
|
|
dr – дифференциал радиус-вектора точки; |
||||||
|
|
Ф2 |
|
||||||
|
|
|
dr |
направлен по касательной к кривой. |
|||||
|
|
|
|
||||||
|
|
F2 |
P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dr F |
||
|
|
dr |
Ф1 |
|
dx |
dy |
dz |
|
|
|
|
|
|
– дифференциальные |
|||||
|
|
|
P1 |
|
|||||
r |
|
|
|
F |
F |
|
F |
уравнения силовой |
|
O |
|
F1 |
|
y |
x |
|
y |
z |
линии. |
x
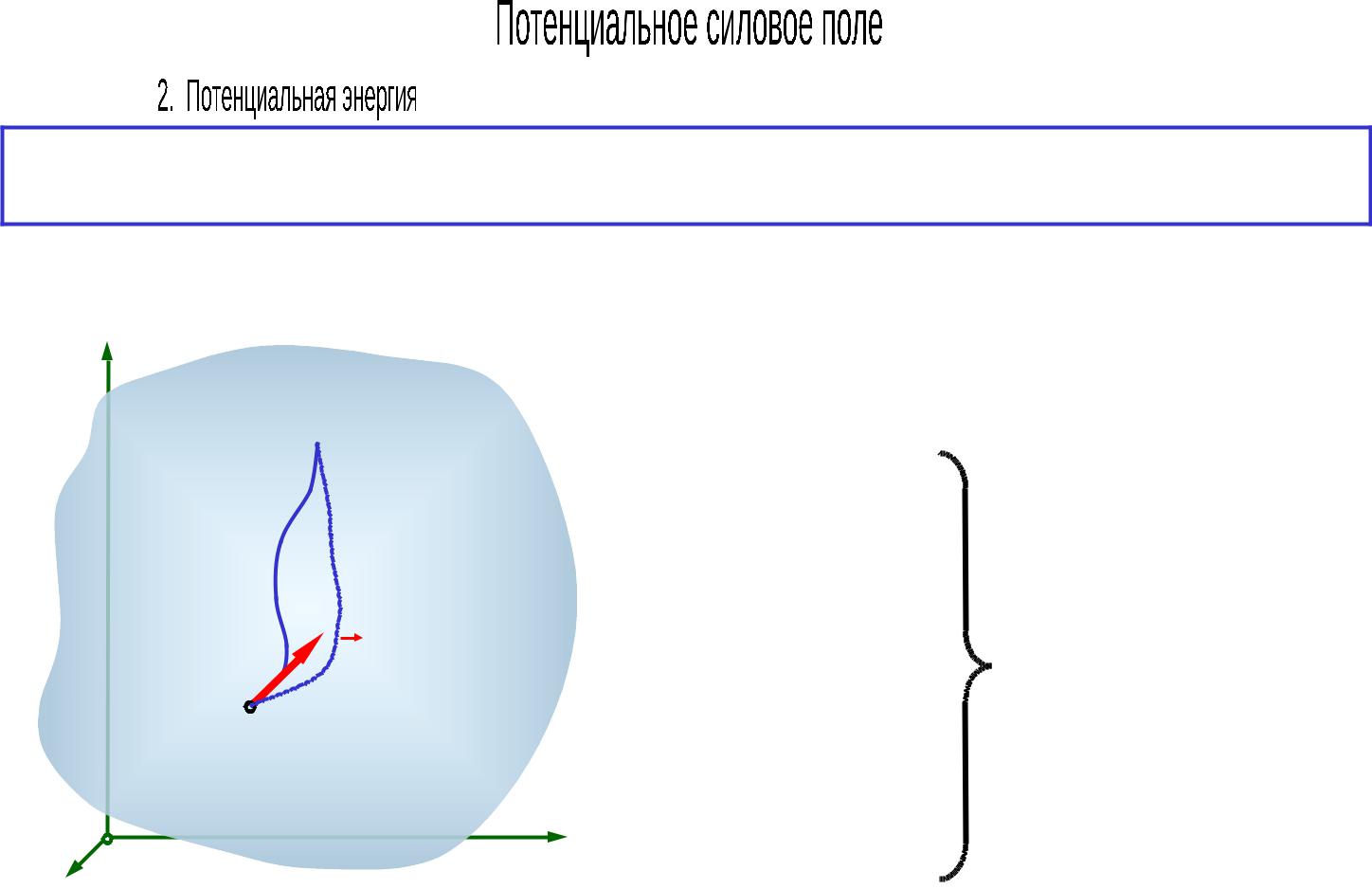
Функция потенциального силового поля, характеризующая запас энергии в данной точке поля называется потенциальной энергией
Потенциальная энергия П вычисляется как работа, которую совершают силы |
|
поля, действующие на точку при перемещении ее из текущего положения в |
|
начальное. |
П AMM0 ; или П U0 U C0 U; |
z |
|
|
U |
M(x,y,z) |
|
F U |
|||
|
П |
|
|||||
|
|
|
|
||||
|
|
|
|
x |
|
|
x |
|
|
F |
|
Fy |
|
U |
|
|
|
|
y |
||||
|
|
|
|
|
|
||
U0 = C0 |
M0(x0,y0,z0) |
|
|
|
|
||
O |
|
|
y |
Fz |
|
U |
|
|
|
|
z |
||||
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
П |
|
|
|
x |
dA dU dП; |
|
|
П |
||
A U U0 П0 П; |
|||
|
y |
||
|
П |
П U |
|
|
z |
|
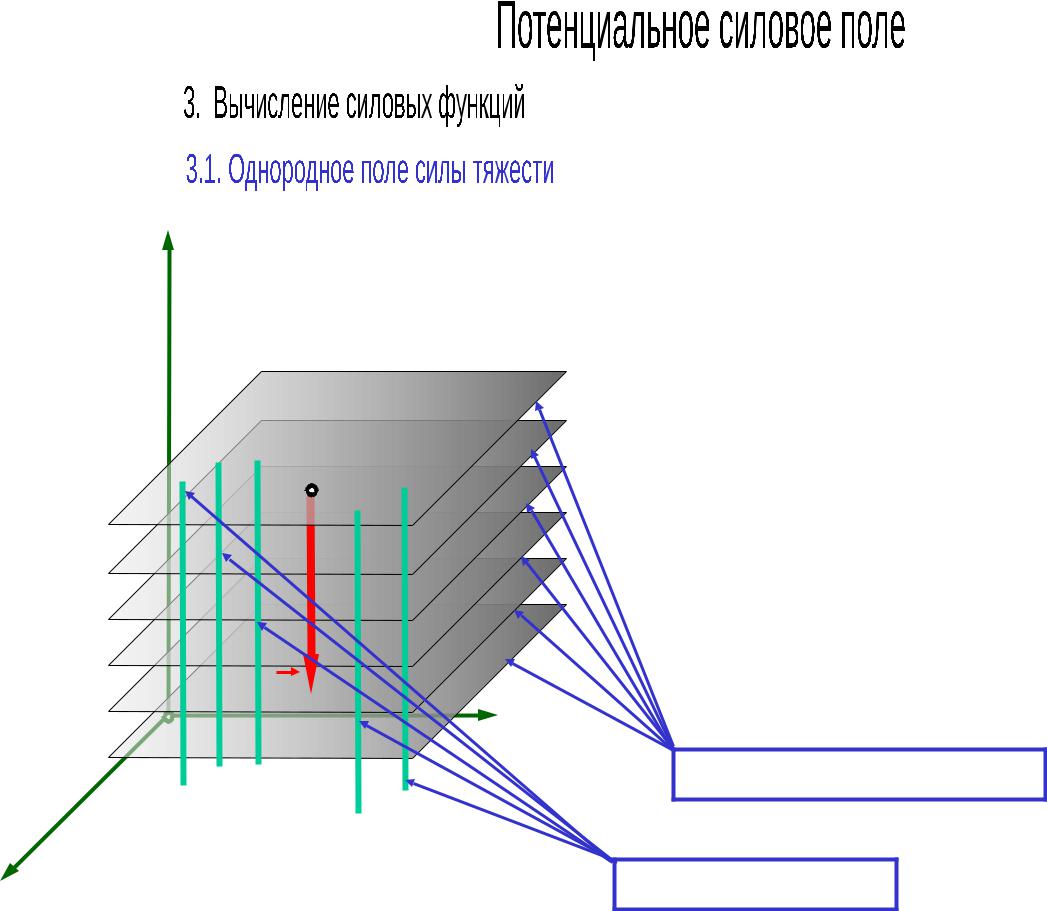
z
Px 0; Py 0; Pz mg.
|
dA Pxdx Pydy Pzdz |
M(x,y,z) |
mg dz d mgz . |
dU dA.
O
P
y
U mgz const.
Поверхности уровня
Силовые линии
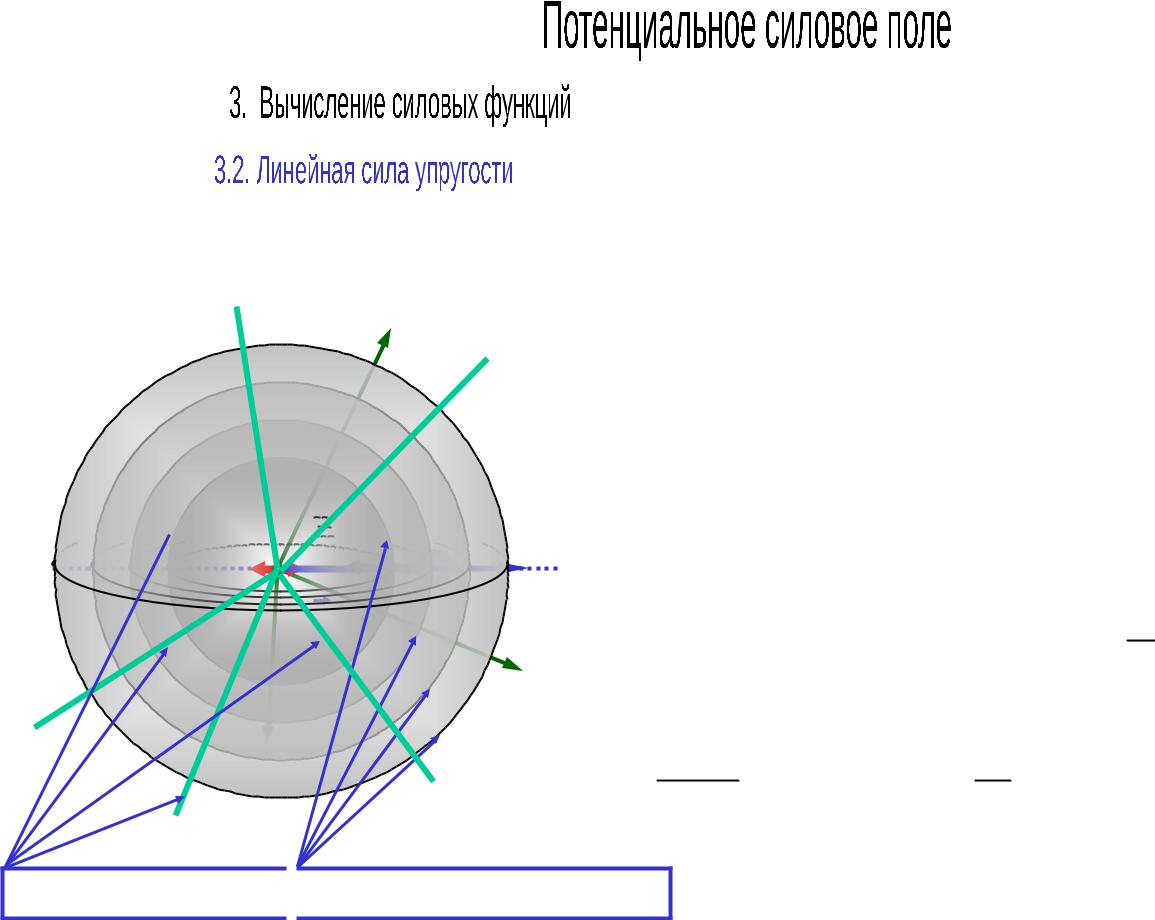
F
y
F
O r(t) r(t)
x
z
cr ; Fx cx; Fy cy; Fz cz.
dA Fxdx Fydy Fzdz
c xdx ydy zdz ;
rdr xdx ydy zdz; r2 x2 y2 z2 ;
dA cr dr 21 d cr2
U cr22 const 2c x2 y2 z2 const
Силовые линии 
Поверхности уровня
|
|
|
|
|
F |
k |
|
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
r |
; |
|
|
|
|
|
|
|
|
||||
r |
|
|
|
|
r o |
r |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ro F |
k |
|
|
|
|
k |
r |
|
k |
|
|
|||||||||||
|
F |
|
r o |
|
|
|
|
|
|
|
|
|
|
r . |
|
|
||||||
|
r2 |
r |
2 |
|
|
r3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||||||
F |
|
k |
|
x; F |
y |
|
k |
|
y; F |
k |
z. |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||
x |
|
r3 |
|
|
|
|
|
|
|
|
|
r3 |
|
z |
|
r3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||