
- •Кинетическим моментом точки относительно какого-либо центра называют момент количества движения точки относительно этого
- •Для материальной точки:
- •Разложим плоское движение на поступательно со скоростью центра масс и вращательное вокруг центра
- •Тележка D подъемного крана движется с постоянной скоростью и относительно стрелы ВС. Мотор,
- •Тележка D подъемного крана движется с постоянной скоростью и относительно стрелы ВС. Мотор,
- •По хорде MN диска радиуса r, вращающегося вокруг неподвижной вертикальной оси, движется груз
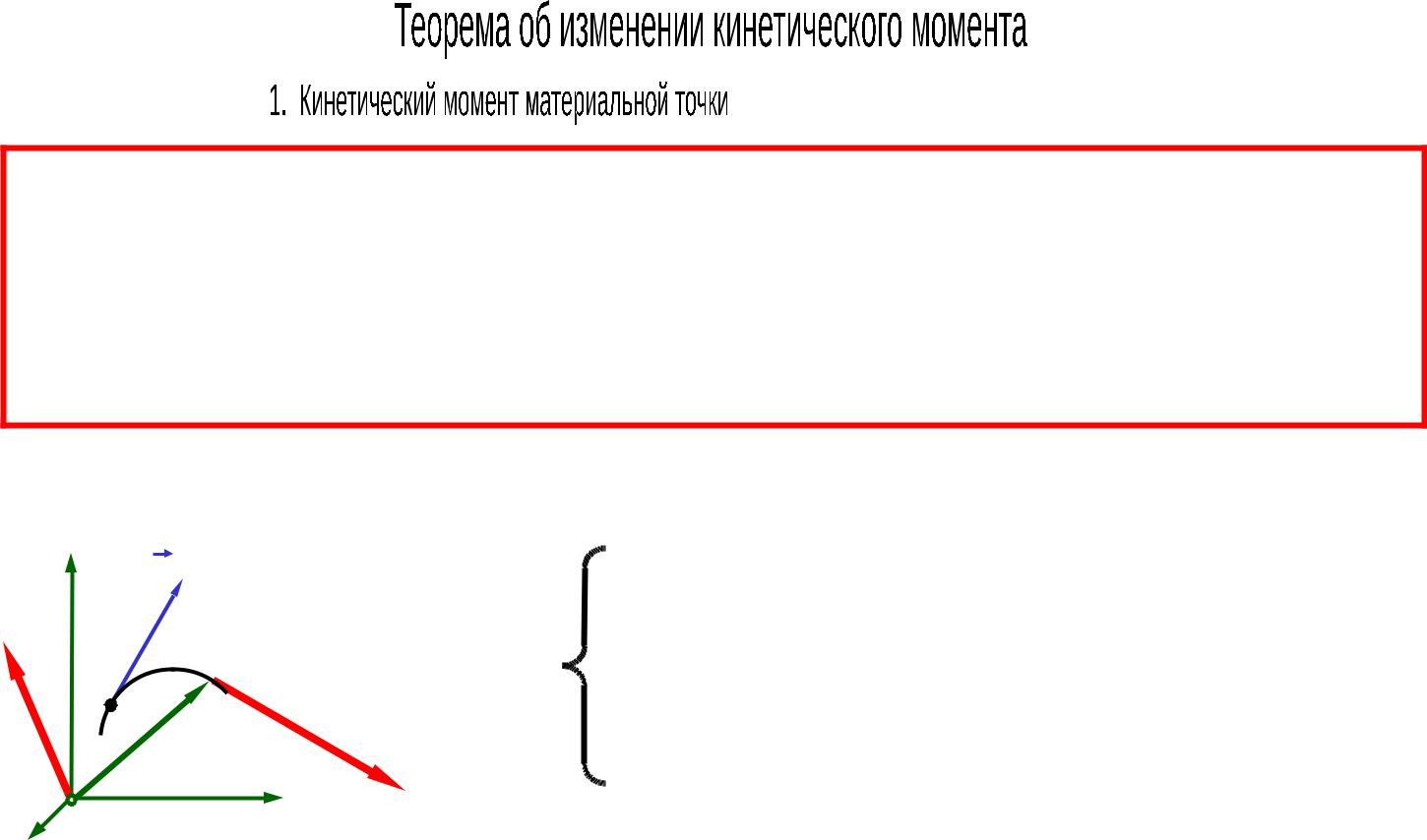
Кинетическим моментом точки относительно какого-либо центра называют момент количества движения точки относительно этого центра:
|
|
|
kO MO mv r |
mv |
|
В проекциях на координатные оси:
z |
v |
|
kOx Mx mv m yvz |
||||
kO |
|
|
|||||
m |
|
q mv |
kOy M y mv m zvx |
||||
|
r y |
kOz Mz mv m xvy |
|||||
O |
|
||||||
|
|
|
|
kOO |
|
|
|
|
|
|
|
r mv |
|||
|
|
|
Размерность: |
k |
|
||
|
|
|
|
м кг |
м |
||
|
|
|
|
|
|
|
с |
zvy ; xvz ; yvz .
н м с

|
|
|
||||||
|
Кинетическим моментом системы или главным моментом |
|
||||||
|
количества движения системы относительно какого-либо |
|
||||||
|
центра называется векторная сумма кинетических моментов |
|
||||||
|
точек этой системы относительно того же центра |
|
|
|||||
|
|
N |
N |
|
|
N |
|
|
|
KO kOk |
MO mkvk |
rk |
mkvk |
|
|||
|
|
k 1 |
k 1 |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
В проекциях на координатные оси:
KOx Mx mkvk mk ykvkz zkvky ; KOy My mkvk mk zkvkx xkvkz ; KOz Mz mkvk mk xkvky ykvkx .

z
 hk
hk mkvk
mkvk
|
|
M |
KO |
|
Kz |
ω |
rk |
|
|
|
|
|
|
y |
О
x
|
N |
|
Kz Mz mkvk ; vk hk ; |
||
|
k 1 |
|
Mz mkvk hkmkvk mkhk2 k ; |
||
|
N |
N |
Kz mk hk2 mkhk2 Jz |
||
|
k 1 |
k 1 |
Kz Jz
Кинетический момент тела относительно оси вращения равен произведению его угловой скорости на момент инерции относительно оси вращения
Kx Jxz , Ky J yz , где Jxz , Jyz – центробежные
моменты инерции.
Jxz J yz 0, Kx Ky 0, если Оz – главная ось
инерции тела для точки О.
z
k0 M0 m
r0 r
O
dkO
dt
mv0
M
y
MO F
|
|
m |
dv |
|
|
|
|
|
|
|
m |
dv |
|
|
|||
|
|
|
|
|
|
||||||||||||
ma F |
|
dt |
F |
r слева ; r |
dt |
r |
F ; |
||||||||||
|
dv |
|
d |
|
|
|
dr |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r m dt |
|
|
r |
mv |
dt |
mv ; |
|
|
|
|
|
||||||
dt |
|
|
|
|
|
||||||||||||
dr |
|
|
|
|
|
|
|
|
|
d |
|
|
|
||||
|
mv |
v mv 0; |
|
|
|
|
|
r mv r F ; |
|||||||||
dt |
|
|
|
dt |
|||||||||||||
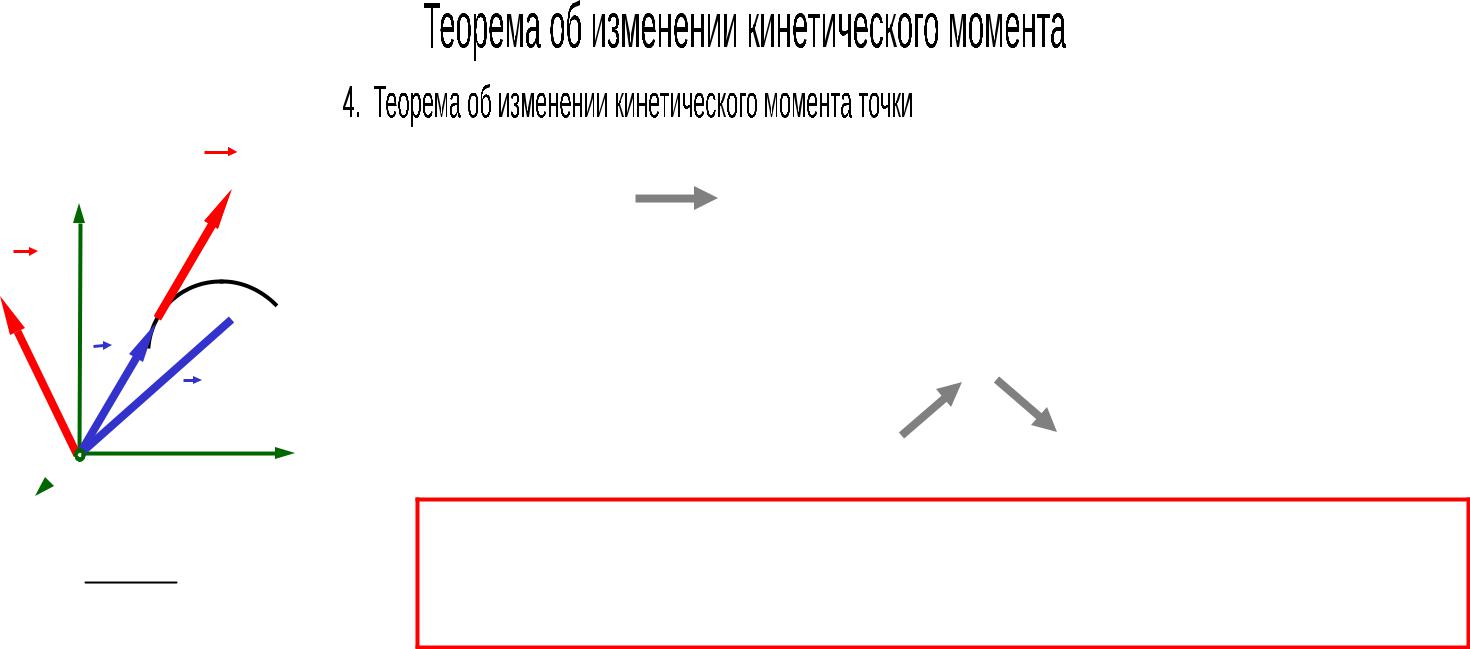
Производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра
В проекциях на координатные оси:
dkx |
|
|
dky |
|
|
|
|
|
Mx F |
; |
M y F |
; |
dkz Mz F |
. |
|||
|
||||||||
|
|
|||||||
dt |
|
dt |
|
dt |
|
|||

|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
rk mkvk rk |
Fk e rk |
Fk i , |
k 1, N ; |
|
|
|||||||||||||
|
|
|
|
|
dt |
|
|
||||||||||||||||||
|
d |
|
N |
|
|
|
|
N |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
N |
|
|||||||||||||
|
|
|
|
rk mkvk |
rk Fk e |
|
|
rk Fk i |
; |
|
|
|
rk Fk i 0 ; |
||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|
|
k 1 |
|
|
|
||||
|
|
|
|
N |
|
|
|
|
|
N |
|
|
N |
|
|
||||||||||
|
|
|
|
|
rk mkvk KO ; MO MO Fk e |
rk Fk e ; |
|||||||||||||||||||
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
k 1 |
|
|
|
|
||||
dKO |
|
|
e |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Производная |
по |
времени |
от |
кинетического момента |
|
|||||||||||||||||
|
|
|
MO |
|
|
|
системы относительно какого-либо центра равна главному |
|
|||||||||||||||||
dt |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
моменту внешних сил относительно того же центра |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В проекциях на координатные оси:
dKx |
MOxe ; |
dK y |
MOye ; |
dKz |
MOze . |
|
|
|
|||
dt |
dt |
dt |
|||
Для материальной точки: |
|
|
|
|
||
|
|
Если момент силы, приложенной к материальной точке |
||||
Если MO F 0,то dkO |
|
|
равен нулю, то кинетический момент точки постоянен |
|||
0; |
|
kO const |
||||
dt |
|
|
|
|
||
|
|
|
|
|
||
Для механической системы: |
|
|
Если главный момент всех внешних сил, приложенных к системе, |
|
||
|
|
равен нулю, то кинетический момент системы постоянен |
|
|||
ЕслиMOe 0,то dKO |
|
|
|
|
|
|
|
|
|
|
|
||
0; |
|
KO const |
||||
dt |
|
|
|
|
||
проекциях на координатные оси:
Для материальной точки: Для механической системы:
Если Mx F 0 |
, то kx const; |
Если Mxe |
0, то Kx const; |
|
||
My F 0 |
, |
ky const; |
e |
0, |
Ky const; |
Для тела, вращаю- |
My |
щегося вокруг оси Oz: |
|||||
Mz F 0, |
kz const; |
Mze |
0, |
Kz const; |
Jz Jz0 0 |
|
F1(e)
RA 

x
z |
|
|
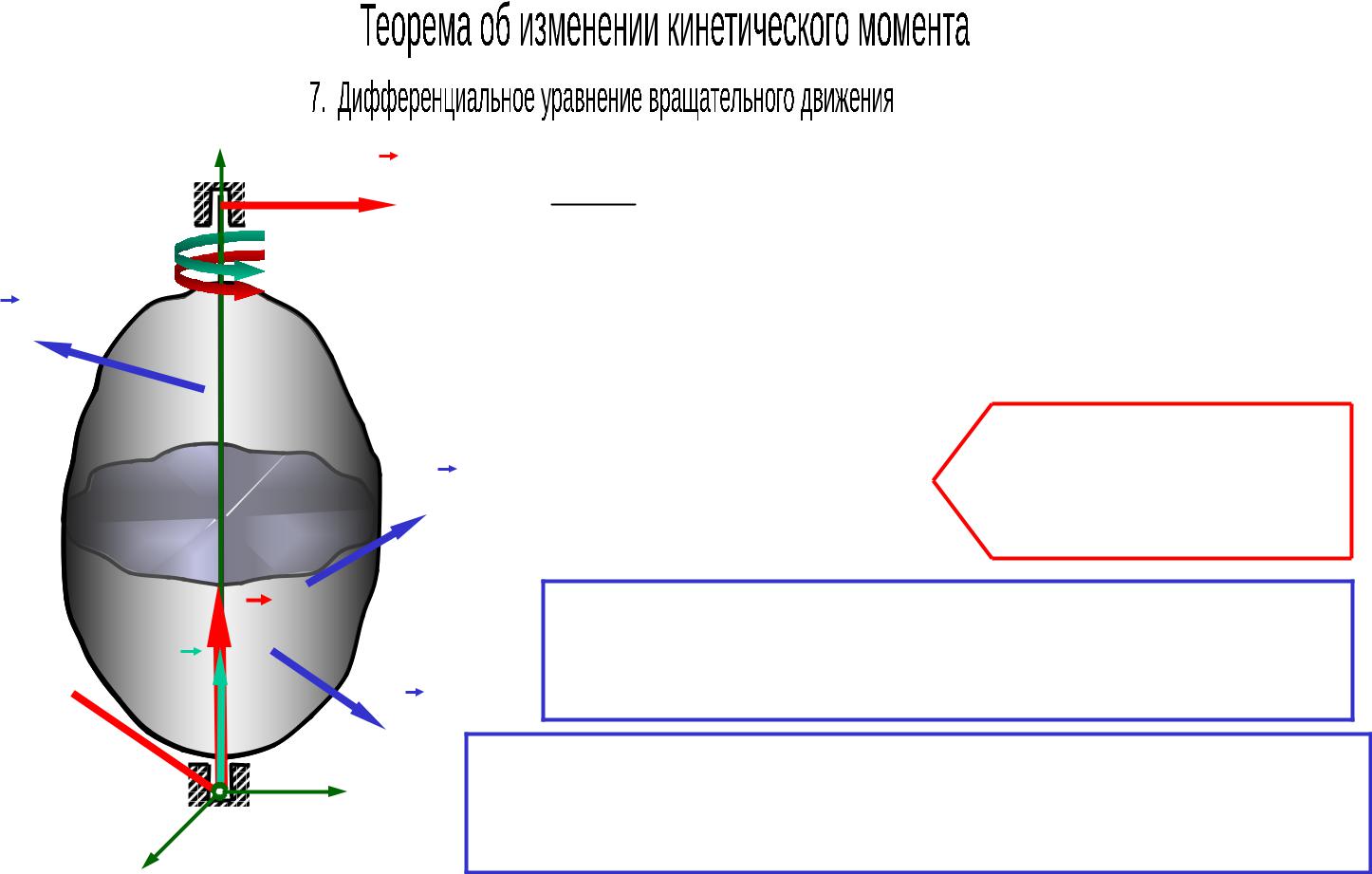
dKz |
|
|
n |
|
|
|
|
; |
Kz Jz ; |
|||
|
B |
RB |
Mz Fk e |
||||||||||||
|
|
|
|
dt |
|
k 1 |
|
|
|
|
|
e |
|
||
|
ε |
|
|
|
Jz |
d |
|
n |
|
|
; |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
dt |
|
Mz Fk |
||||||||
|
|
|
|
|
|
|
|
|
|
k 1 |
|
Дифференциальное |
|||
|
|
|
|
|
|
n |
|
|
e |
|
|
||||
|
|
(e) |
|
|
|
|
|
|
|
|
уравнение |
||||
|
|
F2 |
|
|
|
|
|
|
|
|
|
вращательного |
|||
|
|
Jz Mz Fk |
|
||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
движения |
||||
|
ε |
|
|
n |
|
|
|
e |
|
|
e |
const , |
const |
||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Если |
Mz Fk |
Mz |
|
|||||||||
ω |
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
F(e) |
|
k 1 |
Равнопеременное вращение |
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
e |
|
|
|
|
|
|||
|
|
Если |
|
|
|
|
|
то |
|
||||||
|
A |
|
Mz Fk |
|
Mz |
0 , |
|
0, const |
|||||||
|
|
k 1 |
|
Равномерное вращение |
|
||||||||||
|
|
|
|
|
|||||||||||
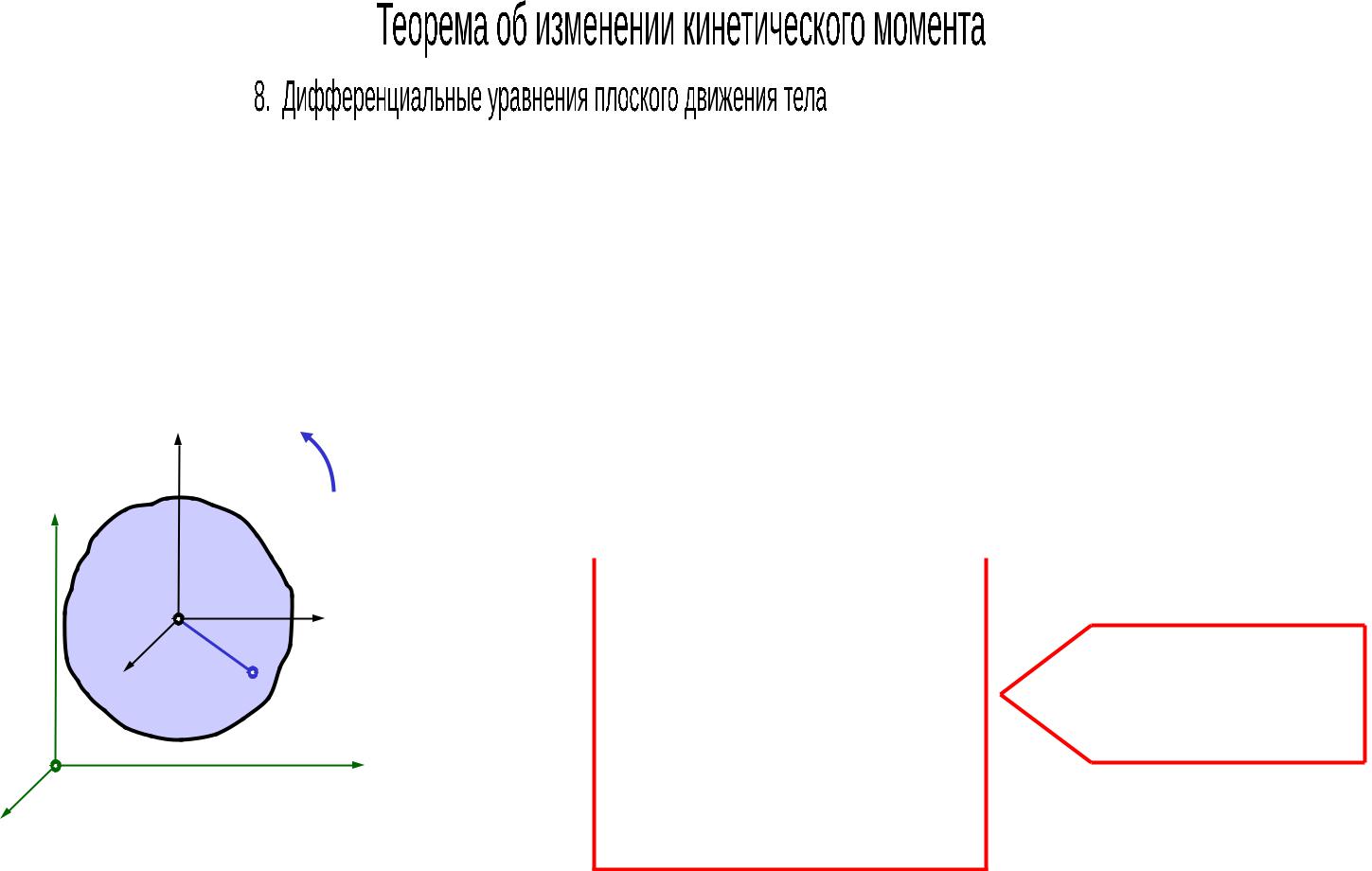
Разложим плоское движение на поступательно со скоростью центра масс и вращательное вокруг центра масс.
z1 |
φ |
|
z
С y1
x1
Мk
y
O
По теореме о движении центра масс для поступательной части |
|||||||
движения: |
n |
e |
|
n |
e |
|
|
|
, |
; |
|||||
|
|
||||||
MxC Fkx |
MyC Fky |
||||||
По теореме об |
k 1 |
|
|
k 1 |
|
|
|
изменении кинетического момента в |
|||||||
относительном движении вокруг центра масс: |
|
|
|||||
r |
n |
|
|
|
dKCz |
MCz Fk e , |
|||
dt |
k 1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
MxC |
Fkxe |
|
||
|
k 1 |
|
|
|
|
n |
e |
|
|
|
|
|||
MyC |
Fky |
|
|
|
|
k 1 |
|
e |
|
|
n |
|
|
|
|
|
|||
JCz MCz Fk |
||||
k 1
KCzr JCz JCz ;
Дифференциальные уравнения плоского движения тела
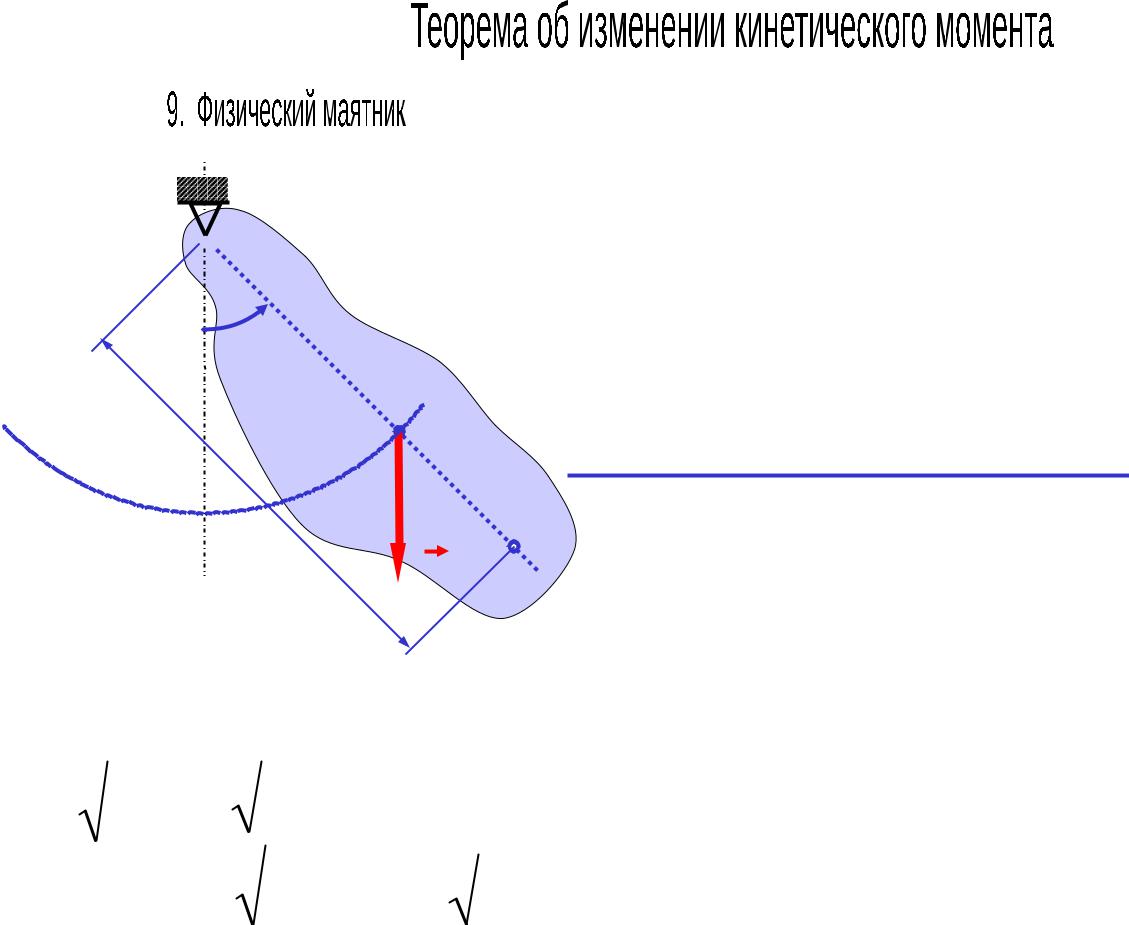
O
φ h |
|
|
|
|
С |
|
l |
O1 |
|
P |
||
|
|
|
n |
e |
; JOz Phsin ; |
||
|
|
|||||
|
JOz MOz Fi |
|
||||
|
|
i 1 |
|
|
|
|
|
Mgh |
sin 0 |
– |
дифференциальное |
уравнение |
|
|
движения физического маятника – |
|||||
|
|
|
||||
|
JOz |
|
|
не интегрируется в элементарных |
||
|
|
|
функциях. |
|
||
В случае малых колебаний ( sinφ ≈ φ ): Mgh 0
J\Oz
Общее решение дифференциального |
Asin kt |
||
уравнения |
малых |
колебаний |
|
физического маятника : |
|
||
l |
JOz |
|
|
– приведённая длина физического маятника; |
O |
– |
точка привеса; |
||||||||||||||
Mh |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
– |
центр качаний; |
|
k |
Mgh |
|
g |
|
|
|
|
|
|
|
|
||||||||||
|
JOz |
|
|
|
– |
|
круговая частота колебаний; |
A1 |
|
|
|||||||||||
|
|
l |
– |
амплитуда колебаний; |
|||||||||||||||||
|
|
2 |
|
|
|
|
|
JOz |
|
|
|
|
|
|
|
|
|||||
T |
|
2 |
|
|
2 |
l |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
– период малых колебаний. |
– |
начальная фаза колебаний; |
|||||||||||
k |
|
|
Mgh |
g |
|||||||||||||||||

|
|
|
|
|
|
|||||||||||
|
|
Приведенная длина физического маятника больше расстояния от точки |
||||||||||||||
|
привеса до центра масс – |
l > h . |
|
|
|
|
||||||||||
|
Применяя теорему Штейнера получим: |
|
|
|
|
|
||||||||||
l |
J |
Oz |
|
J |
Cz |
Mh2 |
|
J |
Cz |
|
h h, так как O1C |
J |
Cz |
|
l h 0. |
|
|
|
|
Mh |
Mh |
Mh |
|||||||||||
|
|
Mh |
|
|
|
|
|
|||||||||
Центр качаний и точка привеса обратимы (взаимозаменяемы).
Если то же тело подвесить за ось, проходящую через центр качаний параллельно первоначальной оси, то приведенная длина полученного нового физического маятника будет равна приведенной длине
|
|
старого l1 = l . |
|
|
|
|
|
||||
|
Применяя теорему Штейнера получим: |
|
|
|
|
|
|||||
l1 |
|
JO z |
|
J |
Cz |
M l h 2 |
|
J |
Cz |
l h l, так как JCz Mh l h . |
|
1 |
|
|
|
||||||||
M O1C |
|
|
M l h |
M l h |
|||||||
|
|
|
|
|
|
|
|
||||
