Добавил:

Limyr1201 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ростовский Государственный Университет Путей Сообщения

Предмет:

Теоретическая механика

Файл:

Лекции / SKD_Lektsia_13_new_-_Dinamika_sistemy_Geometria_mass_Kol-vo_dvizhenia_Dvizhenie_TsM.pptx

Скачиваний:

Добавлен:

19.09.2024

Размер:

489.79 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

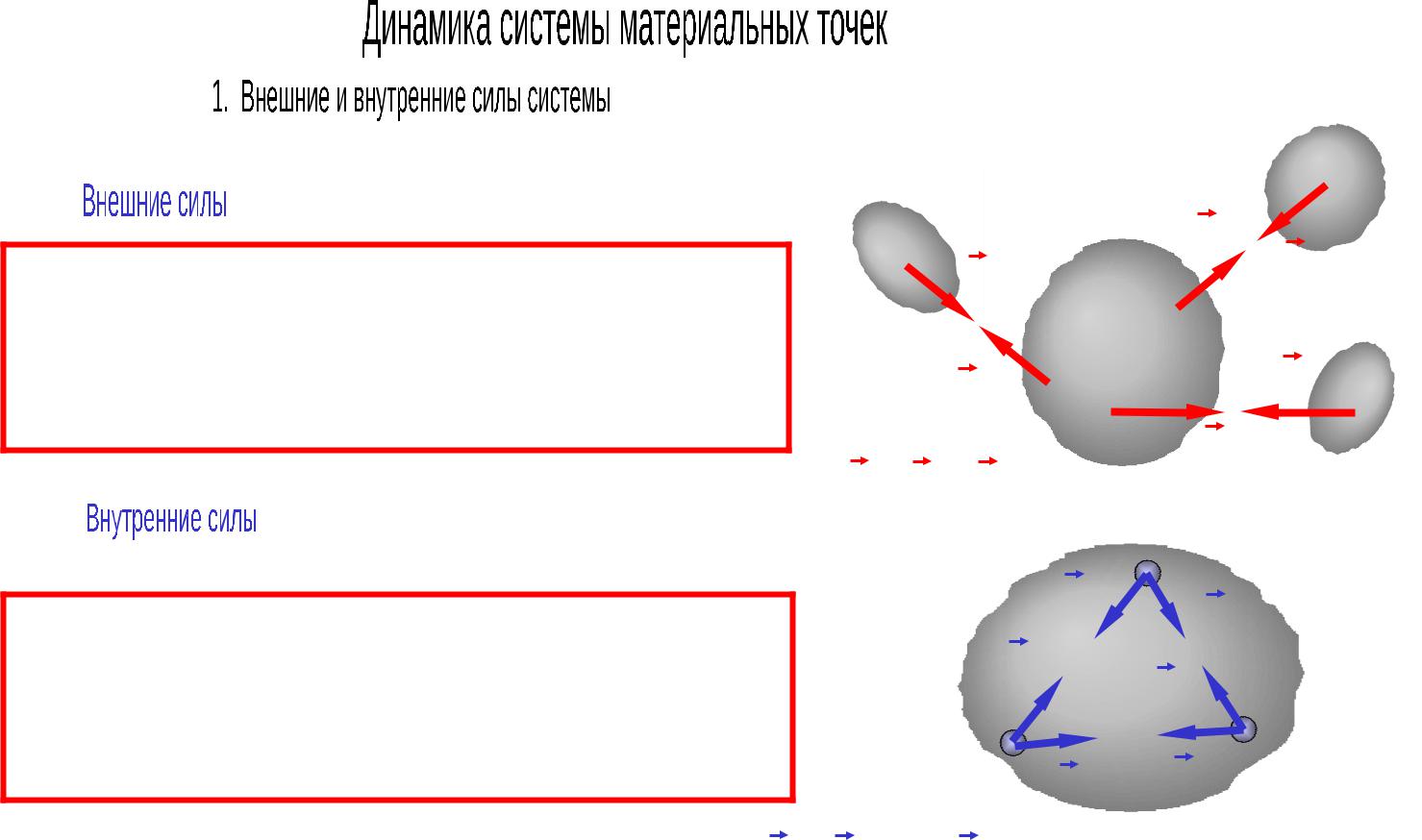
Внешними силами механической системы называют силы, действующие на систему со стороны механических объектов, не входящих в систему

	F(e)
Fn'	1	F1'
		F1'

Fn(e)

F1(e),F2(e),Fn(e)

Рассматриваемая

механическая система F2'

F2(e)

– внешние силы системы

Внутренними силами механической системы называют силы взаимодействия между точками и телами системы

	F(i)		m2
	F(i)		(i)
	21	F2n
	21
F(i)		Fn2(i)	mn
12		Fn2(i)	mn
12

m1F1n(i) Fn1(i)

F12(i) ,F21(i), … ,Fn1(i) – внутренние силы системы



еорема:		Главный вектор всех внутренних сил системы и главный момент
		этих сил относительно любой точки равны нулю при любом
		состоянии системы

		F2(i)	M2	F1(i)	F2(i)	M
		F2(i)	M2	F1(i)		2
						2
F (i)				M1
M1	1				h
					h
				r1		r2

Fk(i)

e F i ;

1 dt2

;

F i

dt2

(xk , yk , zk)

В проекциях. .на. .координатные. . . . . . . . . .оси:.

;

2dx rk

F e

F i

F ek

F ik

;

F(e)

dt2

. . . . . . . . . . . . . . .

2 y2

N kyF

kyF

; k 1, N

dt dt

d 2 zk

;

d rk

, k 1,N

dt2

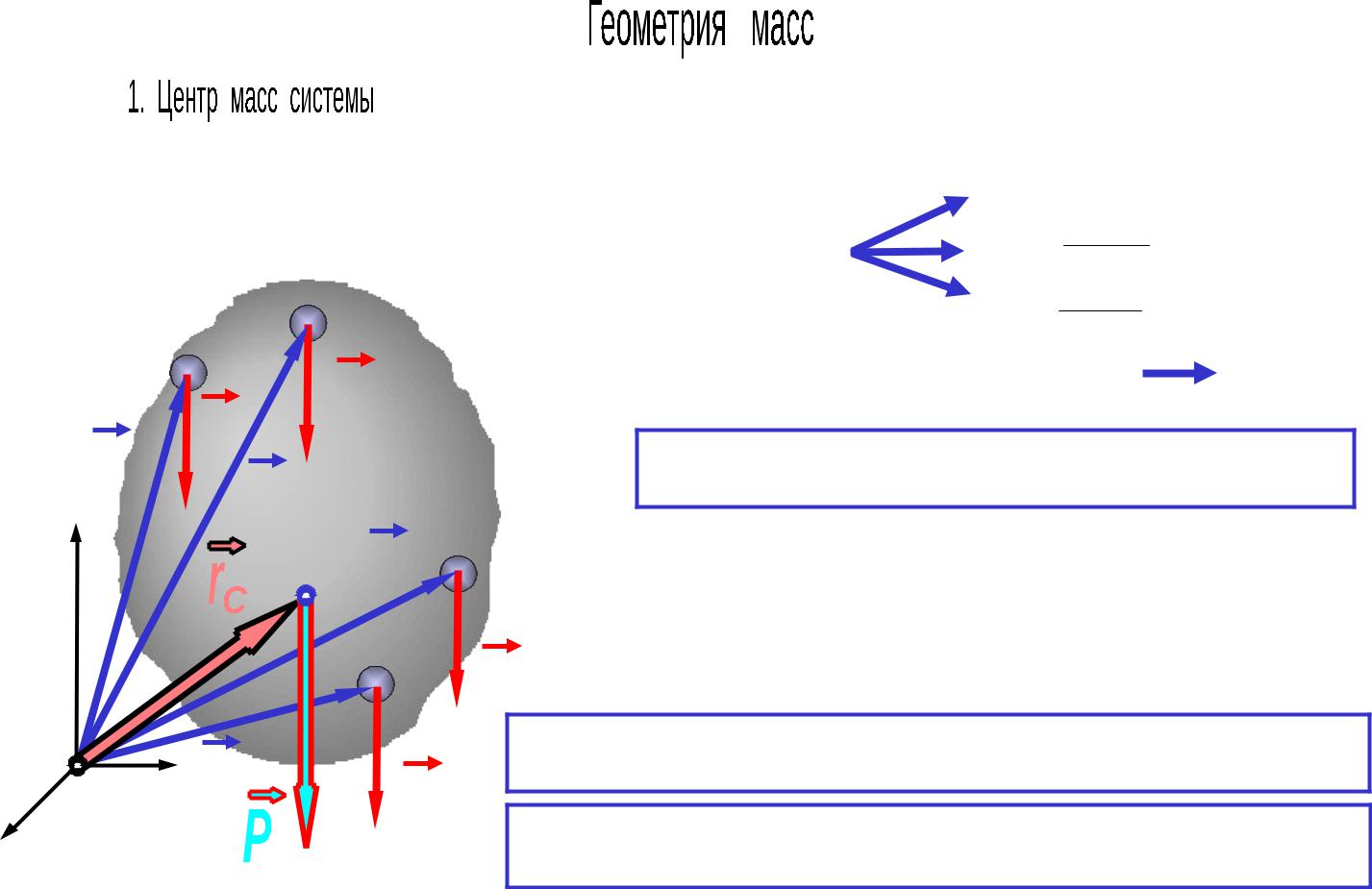
m1 ,m2 ,...,mi ,...,mn ;

M mi ;

mi xi

;

r1 ,r2 ,...,ri ,...,rn ;

mi yi

Координаты

miri

Радиус-вектор центра масс системы:

центра масс

;

системы:

mi zi

Pi mi g;P Pi ;

P r

В поле силы тяжести:

r i i

Статический момент системы

относительно полюса О:miri MrC ;

Статические моменты системы

yOz – m x Mx ;

относительно плоскостей:

xOz –mi yi

MyC;

i i

xOy –mi zi

MzC .

Статический момент системы относительно

y n

центра масс равен НУЛЮ: M C

Статические моменты системы относительно ЛЮБОЙ

плоскости, проходящей через центр масс равны НУЛЮ

m1	Z r2			m2
m1				m2
	1
r	1	r2	z2		mi
	1	r2	r
			r	i
				i
1			ri
O rn			ri		m
O rn					m
			rn		zni
	O		rn

Величины, характеризующие распределение масс системы относительно точки (центра), оси, плоскости, выражающиеся через суммы произведений масс точек на квадраты их расстояний до точки (центра), оси, плоскости называются МОМЕНТАМИ ИНЕРЦИИ СИСТЕМЫ относительно точки (центра), оси или плоскости

JO m–iriмомент2 инерции системы относительно центра О;

i 1 n

JZ m–iriмомент2 инерции системы относительно оси Z;

	i 1
		n
JxOy m–i ziмомент2						инерции системы относительно плоскости xOy;
	i 1						Моменты инерции твердого тела:
	i 1
J			n				r2dm
J	O		r2		m		r2dm
	O	lim	i			i		– относительно центра О;
y		mi 0	i 1				M
y
	z		n
J	z	lim	i	2		i		2dm– относительно оси Z;
J			r	2		m	r	2dm– относительно оси Z;
		mi 0 i 1					M

mi 0

i 1

кгi 1

mмr

lim

азмерность:

– относительно плоскости xOy;

i i

Момент инерции тела относительно оси часто представляют как произведение массы тела на квадрат некоторого расстояния: JZ M z2 ;

Это расстояние	z	Jz	,

		M	называют РАДИУС ИНЕРЦИИ ТЕЛА относительно оси.
Радиус инерции реальных тел определяют по специальным справочникам.

JOz JCz Md2

Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс системы, плюс произведение массы системы на квадрат расстояния между осями

Количеством движения материальной точки называют вектор, равный произведению массы точки на ее скорость:

qmv

Впроекциях на координатные оси:

	v		qx mvx mx;
z
			qy mvy my;

	m		qz mvz mz.
	m
		y	q mv	qq
x O		y			mv
			Размерность:		mv
			Размерность:		кг м
					с

Количеством движения системы называют векторную сумму количеств движения точек, входящих в систему:

	N	N
Q	qk mkvk
	k 1	k 1

В проекциях на координатные оси:

Qx qxk k 1

Qy qyk k 1

Qz qzk k 1

mkvxk k 1

mkvyk k 1

mkvzk k 1

mk xk

k 1

mk yk

k 1

mk zk

k 1

Вычисление количества движения системы:

Q mkvk mk k

mkrk

;

k 1

dt k 1

k k

m r

r ;

– радиус вектор центра масс системы

k 1

Q M

M v

Количество движения системы равно произведению массы системы на скорость центра масс

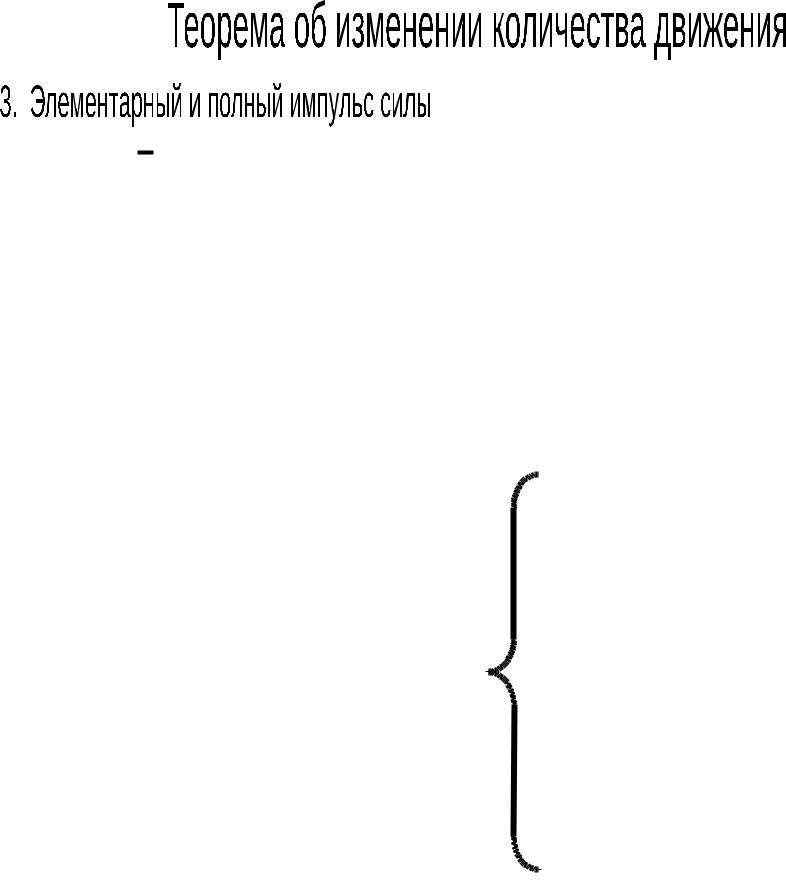
Действие силы F на материальную точку в течении времени dt можно охарактеризовать элементарным импульсом силы:

dS F dt

олный импульс силы:

S F dt

Размерность ( СИ ):

dS FH dtc

В проекциях на координатные оси:

Sx Fx dt;

0 t

Sy Fy dt;

0 t

Sz Fz dt;

mv0

ma F ;

F ;

В проекциях на координатные оси:

mv F

– теорема об изменении количества

движения точки в дифференци-

mvx mv0 x

Sx ;

альной форме

Sy ;

d mv Fdt;

mv0 y

dmvyv dS

альной форме

– теорема импульсов в дифференци-

;

Fdt;

0 z

об изменении

d mv

mv mv

S – теорема

количества движения точки

в конечной форме

Изменение количества движения точки равно полному импульсу силы, действующей на точку за период изменения

mv F

– теорема об изменении количества движения точки в дифференциальной форме.

, k 1, N .

Для системы из N материальных точек:

mkvk Fk

N i

Суммируя по всем точкам системы:

mkvk Fk

dt k 1

k 1

mkvk

Q ;

Fk i 0 .

k 1

Теорема об изменении количества движения системы в дифференциальной форме:

dQ	N
dQ	Fk e
dt	k 1

Теорема об изменении импульсов системы в дифференциальной форме:

	N		N
dQ Fk e dt ;		dQ	dSke ;
	k 1		k 1

N Sk

dQ dSke ;

Интегрируя обе части:

dQ dSke ;

k 1

k 1 0

– теорема об

изменении

Q Q0

количества

движения

Или: Q

k 1

системы в конечной форме.

k 1 0

Изменение количества движения системы равно суммарному полному импульсу всех внешних сил, действующих на систему за период изменения

N
Qx Q0 x Skxe ;
k 1
N
В проекциях на координатные оси: Qy Q0 y Skye	;

k 1

Qz Q0 z Skze . k 1

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции

#
19.09.2024506.27 Кб3SKD_Lektsia_08_-_Kinematika_tela_postupatelnoe_vraschatelnoe_dvizhenie.pptx
#
19.09.20241.63 Mб3SKD_Lektsia_09_new_-_Kinematika_tela_ploskoe_dvizhenie.pptx
#
19.09.2024599.58 Кб3SKD_Lektsia_10_-_Slozhnye_dvizhenia_tochki.pptx
#
19.09.2024471.21 Кб3SKD_Lektsia_11_-_Osnovnye_opredelenia_axiomy_difuravnenia_dvizhenia_tochki.pptx
#
19.09.20241.48 Mб3SKD_Lektsia_12_-_Kolebania_materialnoy_tochki.pptx
#
19.09.2024489.79 Кб3SKD_Lektsia_13_new_-_Dinamika_sistemy_Geometria_mass_Kol-vo_dvizhenia_Dvizhenie_TsM.pptx
#
19.09.2024553.87 Кб3SKD_Lektsia_14_-_Teorema_ob_izmenenii_kineticheskogo_momenta.pptx
#
19.09.20245.1 Mб3SKD_Lektsia_15_-_Teorema_ob_izmenenii_kineticheskoy_energii.pptx
#
19.09.2024429.85 Кб3SKD_Lektsia_16_-_Potentsialnoe_silovoe_pole_Zakon_sokhranenia_energii.pptx
#
19.09.20242.43 Mб3SKD_Lektsia_17_new_-_Osnovnye_ponyatia_analiticheskoy_mekhaniki.pptx